【機械設計マスターへの道】管路における圧力損失［流体力学の基礎知識④］

Tweet

Pocket

様々な流体を遠方へ移送するために配管が利用されます。配管内の流体の通り道を「管路」といいます。

管路内を流体が流れる際、流体の粘性による摩擦のために圧力損失が生じます。
このため、液体であればポンプ、気体であれば送風機や圧縮機などの流体機械を使用して、圧力損失を補うだけの圧力エネルギーを流体に与える必要があります。

１．層流、乱流、レイノルズ数

断面形状が円の管路（円管）内に非圧縮性流体を流す場合、流速が遅いとき、流れは乱れることなく真っすぐに直線状の筋を描いて流れます。このような流れを「層流」といいます。

流速が大きくなると、流れは流れ方向以外の速度成分を持つようになり、渦を生じて乱れた状態になります。このような流れを「乱流」といいます。

1883年レイノルズは、図１のような流れの可視可装置を考案製作して、水温、管径、流速を変えて実験を行い、層流から乱流に変化する現象（遷移）は、次式で示す無次元数Reにより判別されることを発見しました。

　Re = vd/ν　　・・・（1）
ここに、ｖ：流速(m/s)、d:管内径(m)、ν：動粘度(m²/s)
この無次元数Reを「レイノルズ数」といいます。

レイノルズ数は、流れの慣性力と粘性力の比を示す数値です。
流速が小さいと粘性力が支配的となって流れは層流となりレイノルズ数は小さくなります。流速が大きくなると慣性力が支配的となって流れは乱流となりレイノルズ数は大きくなります。

層流から乱流への遷移が起きるときのレイノルズ数を臨界レイノルズ数Recといい、円管内の流れにおいてRecは約2320になります。
実際には、層流から乱流への遷移と乱流から層流への遷移とでRecは異なり、入り口部の流動状態などにも影響され、層流、乱流の遷移域は2100< Rec<4000程度の範囲となります。

【図1　レイノルズの実験】

２．直管における摩擦損失

内直径d(m)、長さL(m)の直管内を流速v(m/s)で流体が流れるときに生じる損失ヘッドh_L(m)を次の式で計算することができます。

　h_L＝λ(L/d)(v²/2g)　　・・・(2)
　［ g：重力加速度(m/s²),　λ：管摩擦係数（無次元）］

（2）式を、ダルシ―・ワイスバッハの式といい、層流・乱流にかかわらず、粘性による摩擦損失を計算する公式として適用することができます。
管摩擦係数λは、流れが層流の場合と乱流の場合で異なります。
 

《層流の場合》

　λ=64/ Re　　・・・(3)
上式で表され、λはレイノルズ数Reに反比例する関数となります。
 

《乱流の場合》

壁面が滑らかな場合は、λがReの関数となるいくつかの実験式があります。
ただし適用できるRe の範囲があるので注意が必要です。
 

① ブラジウスの式（Re =3×10³～1×10⁵）

　λ=0.3164/ Re^0.25　　・・・(4)-1
 

② ニクラゼの式（Re =1×10⁶～3×10⁶）

　λ=0.0032+0.221 Re^-0.237　　・・・(4)-2
 

③ カルマン・プラントルの式

　1/√λ=2.0log(Re √λ)-0.8　　・・・(4)-3
この式は、広範囲のReで実験結果と適合しますが、λがReの単純な関数とならないので、取り扱いは難しくなります。
 

管内壁面の粗さが無視できない大きさである場合は、相対粗さε/dの関数として管摩擦係数λを取り扱う必要があります。相対粗さとは、管の内直径dに対する、壁面の平均粗さεの比のことです。
各種の実験結果からは、あるレイノルズ数を超えると管摩擦係数λはレイノルズ数によらず、相対粗さε/dごとに一定値となる傾向を示します。

　λ=1/{1.14-2.0log(ε/d)}²　　・・・(5)

各種工業で実用的に使用されている管に対して、相対粗さε/d、レイノルズ数Re、管摩擦係数λの関係を近似的に示す式として、次のコールブルックの式があります。

　1/√λ=-2log((ε/d)/3.71+2.51/(Re√λ))　　・・・(6)

ある程度レイノルズ数の大きい領域で実用的には、管の材質や製法から決まる平均粗さと直径から相対粗さを求めて、(6)式を対数グラフに整理したムーデイ線図とよばれる図などを基にλを一定値として読み取り、(2)式により直管損失ヘッドを求めます。

ただし、経年的に管内壁が錆や腐食で荒れてくると、相対粗さが大きくなって管摩擦係数λも増大するので、ムーデイ線図から読み取った値に対して余裕を見込んだ値を用いて損失計算します。
λが一定の場合、直管の損失ヘッドは(2)式より、長さ直径比と流速の二乗に比例します。
 

３．管路断面が非円形の場合

各種の産業や建築設備に用いられる管路には、矩形など断面が非円形の形状のものもあります。
この場合は、次式で定義される水力直径d_hを用いて、(1)のレイノルズ数、(2)のダルシー・ワイスバッハの式による直管摩擦損失や相対粗さの計算を行います。

　dh=4A/S　　・・・(7)

Aは管路の断面積、Sはぬれ縁長さと呼び、管路断面の周囲長さのことです。
（円形断面であればd_h=4xπd²/4/(πd)=dとなります。）
またA/Sを水力平均深さといいます。
 

４．各種管路要素の損失

実際の配管系統には、直管以外の様々な管路要素（曲がり、拡大、縮小、バルブなど）が存在し、これら管路要素において断面形状や方向の変化に起因する圧力損失が発生します。
管路要素における損失ヘッドをhsとすると

　hs=ζv²/2g　　・・・(8)
ζ（ゼータ）：損失係数…管路要素の種類と形状で決まります。
v(m/s)：管路要素における流速。拡大や縮小など流速が変化する場合は、速い側の流速をとります。

(8)式から管路要素における損失ヘッドは、直管と同様に流速の二乗に比例することがわかります。
ζについては各要素の形状ごとに資料から求めます。
ここではその一部を紹介します。
 

（1）管路の急収縮

図2のように、管路断面積が急激に狭まるとき、流れの慣性のために急縮小コーナ部の直後で、流れは管路面積より細くなります。これを「縮流」といいます。
その後流れは、管路一杯に広がって流れるようになりますが、このときに流れの拡大に伴う渦の発生により損失が生じます。

細い管路一杯に広がって流れるときの流速をV2、細い管路断面積をA2,縮流部の流路断面積をAcとすれば、
　損失係数　ζ=(A2/Ac-1)²=(1/Cc-1)² 　　・・・(9)
　損失ヘッド hs=ζV2²/2g=(1/Cc-1)²V2²/2g　　・・・(10)
となります。

(9)(10)式の”Cc”は収縮係数とよばれ、太い管路断面積をA1としたとき、断面積比A2/A1に対するCc、ζの値は、下表のようになります。

【表：急収縮管の損失係数（機械工学便覧より）】

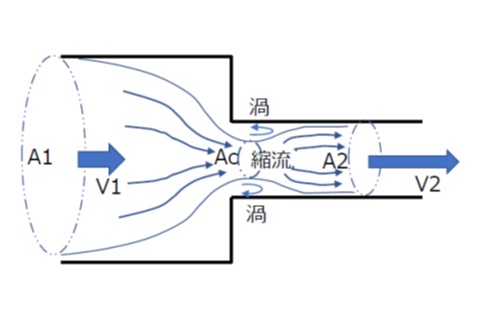
【図2　管路の急収縮】

（2）タンクから管路への入り口

急縮小で、太いほうの管路断面積が非常に大きい、つまりA1=∞、A2/A1=0の場合に相当しますが、入口部の形状により損失係数が異なります
図3のように、入り口部に丸みをつけることにより、角部のままの状態に比べて損失係数を0.1～0.01倍程度に小さくすることができます。

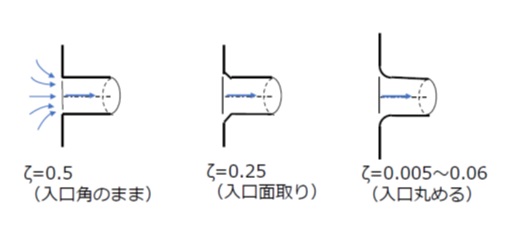
【図3　タンクから管路への入り口形状と損失係数ζ】

（3）管路の急拡大

図4のように管路断面積が急拡大する箇所では、流れがはく離することで発生する渦による損失が生じます。
細い管の断面積をA1,拡大管の断面積をA2とすれば、急拡大の損失係数は次式で計算されます。

　ζ=ξ(1-A1/A2)² 　　・・・(11)

速い側（細い管）の流速をV1とすれば、急拡大による損失ヘッドは
　hs=ζv² /2g=ξ(1-A1/A2)² x V1² /2g 　　・・・(12)

ξ（グザイ）は補正係数で、0.93～1.08の値となります。

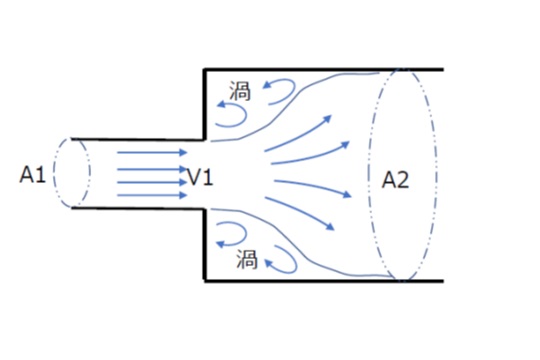
【図4　管路の急拡大】

（4）管路から貯水池やタンクへの流出

図5のような場合は、(3)の管路急拡大で、拡大管の断面積が極めて大きい、すなわち(11)式でA2=∞とみなします。
補正係数ξ=1.0 として ζ=1.0 となります。

　hs=ζv²/2g=v²/2g

つまり、管路内の速度水頭＝流出における損失ヘッドとなります。

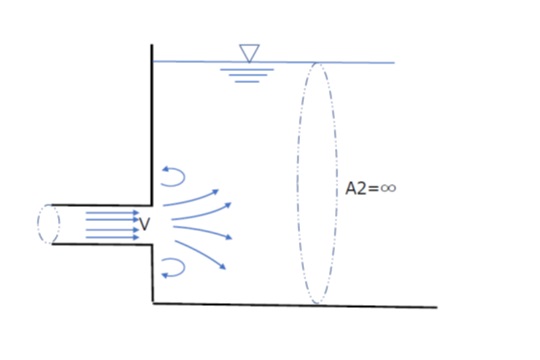
【図5　タンク、貯水池への流出】

（5）曲がり部

図6のようにある曲率半径Rをもって曲がる管路要素を「ベンド」と呼びます。
ベンドにおける損失係数については、実験結果に基づいた(13)式のようなワイスバッハの近似式と呼ばれる式があります。

　ζ=(0.131+0.1632(d/R)^3.5)(θ/90) 　　・・・(13)

管径dに対する曲がり半径Rを大きくするほど、曲がり角度θを小さくするほど、損失は小さくなります。(13)式の適用範囲は d/R=0.4～2.0 です。

なお、市販の配管継手には形状はベンドであっても「エルボ」と呼ぶものが多くあります。
このような市販品エルボにはRの大きいロングエルボとRの小さいショートエルボがあり、曲がり角についてはθ=90°のものや45°のものがあります。
ロングエルボの方が損失は少なくなりますが、配管スペースによっては取り付けられないこともあります。また、ロングエルボはショートエルボより重量が大きく価格は高くなります。
予算や配管計画に支障のない範囲で、損失の少ないロングエルボを使うようにします。

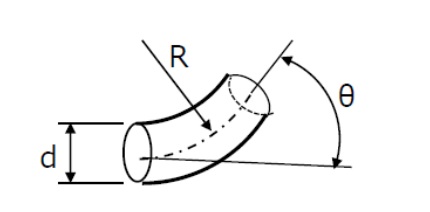
【図6　ベンド管（エルボ）】

（6）バルブ

一例として、口径25mmの仕切弁と玉型弁の全開時における損失係数を比較すると、仕切弁0.233、玉型弁6.09と非常に大きな違いがあります。
玉型弁は、全閉時の漏れをゼロにすることができて、流量の微調整も可能である等の利点がありますが、多用し過ぎると損失が大きくなります。
例えば、ある流体機器に出入りする配管の入り口側を仕切弁、出口側を玉型弁とするなど、機能と損失の両方を考えた選択を行うようにします。
 

直管損失h_Lと管路要素の損失hsを合計することにより、ある流量の流体を配管で移送する際に必要となる流体機械の性能仕様（ポンプであれば全揚程）を計算することができます。
連続の式より、流量が一定ならば配管径を大きくするほど流速が小さくなるので圧力損失を小さく、すなわち必要な流体機械の性能仕様を低減することができます。
しかし、配管径を上げることで流体機械やバルブなどの口径も大きくなりコストアップにつながることもあります。

性能仕様低減効果（ランニングコストダウン）と口径アップによるイニシャルコストアップ影響の両面から検討を行い、最適な管径を選択するようにしましょう。

 
次回の連載コラムでは、運動量の法則とその適用例について解説します。
 
（日本アイアール株式会社　特許調査部　S・Y)
 

＜参考文献＞

• 　西海孝夫 著『図解　はじめて学ぶ　流体の力学』 日刊工業新聞社、2010

※本コラムで基礎を概説した流体力学についてさらに深く学びたい方に、おススメの書籍です。

Tweet

Pocket