【機械設計マスターへの道】圧力の必須前提知識まとめ［流体力学の基礎知識②］

Tweet

Pocket

今回は、流体の挙動を調べたり利用したりする上で不可欠な物理量の一つである圧力について解説します。
 

１．圧力とは

圧力は、流体中の壁面あるいは仮想面の単位面積あたりに働く力の法線方向成分と定義されます。
静止流体中に置かれた仮想面や壁面を押す力を「全圧力」といいます。
全圧力の単位面積当たりの量が圧力となります。

全圧力をF、面積をAとすれば、圧力p=F/A　となります。

２．圧力の単位

圧力の単位は、強度設計に用いる応力と同じPa（N/mm²）です。
実用的な圧力の単位としてはkPaまたはMPaが良く用いられます。
工学単位では、kgf/cm²が使われていました。
（※工学単位については、前回の連載コラム「流体力学の基礎知識① 流体の性質」をご参照ください。）

SI単位換算と圧力の大きさのイメージは下記のようになります。

0.1MPa≒1 kgf/cm²≒1気圧

工学単位でいうところの1気圧を約10倍するとMPaになります。
1気圧（標準大気圧）は正確には0.1013MPa(1013hPa)になります。
なおバール(bar)という単位は、SI単位との併用が認められており 1bar=0.1MPa となります。
また、米国などでは慣用単位ヤードポンド系が使われており、圧力はpsiという単位で表示されます。
（psi：pound-force per square inch）

1psi≒6.89kPa

上記の換算比率を覚えておくと便利でしょう。

３．パスカルの原理

密閉容器内の静止流体の一部分に与えられた圧力は、損失なく全部分に伝達される、という特長があります。
これを「パスカルの原理」といいます。

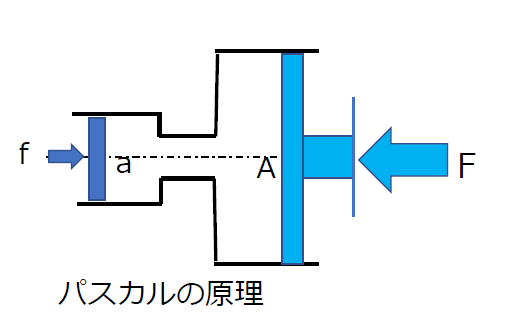
図のような連結シリンダ・ピストンにおいて、左側の小さい面積aのピストンに力fを加えると、シリンダ内には圧力p=f/aが発生します。
この圧力pは連結管を経て右側の大きい面積Aのピストンに同じ大きさで伝達し、壁面からの反力F=Ap=(A/a)fを生み出します。連結管を通じてピストンの面積比に応じた力の増幅が可能になります。

油圧ジャッキや流体ブレーキは、パスカルの原理を利用したものです。

４．絶対圧とゲージ圧

圧力を表すのに基準圧力の取り方によって、完全真空を基準とする絶対圧pAと、大気圧p0を基準とするゲージ圧pGの二通りの方法があります。

pA= p0+pG

この関係は図のように示すことができます。
 

 
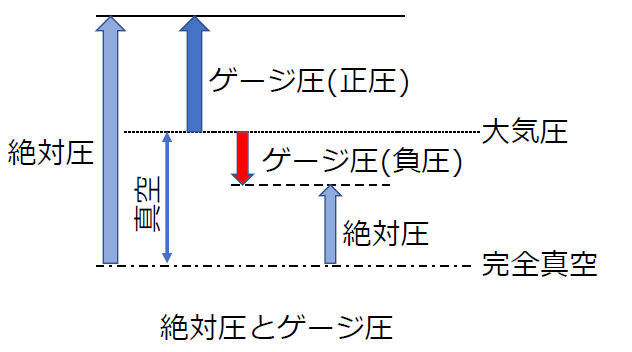
流体の圧力は、マノメータ、圧力計、圧力変換器などで測定しますが、主にゲージ圧で表示します。
大気圧より低い圧力状態を真空、真空状態における負のゲージ圧を負圧、正のゲージ圧を正圧、と呼びます。
正圧、負圧の両方を測定表示できる圧力計を「連成計」といい、通常は正圧が黒、負圧が赤で目盛表示されています。

５．密度と圧力

容器または管に密度ρの液体が入っていて液面から底面までの高さがh(m)であるとすると、底面における圧力（ゲージ圧）pとρ、ｈの間には次式の関係があります。

p=ρgh　　g:重力加速度

この液柱高さhを「ヘッド」とよびます。
ヘッドは長さ(m)の単位を持ち、液柱の高さ、あるいは液面深さの意味を持つと共に、圧力の尺度でもあります。密度が小さい液の場合は、ヘッドが大きくても（液柱が高くても）底面における圧力は小さいということが起こりえます。

液柱の高さ（差）から圧力（差）を測定する計測器が「マノメータ」です。

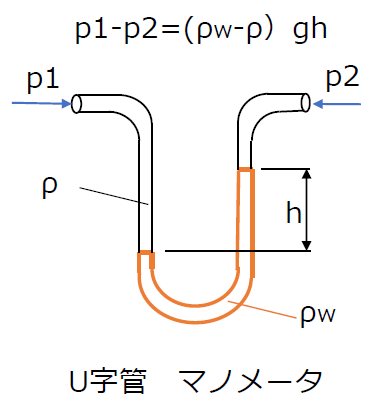
またヘッドは流れのエネルギを論じる際の尺度としても利用されます。

以上今回は、圧力について解説しました。流体を扱う上で、圧力について正しく理解することが必要です。

次回の連載コラムでは、複雑な流体の動きを考える際に重要となる「連続の式」と「ベルヌーイの定理」について解説します。
 
（日本アイアール株式会社　特許調査部　S・Y)
 

＜参考文献＞

• 　西海孝夫 著『図解　はじめて学ぶ　流体の力学』 日刊工業新聞社、2010

※本コラムで基礎を概説した流体力学についてさらに深く学びたい方に、おススメの書籍です。

Tweet

Pocket