【機械設計マスターへの道】連続の式とベルヌーイの定理［流体力学の基礎知識③］
今回のコラムでは、三次元空間を自由に流れて、その状態が場所や時間とともに変化する複雑な流体の運動を簡素化することで、工学的な問題の解決に実用的に適用することができる手法について解説します。
１．流れの状態
三次元性があって、しかも時間とともに変化する流れを関数で表すためには、位置x,y,zと時間tの4変数が必要で、速度もX,Y,Zの3方向成分で考える必要があります。
コンピュータの演算能力が向上したとはいえ非常に複雑な数値計算となって膨大な時間がかかり現実的ではありません。
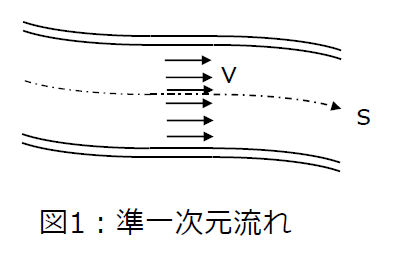
管内の流れなど多くの場合は、図１のように軸方向sにそって、管路断面積や流れの方向が緩やかに変化するとみなすことができます。
この場合は、軸方向に垂直な流れを無視して、軸方向sに沿う平均流速vで代表し、位置sと時間tの関数として簡素化して表すことができます。
v=f(s,t) ・・・（1）
上式で表される流れを「準一次元流れ」といいます。
理論上の扱いが簡単で、実用的な設計計算に広く用いられます。準一次元流れにおいては、断面平均流速vのみならず、圧力pや密度ρについても断面にわたる平均値として扱います。
流れを時間的に分類したとき、時間とともに状態が変化する流れを「非定常流」、変化しない流れを「定常流」といいます。定常流の場合、平均流速は次式で表され、位置のみの関数となります。
v=f(s) ・・・（2）
２．連続の式
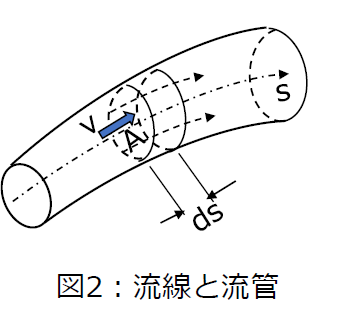
準一次元流れに沿った1つの仮想線を考え、その両側の流体が線を境として互いに入り混じることがないような線を「流線」といい、流線で囲まれる任意断面を持つ仮想の管を「流管」といいます。図2に概念を示します。
流管に対して質量保存則を適用します。
質量保存則とは物質の体積が変化しても系全体の質量の総和は一定となる法則のことです。
流管内の中心にある流線に沿って座標sを設け、微小長さdsの微小要素を考えます。
流管の断面積をA、平均流速をv、平均密度をρとします。
位置sと時間tは互いに独立な変数であることから流管における質量保存則は次の式で表すことができます。
∂/∂t(ρA)+ ∂/∂s(ρAv)=0 ・・・（3）
この式を一次元の連続の方程式といいます。
定常流と連続の式
定常流の場合、時間tとともに流れが変化しないことから（3）式は左辺第2項のみとなり、位置sで積分すれば次式の関係が得られます。
Qm=ρAv=const. ・・・（4）
Qmは、流管微小要素断面を通過する単位時間当たりの質量を表し「質量流量」と呼ばれます。
SI単位はkg/sとなります。
水や油など非圧縮性流体の場合はρ=const.であり（4）式は
Q=Av=const. ・・・（5）
となります。
（4）,（5）式を定常流に適用される連続の式といいます。
（5）式のQを流量（または体積流量）といい、SI単位はm3/sとなります。
ただし、実用面ではm3/minなど様々な単位が使われます。
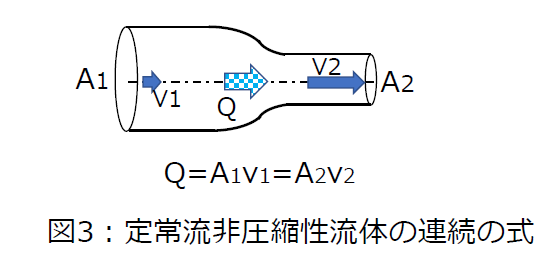
非圧縮性流体の定常流で図３のように、断面積A1が大きければ流速v1は遅く、断面積A2が小さければ流速v2は速くなり、
Q=A1v1=A2v2 ・・・（6）
の関係が成り立ちます。
連続の式は粘性のある流体にも適用することができ、管路や流体機器内の多くの流れに実用的に利用されます。
３．ベルヌーイの定理
ある流管内を流れる流体が保有する機械的エネルギーには、運動エネルギー、位置エネルギーおよび圧力エネルギーがあります。
位置に関して基準水平面からの高さをz、圧力をpとすれば、非圧縮性であって、粘性による摩擦損失などのエネルギー損失がない「理想流体」の場合、エネルギー保存の法則から次式の関係が成り立ちます。
1/2v2+p/ρ+gz=const. ・・・（7）
（7）式の各項は単位質量当たりの流体の持つエネルギーを表し、これは理想流体の定常流において、流管に沿う任意の点におけるエネルギーの総和は一定に保たれることを示すものです。
（7）式の両辺にρをかければ、
1/2ρv2+p+ρgz=const. ・・・（8）
と書き換えることができます。
これが「ベルヌーイの定理」（または「ベルヌーイの式」）と呼ばれるものです。
動圧、静圧、全圧
上記（8）式の左辺第1項は、単位体積当たりの流体が持つ運動エネルギーで「動圧」と、第2項は圧力エネルギーで「静圧」と呼びます。
また、第3項は、単位体積当たりの流体の持つ位置エネルギーを表します。
第3項の位置エネルギー変化が無視できる場合は、
1/2ρv2+p=const. ・・・（9）
となります。
すなわち動圧と静圧の和は一定となることを示し、動圧と静圧の和を「全圧」といいます。
また（9）式は、流れの速度が上がると圧力は低下し、速度が下がると圧力は上昇する、という流れの基本的な性質を表しています。
駅のプラットフォームで通過する電車の近くに立つと、電車の通過に伴って発生する気流の速度ｖのために気圧ｐが低下し、V=0で元の気圧状態にあるプラットフォーム中側から電車側へと圧力差で押し出され（感覚としては吸い寄せられ）ようとします。時速50km/hで、大人の体面積を0.8m2程度として試算すると10kg近い力を受けることになります。通過する電車からは十分に離れて待たなければ危険です。
流れの速度を減じることで圧力を上げる、ということは渦巻きポンプなどのターボ形流体機械を設計するうえで基本的に必要な原理です。
さらに（7）式を重力加速度gで割って書き換えれば、
v2/2g +p/ρg +z=H ・・・（10）
と表すことができます。
左辺第1項を「速度ヘッド」、第2項を「圧力ヘッド」、第3項を「位置ヘッド」、これらの総和を「全ヘッド」といいます。ヘッドは長さの単位(m)を持ちます。
摩擦損失を考慮したベルヌーイの式
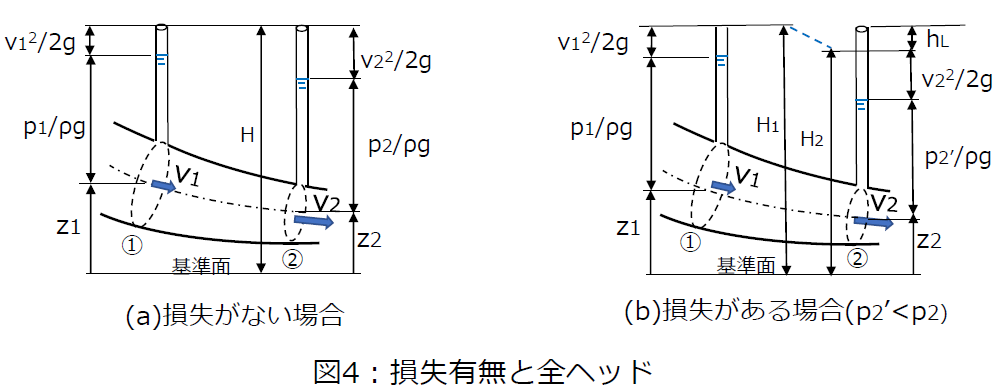
上記（10）式の関係を、図4(a)のように管路にマノメータを取付けたときの様子で理解することができます。
実際の流れにおいては、流体の有するエネルギーは、粘性による摩擦などのために一部が熱エネルギーに変換されるので、外部からのエネルギー補給がない限りは図4(b)のように流れに沿って全ヘッドは減少していきます。
断面①から②におけるエネルギー損失をhLとすれば、次のようになります。
v12/2g+p1/ρg+z1= v22/2g+p2/ρg+z2+hL ・・・（11）
(11)式は、粘性による摩擦損失を考慮したベルヌーイの式であり、管内の流れ損失などを見積る場合の実用的な式として利用されます。
流速vは管路断面積で決定され、位置エネルギーｚは管路配置で決定されますので、エネルギー損失の分だけ、圧力pが減少することになります。このため管路におけるエネルギー損失を圧力損失（圧損）ともいいます。
圧縮性を考慮したベルヌーイの式
気体など圧縮性のある流体では、密度ρの変化を考慮する必要があります。
また気体の場合、運動エネルギー、圧力エネルギー、位置エネルギーに、内部エネルギーを加えた、熱力学的な扱いが必要となります。
詳細な導出過程については省略しますが、理想気体であって断熱変化をするという条件において、気体に関するベルヌーイの定理は、次の式のようになります。
1/2v2+｛κ/(κ-1)｝p/ρ+gz=const. ・・・（12）
（κ：比熱比）
上記（12）式左辺第2項は、単位質量当たりの内部エネルギーと圧力エネルギーの和、つまり比エンタルピーを表します。
《参考ページ：熱力学の基礎知識・用語の解説》
内部エネルギー、比熱比、比エンタルピー等の熱力学用語については、以下のコラムをご参照ください。
- 熱力学の基礎知識①「熱と仕事とエネルギー」
- 熱力学の基礎知識②「第一法則と第二法則」
- 熱力学の基礎知識③「気体の状態変化」
ベルヌーイの定理は、理想流体・準一次元流れ・定常流を前提としていますが、（11）式のように摩擦損失を考慮すれば粘性のある流体にも適用することが可能で、流体を扱う様々な場面で実用的に利用されます。
特に流量測定・流速測定にはベルヌーイの定理を応用したものが多くあります。
［※関連コラム：ベルヌーイの定理と流量・流速の測定はこちら］
次回の連載コラムでは、流体力学シリーズの続きとして管路における圧力損失について解説します。
（日本アイアール株式会社 特許調査部 S・Y)
＜参考文献＞
- 西海孝夫 著『図解 はじめて学ぶ 流体の力学』 日刊工業新聞社、2010
※本コラムで基礎を概説した流体力学についてさらに深く学びたい方に、おススメの書籍です。
- 社会人のための流体力学 ［※社会人のための機械工学シリーズ 第3回］（講師：技術士 近藤孝邦 氏）
