【機械設計マスターへの道】気体の状態変化［熱力学の基礎知識③］

Tweet

Pocket

熱力学の原理を利用する機械では、作動物質として気体を扱うものが数多くあります。
気体の状態変化について理解することは、熱力学を学ぶ上で非常に重要です。

１．理想気体

気体の状態変化を論ずる上では先ず、気体分子間の相互作用のない仮想的な状態である理想気体に関する法則が基礎となります。
理想気体は、気体の温度T、圧力p、体積Vの間に、ボイル・シャルルの法則が成立するものを指します。
気体分子間の相互作用がない仮想的な状態です。
実在気体でも、常温常圧における空気や、低圧高温における蒸気など、気体の種類と一定の条件においては理想気体の法則を適用することができます。

＜ボイル・シャルルの法則＞

一定量の気体の体積は、圧力に反比例し、熱力学的温度に比例して変化する.
これを式で表せば、

pV/T=Const.　・・・（1）

となります。
 

２．状態方程式

(1)式において、気体１mol当たりのモル*）体積Vmを用い、定数Rを用いて表すと

pVm=RT　・・・（2）

と書くことができます。

気体の物質量がn [mol]であれば、（2）式は

pV=nRT　・・・（3）

となります。

ここに　Rは、気体定数（モル気体定数あるいは一般気体定数とよぶ場合もあります）といい、気体の種類によらない一定値　8.314 [J/(mol・K)]　をとります。
（2）、（3）式を理想気体の状態方程式といいます。

比体積ｖ［ｍ^３/kg］を用いて表すと状態方程式は次のようになります。
モル質量を　M[kg/mol]とすれば

pv=（R/M）T＝RmT　・・・（4）

ここにRm［J/(kg・K)］を気体定数とよぶことがありますが、Rmはモル質量に依存するので、気体の種類によって異なる数値となります。Rmの値は軽い気体ほど大きく、重い気体ほど小さくなります。
軽い気体の例として水素H₂はモル分子量2.016×10^-3、Rm=4124[J/kg・K]。
重い気体の例として二酸化炭素CO₂はモル分子量44.01×10^-3、Rm= 188.9[J/kg・K]。

気体定数には 気体の種類によらず一定のものと、気体によって値が異なるものがあり、それぞれ単位が異なるのでその意味と使い分けに注意しましょう。

*）アボガドロ数　6.02 x10²³ 個の粒子（原子や分子）を含む系の物質量を1 molといい、標準状態（0℃、大気圧）では気体の種類によらず1molは22.4リットルになります。
 

３．熱容量と比熱

物質の温度を1°K 上昇させるのに必要な熱量を「熱容量」、単位質量（1[kg]）当たりの熱容量を「比熱」（比熱容量）、1molあたりの熱容量を「モル熱容量」といいます。
熱容量をC[J/K]、比熱（比熱容量）をc[J/(kg・K)]、モル熱容量をC_m [J/(mol・K)]、質量m [kg]、物質量n [mol]　とすれば、物質の温度を⊿T[°K]変化させるのに必要な熱量Qは、

Q=C⊿T=mc⊿T＝n C_m⊿T　[ J ]

気体の場合、温度を上げるのに必要な熱量は、一定圧力のもとで加熱する場合と、一定容量のもとで加熱する場合で異なります。
圧力一定とするときの比熱を「定圧比熱」、体積一定とするときの比熱を「定容比熱」といいます。
比熱ｃとモル熱容量C_mを、それぞれ定圧と定容で区別して、ｃ_ｐ、C_mｐを定圧比熱容量、ｃ_ｖ、C_mｖを定容比熱容量、といいます。
等圧のもとで気体が熱を受けると、膨張により外界へ仕事を行うのでその分だけ、定圧比熱は定容比熱よりも大きくなります。

定圧比熱容量と定容比熱容量の比を、比熱容量比κといいます。

κ=ｃ_ｐ /ｃ_ｖ = C_mｐ / C_mｖ　・・・（5）

理想気体の場合、モル熱容量と気体定数Rの間には、次の関係があります。

C_mｐ – C_mｖ =R （ｃ_ｐ-ｃ_ｖ=Rm）　・・・（6）

これをマイヤーの関係といいます。

また、（5）（6）式から、次式の関係が得られます。

C_mｐ=κ/(κ-1) R, C_mｖ=１/(κ-1) R　・・・（7）

４．ｐ-V 線図と仕事

状態方程式は圧力p、体積V、温度Tという3つの状態量の関係を規定するものですが、3つの状態量のうち、2つを定めれば残りの一つも定まり、気体の状態が決定されます。
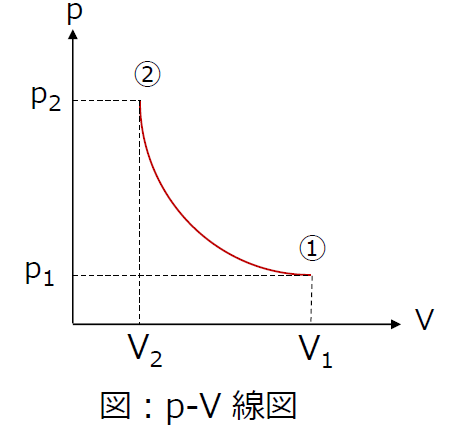
2つの状態量として縦軸に圧力、横軸に体積（1molまたは1kg当たり）をとったp-V 線図が良く用いられます。
図の①(p1,V1)→②(p2,V2)の状態変化は圧縮、②→①は膨張、となります。
気体が外部に対して仕事をしたり、外部から仕事を受けたりするとき、仕事量はp-V 線図上の面積として表されます。

密閉されたシリンダ内の気体が、流れを伴わずにピストンから仕事を受けてわずかに圧縮されたとします。
体積変化をdV,ピストンに加わる圧力をpとすれば、微小仕事dWは、dW＝pdV
① →②の状態変化をするときの全仕事は、微小仕事を積分して

W=∫₁² p dV　・・・（8）

仕事 W は、図の①，②、V₂、V₁　で囲まれる面積になります。

 

５．絶対仕事と工業仕事

式（8）のように、流れを伴わない系に外部から与えられる仕事を「絶対仕事」といいます。
実際の熱機関では、動作流体を吸気して仕事をした後に排気するサイクルを構成するので流れを伴う開いた系となります。この時の仕事を、工業仕事Wｔといいます。
流れを伴う系では、気体が系に出入りするための仕事dpVが必要となり、工業仕事の微小成分は、dWt=-Vdp で表されます。

図で、流れを伴うときの①→②の圧縮仕事は次式で表されます。
Wt=-∫₁² V dp　・・・（9）(-は外界に対して仕事をすることを意味する)
工業仕事 Wtは、図の①，②、p2、p1　で囲まれる面積になります。

 
次回は、熱力学におけるサイクル（カルノーサイクル・逆カルノーサイクル）についてご説明します。

 
（日本アイアール株式会社　特許調査部　S・Y)

Tweet

Pocket