【機械設計マスターへの道】第一法則と第二法則［熱力学の基礎知識②］
今回のコラムでは、熱力学の法則について解説します。
１．熱力学の第1法則
機械的仕事は熱に変換されます。
エネルギーが変換されるとき、これによってエネルギーが消滅したり、新しく作られたりすることはなく、同じ能力は保存されます。別の言い方をすれば、1つの系において、外部との間にエネルギの出入りがない限り、エネルギの総和は一定である、ということができます。これをエネルギー保存の法則といいます。
熱力学の第1法則は、熱も仕事もエネルギーの一形態であって、両者間にエネルギー保存の法則が成り立つことを示しています。すなわち、熱と仕事は同じエネルギーの一つの形であり、仕事を熱に変えることもその逆も可能である、ということができます。
２．内部エネルギーとエンタルピー
外界から系に熱が加わると、系内の分子の運動が活発になり、系内に蓄えられるエネルギーが増大し、気体の温度が上昇します。このように分子の運動エネルギーの増加に使われる熱量を「顕熱」といいます。
一方、熱を加えても温度が変化せず、分子間力すなわち分子の集合状態を変化させるために使われる熱量を「潜熱」といいます。液体から気体の状態に変化するために潜熱を必要とします。このため、周囲の空気から熱を奪うため、気温が低下します。（打ち水の効果、あるいはクーラの原理）
系内に蓄えられる顕熱や潜熱は系内分子のエネルギーの総和であり、これを内部エネルギーUといいます。一般にUの絶対値を求めることは不可能であり、状態変化時のエネルギ変化量⊿Uで扱います。
気体にQ［J］の熱量が加えられ、内部エネルギーが⊿U[J]増加し、外界に対してW[J]の仕事をしたとします。
このとき、Q=⊿U+W［J］ の関係が成立します。これが熱力学の第1法則を表す式です。
定圧変化（P=一定）の場合体積変化を⊿Vとすれば、機械的仕事WはW=P⊿Vとなります。
（※詳しくは、連載コラム「熱力学の基礎知識① 熱と仕事とエネルギー」のページをご参照）
したがって、
Q=⊿U+P⊿V=⊿(U+PV)
内部エネルギーと仕事の和U+PVをまとめて一つの量として扱うと、熱力学の諸現象を扱う上で便利になることが多くあります。
この量に記号Hを用いて
H=U+PV [J]
Q=⊿H=⊿U+P⊿V
Hはエンタルピーとよばれる状態量であり、U,P,Vの関数となります。
単位重量当たりのエンタルピーを比エンタルピーh［J/kg］といいます。
３．熱力学の第2法則
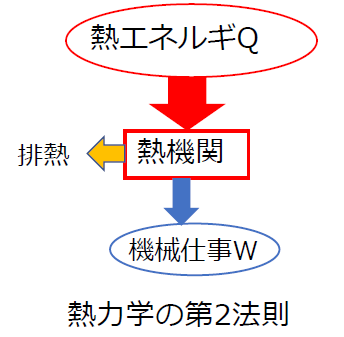
熱機関では、熱エネルギーをすべて仕事に変換することはできません。
一方、機械が仕事をすると、軸受で摩擦熱が発生して軸受温度が上昇するなど、仕事は容易に熱に変換されます。
しかし摩擦熱で軸を回転させることは不可能です。
熱を仕事に変えることは、仕事から熱への変換より難しく、熱力学の第1法則だけでは説明することができません。
熱と仕事の不可逆的な関係を説明するのに、熱力学の第2法則が必要となります。
この法則は先人により次のように述べられています。
- クラジウス： 熱はそれ自体では、低温物体から高温物体へ移動することはできない
- ケルビン（トムソン）： 熱機関が仕事をするためには、常に熱源より温度の低い物体を必要とする。すなわち、高熱源から熱を吸収して、その一部を仕事に変え、残りは低熱源に捨てなければならない
熱力学の第2法則は、熱移動の方向性、熱を仕事に変換するとき高温物体と低温物体の間で熱移動させる必要があることを述べたものです。
４．エントロピー
エントロピーSとは次の式で定義される状態量です。
⊿S=⊿Q/T （Q：熱量、T：温度）
系の状態１と２におけるエントロピーをそれぞれS1、S2とすると
可逆変化に対してはS2-S1=0
不可逆変化に対してはS2-S1>0
エントロピーは増大することはあっても減少することはなく、自然界の熱の流れは、エントロピーの総和が増大する方向に進む、ことを意味します。
これをエントロピー増大の原理といい、熱力学の第2法則の表現方法の一つです。
次回の連載では、気体の状態変化（理想気体、状態方程式、熱容量と比熱など）を解説します。
（日本アイアール株式会社 特許調査部 S・Y)
- 社会人のための熱力学 ［※社会人のための機械工学シリーズ 第2回］（講師：技術士 近藤孝邦 氏）
