振れ公差は回転部品に使う幾何公差|円周振れ/全振れの違いと使い方

前回の幾何公差に関する解説記事では、位置公差の種類や特徴、使い方を説明しました。
今回は、軸などの回転部品に使う「振れ公差」について解説します。
目次
1.振れ公差とは?
「振れ公差」は、部品を回転させたときの振れ(表面の変位)を規制する幾何公差です。
そのため、軸・ローラ・コロなど、主に回転させて使う円筒部品における、表面の機能要求に活用できます。
前回ご説明した位置公差の「同軸度」も円筒部品に使いますが、同軸度の場合は円筒の軸線を評価するため、規制する対象が異なることに注意してください。
振れ公差の場合は軸線ではなく、回転する円筒部品の表面を評価するものだと覚えておきましょう。
また、振れ公差は「真円度」や「円筒度」などと同様に形状を規制する幾何公差ですが、回転の中心となる軸線にデータムを指定する必要があります。
そのため振れ公差が指示される形体は、データムを必要とする関連形体になります。
振れ公差の種類
表1のように、振れ公差には「円周振れ」と「全振れ」の2つの種類があります。
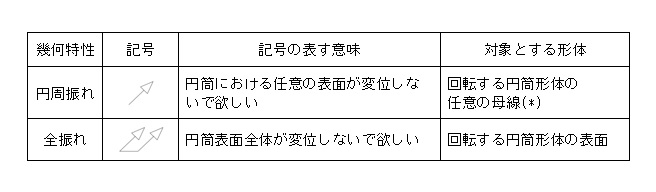
【表1 振れ公差の種類】
(*)母線とは、表面上の任意の位置における実体のある線のこと。
それでは、2つの振れ公差について解説していきます。
2.円周振れ
(1)円周振れとは
「円周振れ」は、データム軸直線を中心に回転させた円筒部品において、その任意の位置にある表面が変位しないで欲しいと、形体に対して指示する幾何公差です。
円周振れで規制できる形体は1本の母線であり、部品を回転させたときの半径方向の円筒表面または軸線方向の円筒端面における、母線の変位を規制します。そのため、図1に示すように、その1本の母線を囲む、同心の大小2円の間や、2直線の間が公差域になります。
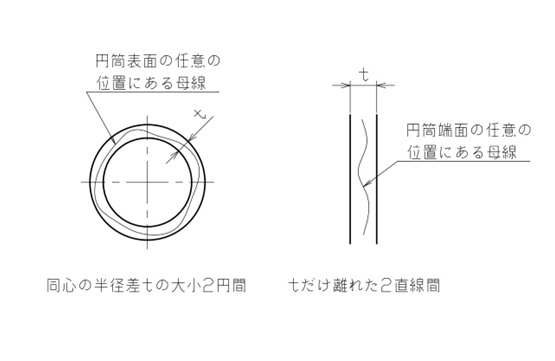
【図1 円周振れの公差域】
(2)円周振れの使い方
① 半径方向の円周振れ指示
まず、半径方向の変位を規制したいときの指示方法から解説します。
軸受で支えられる円筒部品で、左側円筒表面の任意の位置における回転振れを抑えたい場合を想定し、回転時の半径方向の変位は0.1mmまで許容できるとします。
この場合、図2のように軸受に挿入される右側円筒の軸線にデータムを指定し、データム軸直線Aとします。
規制対象は軸線ではなく、左側円筒表面の母線なので、寸法線の延長線上から外した位置に円周振れを指示してください。
なお、同心の大小2円の間が公差域になるため、公差値の前に直径記号のφは付けません。
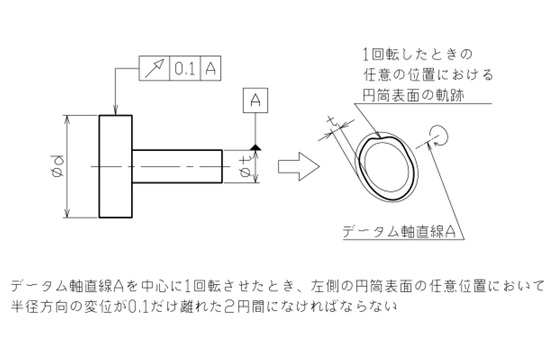
【図2 円周振れの図示例と解釈①】
また、図3のように円筒の両端を軸受で支えるような部品であれば、円筒両端の軸線へデータムを指定します。そして図2と同じように、変位を規制したい表面(真ん中の円筒)に円周振れを指示してください。
この場合、共通データム(*)軸直線A-Bを回転させたときの、半径方向の回転振れを抑える図面指示になります。
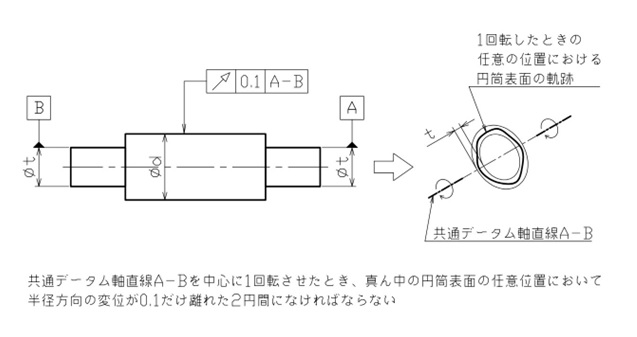
【図3 円周振れの図示例と解釈②】
(*)共通データムとは、2つのデータムによって設定される1つのデータムのことです。
図4のように、複数に分かれているデータムを、測定治具を利用することで1つのデータムとして考えることができます。
共通データムであることを示すには、図3で示したように「A-B」とハイフンを付けて表記します。
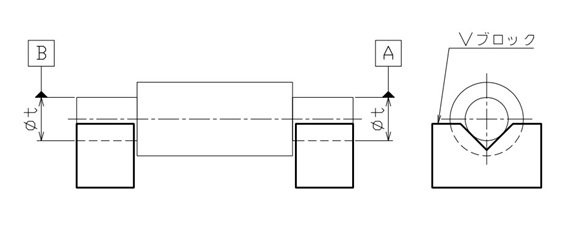
【図4 測定治具(Vブロック)を利用した共通データムの例】
② 軸線方向への円周振れ指示
次に、軸線方向の変位を規制したいケースを説明します。
軸受で支えられた円筒部品の左側端面における回転振れを抑えたい場合を想定し、軸線方向の変位は0.1mmまで許容できるとします。
この場合、図5に示すように軸受に挿入される右側円筒の軸線にデータムを指定し、変位を抑えたい左側の円筒端面へ円周振れを指示しましょう。2直線の間が公差域になるため、公差値の前にφは付きません。
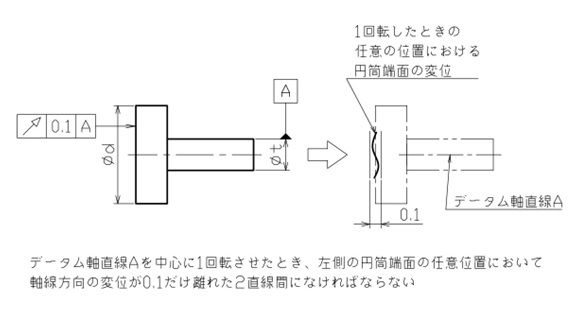
【図5 円周振れの図示例と解釈③】
3.全振れ
(1)全振れとは
「全振れ」は、円周振れのように回転部品の一部の表面だけを評価するのではなく、表面全体の変位を評価します。
円周振れの場合、テーパー型やくびれ型のような表面全体の形状のバラツキは規制できません。このような形状を望まず、表面全体を規制したいのであれば全振れを使うとよいでしょう。
全振れも、円筒部品を回転させたときの半径方向や軸線方向の変位を規制します。したがって、図6のようにその回転表面を囲む2円筒や2平面の間が公差域になります。
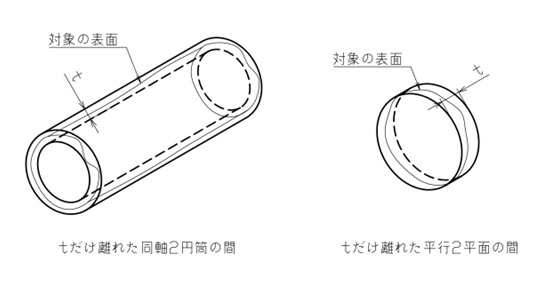
【図6 全振れの公差域】
(2)全振れの使い方
① 半径方向への全振れ指示
まず、半径方向の変位を規制したいときの指示方法から解説します。
両端を軸受で支えられた円筒部品において、真ん中の表面全体の回転振れを抑えたい場合を想定し、回転時の半径方向の変位は0.1mmまで許容できるとします。
この場合、図7のように、まず軸受に挿入される円筒の軸線にデータムをそれぞれ指定します。そして、変位を規制したい真ん中の円筒表面に対し、寸法線の延長線上から外した位置に全振れを指示するとよいでしょう。
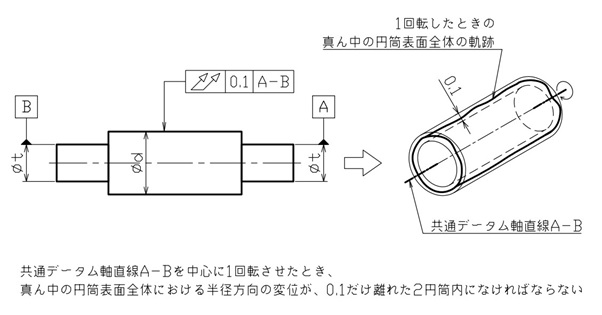
【図7 全振れの図示例と解釈①】
全振れの基本的な指示方法は円周振れと同様です。図3と図7を比較するとわかるように、円周振れと全振れの指示方法の違いは、幾何公差の記号を変えているだけです。
② 離れた位置にある円筒面への全振れ指示
規制したい表面が離れている場合は、図8のように個別に全振れを指示します。
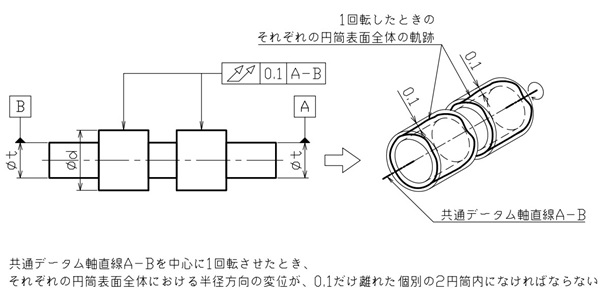
【図8 全振れの図示例と解釈②】
なお、それぞれの表面を共通の公差域で規制したいときは、形状公差の記事で解説したように、公差値の後に「CZ(共通公差域)」の記号を付けるとよいでしょう(図9参照)。
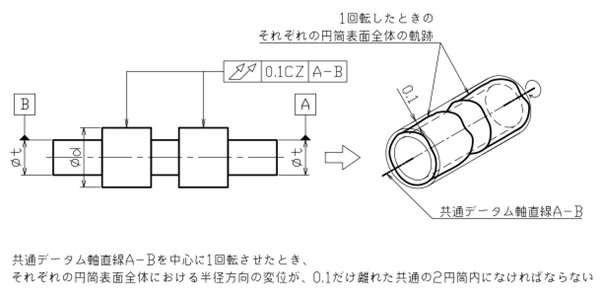
【図9 全振れの図示例と解釈③】
③ 軸線方向への全振れ指示
次に、軸線方向の変位を規制したいケースを説明します。
円筒端面全体の変位を規制したい場合も、記号が異なるのみで、その他の指示方法は円周振れと同様です。
図10のように、軸受に挿入される右側円筒の軸線にデータムを指定し、回転振れを抑えたい左側の円筒端面に全振れを指示するとよいでしょう。
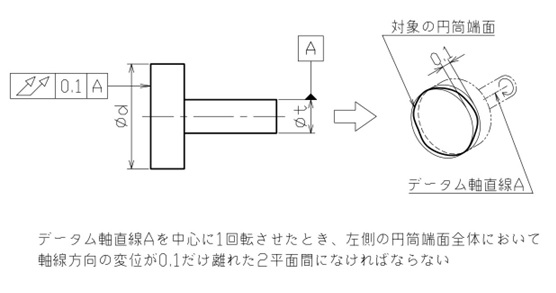
【図10 全振れの図示例と解釈④】
《軸線方向への全振れ指示と直角度の違い》
軸線方向への全振れ指示は、姿勢公差の「直角度」と似ていると思うかもしれません。実際、軸線方向に全振れを指示した場合と、直角度を指示した場合の公差域の解釈は基本的に同様です。
それぞれの使い分け方として、回転部品には全振れ、固定部品には直角度を使うのが一般的です。たとえば、全振れは歯車やカムシャフト、ボルトやナットの座面などに対して使われます。
なお円周振れの場合は、円筒端面全体ではなく任意の位置しか規制しないため、直角度における公差域の解釈とは異なることに注意してください。
(アイアール技術者教育研究所 Y・D)
《参考文献・サイト》
- 「図面って、どない描くねん! LEVEL2(第2版)」(2017)日刊工業新聞社
- 「実用設計製図 幾何公差の使い方・表し方(第2版)」(2019)日刊工業新聞社
- 「幾何公差ハンドブック」(2012)日経BP
【連載】幾何公差を学ぶコラムシリーズ(全6回)
- ゼロから学ぶ 幾何公差図面の読み方[藤崎 淳子 講師]
- 幾何公差の基礎と実践活用《演習付き・1日徹底習得》[小畠 祥平 講師]