形状公差は部品の形そのものを規制する幾何公差|真直度/平面度/真円度/円筒度の使い方

前回は幾何公差の意味や種類、サイズ公差との違いなどについて説明しました。
今回は、幾何公差の一種である「形状公差」を解説します。
部品の機能を左右する、重要かつ基本的な特性ですので、ぜひ学んでみてください。
目次
1.形状公差(形状偏差)とは
「形状公差」は、指示した平面や直線などの形体(*)が、理想の形状からどこまで偏っていいかを規制します。
この公差は、対象部品のどこかを基準に形体を規制するのではなく、その形だけを問題とするのが特徴です。
そのため、公差域を規制する基準になるデータムを必要としません。
(*)形体とは、幾何公差の対象になる点や線、平面などのことです。特に、形状公差が指示される形体のことを「単独形体」と呼びます。
形状公差の種類
表1のように、形状公差には4つの種類があります。

【表1 形状公差の種類】
理想的な形状からの偏りは、上記の4種類で規制できると知っておくといいでしょう。
使用頻度でいえば、①平面度、②真直度、③真円度、④円筒度の順番になります。
「輪郭度公差」も、単独形体の形を規制する場合は形状公差に含まれますが、本連載では分けて扱います。
それでは各公差について解説していきます。
2.真直度
(1)真直度とは
「真直度」は、形体に対して「真っすぐであって欲しい」と指示する幾何公差です。
真直度で規制できる形体は「直線形体」のみであり、稜線や母線、軸線などが該当します。
真直度は1本の直線を規制するので、その直線形体を覆うような、平行な2平面間や円筒状の空間が公差域になります(図1参照)。
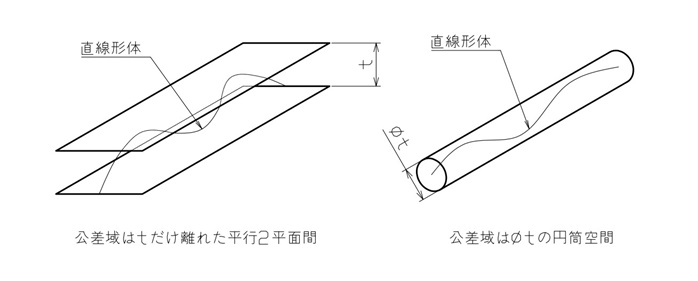
【図1 真直度の公差域】
(2)真直度の使い方
真直度は、円筒形状の部品に対して使うことが多いです。
機能上、反りやうねりが許されない軸などに指示します。
円筒軸を相手部品の穴に挿入するとし、軸の曲がりは0.1mmまで許容する場合を想定します。穴に軸を挿入する場合、軸線を基準に設計するので、真直度の規制対象は軸線にするといいでしょう。この場合、図2のように直径寸法の延長線上へ真直度を指示します。
また円筒の軸線の真直度は、方向性を問わない公差域によって規制されることが多いです。
そのため、公差値の前に直径記号のφ(ファイ)を付けて、公差域が直径0.1mmの円筒内になるよう指示してください。
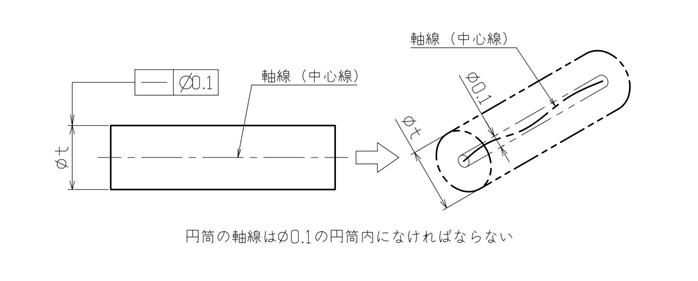
【図2 真直度の図示例と解釈】
図2では、軸線さえ真っすぐであれば良いという解釈なので、軸の形状自体は規制していません。
そのため、軸の表面がゆがんだり、テーパーのような形状になったりすることも許容されます。
3.平面度
(1)平面度とは
「平面度」は、形体に対し「真っ平らであって欲しい」と指示する幾何公差です。
平面度によって規制されるのは1枚の平面なので、平面度の公差域は、図3に示されるようにその平面形体を挟む2枚の板の間になります。
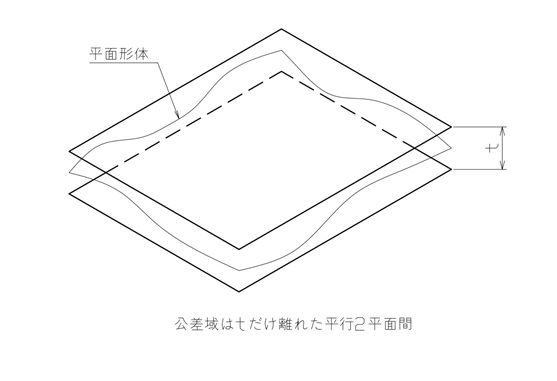
【図3 平面度の公差域】
(2)平面度の使い方
平面度は、面の精度が必要な取り付け面などに指示します。
相手部品との取り付け面において、反りの程度が0.1mmまで許容できるとすれば、図4のように指示するといいでしょう。
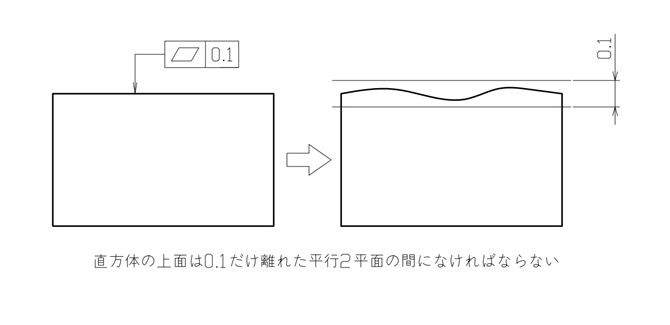
【図4 平面度の図示例と解釈】
また、離れた面に対して平面度を指示することもできます。このとき注意したいのは、いずれの面も同一の平面としたい場合です。
その場合は、図5に示したように公差値とともに「CZ(共通公差域)」の記号を付けてください。
この記号によって、離れた位置にある形体でも共通の公差域に含められます。
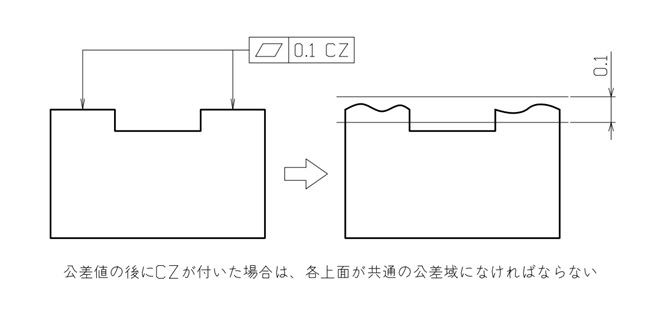
【図5 平面度の共通公差域の図示例と解釈】
(3)CZを付けるかどうかの判断
CZの要否を判断する一例として、「取り付け面に付くのが一つの部品なのか、それとも別々の部品が付くのか」どうかが挙げられます。
図6の上図は、相手部品との取り付け面が離れていて別々の部品を取り付けたいケースです。CZを付けずに指示すると、それぞれの面を個別に規制することになります。
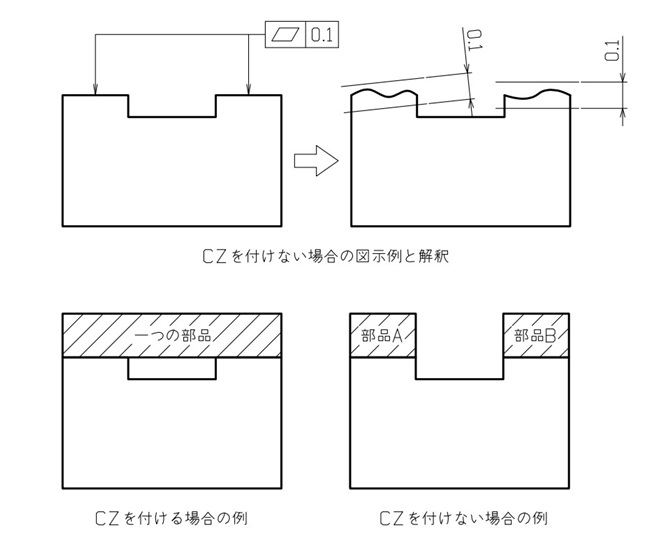
【図6 CZの要否の一例】
4.真円度
(1)真円度とは
「真円度」とは、形体に対して「真ん丸であって欲しい」と指示する幾何公差です。
図7のように、真円度の規制対象は1つの円であり、その円形体を挟む、同心の大小2円の間が公差域になります。
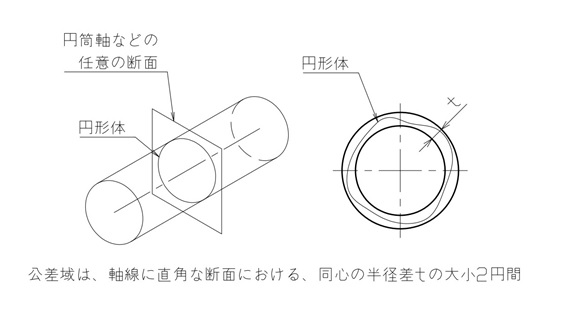
【図7 真円度の公差域】
(2)真円度の使い方
真円度は、円筒軸だけでなくテーパー形状の軸にも適用可能です。
円筒軸やテーパー軸の断面が、真ん丸な真円であって欲しく、真円からの狂いは0.1mmまで許容できる場合を想定します。この場合、図8のように指示するといいでしょう。

【図8 真円度の図示例と解釈】
各軸の任意の断面が、公差域である同心2円に入るよう規制しています。
このとき、公差値の前にφは付けないでください。真円度という名前だと公差値の前にφを付けたくなりますが、真円度は大小2円の半径差なのでφは付きません。
また、真円度の規制対象は軸線でないため、軸線を表す寸法線の延長線上からは外して指示します。
5.円筒度
(1)円筒度とは
「円筒度」とは、「形体が真っすぐかつ真ん丸であって欲しい」場合に指示する幾何公差です。
円筒度の規制対象は1つの円筒であり、その円筒形体を挟む、2円筒の間が公差域になります(図9参照)。
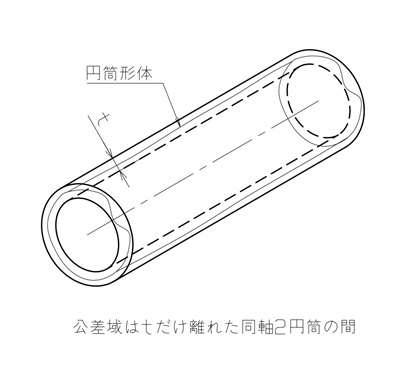
【図9 円筒度の公差域】
(2)円筒度の使い方
断面が真円で反りのない軸が必要であり、真円からの狂いと軸線方向の反りを0.1mmまで許容するとします。この場合は、図10のように指示するといいでしょう。
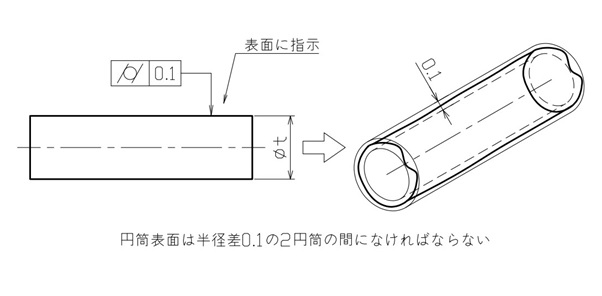
【図10 円筒度の図示例と解釈】
図10では、円筒全体の表面が、半径差0.1mmの2円筒の間にあることを規制しています。
真直度と同様に、円筒度にも直径記号φを付けたくなりますが、付けないのが正解です。また、軸線に対して指示するわけではないので、寸法線の延長線上からは外して指示します。
(3)円筒度を使う際の注意点
最後に円筒度を使う際の注意点をお伝えします。
① 円筒度はテーパー形状などには指示できない
円筒度と真円度はどちらも形体の真ん丸さを規制する公差ですが、円筒度が円筒全体を評価するのに対し、真円度は任意の断面を評価する部分が異なります。真円度は、テーパー形状のような直径の変化を伴う形体にも指示可能ですが、円筒度は指示できないことに注意してください。
② 円筒度の検査は一般に難しい
一般に円筒度公差は検査の難しい公差であり、三次元測定機が必要になります。三次元測定機を用意できない場合は、簡易的な検査にならざるをえません。そのため、設計上許されるのであれば、真直度と真円度を組み合わせて、真っすぐさと真ん丸さを規制するのがおすすめです。
以上、形状公差(形状偏差)の特徴や使い方を説明しました。
次回は、対象とする形体のある基準からの姿勢を問題にする、姿勢公差について解説します。
また、アイアール技術教育研究所では本コラム以外にも、定期的に開催されるWebセミナーやeラーニング講座で、幾何公差を学ぶことができます。この機会にご利用してみてはいかがでしょうか?
(アイアール技術者教育研究所 Y・D)
《参考文献・サイト》
- 実用設計製図 幾何公差の使い方・表し方(第2版) (2019)日刊工業新聞社
- 図面って、どない描くねん! LEVEL2(第2版)(2017)日刊工業新聞社
- 設計者は図面で語れ! ケーススタディで理解する幾何公差入門(2020)日刊工業新聞社
- 株式会社ファム 「真直度のトラブル事例②」(WEBサイト)
【連載】幾何公差を学ぶコラムシリーズ(全6回)
- ゼロから学ぶ 幾何公差図面の読み方[藤崎 淳子 講師]
- 幾何公差の基礎と実践活用《演習付き・1日徹底習得》[小畠 祥平 講師]