　　記事・コラム　　機械工学　　輪郭度公差は曲線や曲面に使う幾何公差｜線の輪郭度／面の輪郭度の使い方

2022.06.22 2024.02.26

輪郭度公差は曲線や曲面に使う幾何公差｜線の輪郭度／面の輪郭度の使い方

曲線や曲面に使う幾何公差である輪郭度公差とは？

幾何公差に関する前回の記事では、「振れ公差」の種類や特徴、使い方を説明しました。
今回は、主に曲線や曲面を規制する「輪郭度公差」について解説します。

１．輪郭度公差とは
- 輪郭度公差の種類
２．線の輪郭度
３．面の輪郭度
４．輪郭度公差を使う際の注意点

１．輪郭度公差とは

「輪郭度公差」は、主に真っすぐでない線や面（曲線や曲面）などを正確に作って欲しい場合に使われる幾何公差です。特徴的なのが、形状公差や姿勢公差(*)、位置公差としても使えることです。姿勢公差や位置公差として使う場合は、データムを指定する必要があります。

(*)姿勢公差として使う機会は少ないため、本記事では形状公差と位置公差としての使い方のみご紹介します。

輪郭度公差の種類

表1のように、輪郭度公差には2つの種類があります。

【表1　輪郭度公差の種類】

なお、線の輪郭度は使用頻度が少ないので、本記事では面の輪郭度について多く説明をしています。
それでは、2つの輪郭度公差について解説していきます。

２．線の輪郭度

（1）線の輪郭度とは

「線の輪郭度」は、指示した曲線であって欲しいと形体に対して指示する幾何公差です。
線の輪郭度で規制できる形体は、対象表面における1本の自由曲線であり、図1に示すように、その曲線を挟む2曲線間などが公差域になります。

【図1　線の輪郭度の公差域】

（2）形状公差としての線の輪郭度の使い方

まず、「形状公差」としての線の輪郭度の使い方を解説します。

① 部品上面への線の輪郭度指示

上面に曲面を持つ部品を考えます。上面における曲線形状が正確になって欲しい場合を想定し、理想形状からのズレは、その中心からそれぞれ0.05mm（幅0.1mm）まで許容できるとします。

この場合、表面上の任意の位置にある1本の曲線が規制対象です。
そのため、図2のように輪郭を示す寸法線からは外した位置へ線の輪郭度を指示してください。

また、線の輪郭度を使う際は、理想的な曲線であることを示す「理論的に正確な寸法（※以下、理論寸法と記述）」を用います。したがって、輪郭を示す寸法は四角で囲む必要があります。
公差域は、この理論寸法を中心に公差値を均等に割った領域となるため、公差値の前にφは付けません。

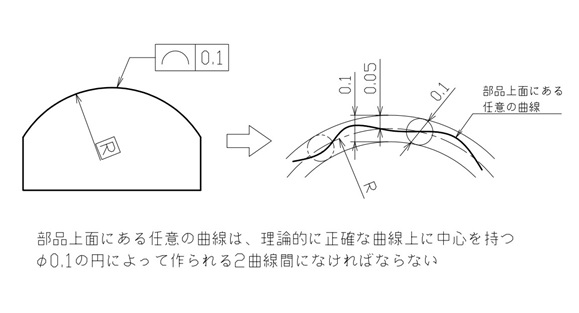
【図2　線の輪郭度の図示例と解釈①】

② 部品全周への線の輪郭度指示

では、同じく上面に曲面を持つ部品において、上面だけでなく部品全周にわたって線を規制したいケースはどうなるでしょうか？

この場合は、図3のように、公差記入枠と結ばれる引き出し線の折れ曲がり部を円で囲んでください。これが全周指示を示す記号になります。
また、形状を示す寸法は四角で囲む必要があります。

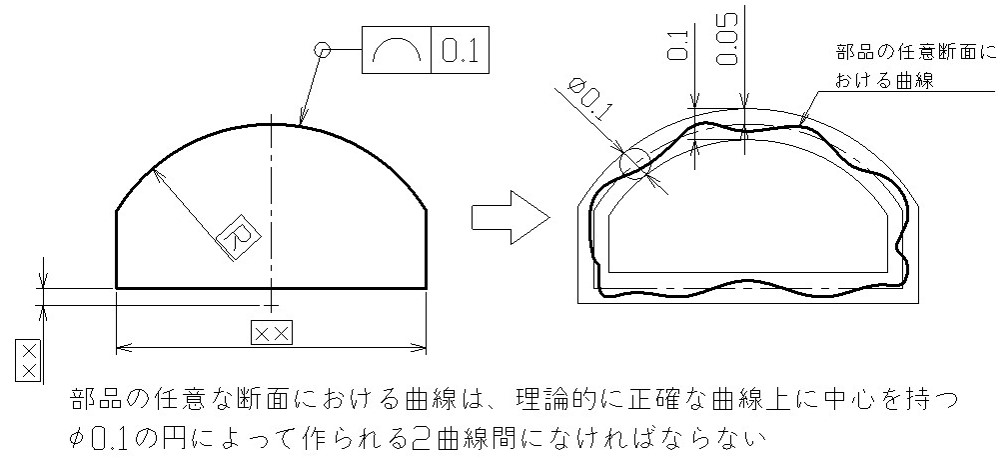
線の輪郭度の図示例と解釈②v2
【図3　線の輪郭度の図示例と解釈②】

（3）位置公差としての線の輪郭度の使い方

次に、位置公差としての線の輪郭度の使い方を解説します。
位置公差として使う場合は、設計者が意図する曲線の形状に加え、その曲線の位置も規制することになります。

《平面を基準とした際の、部品上面への線の輪郭度指示》

ある基準面から正確な位置に、理論寸法通りの曲線があって欲しい場合を想定。目標とする曲線からのズレは、理論寸法の中央からそれぞれ0.05mmまで許容できるとします。

この場合は、図4のように基準となる面へデータムを指定し、規制対象となる上面の曲線には、輪郭を示す寸法線からは外した位置に線の輪郭度を指示してください。
輪郭を示す寸法と位置を示す寸法は理論寸法のため、四角で囲みます。

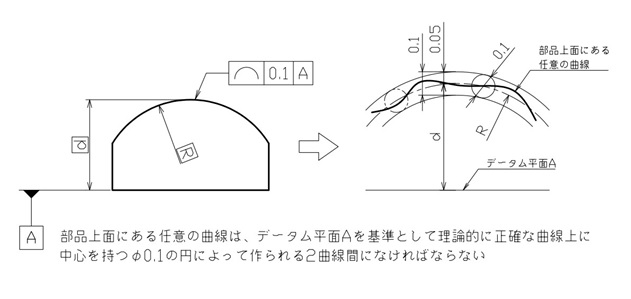
【図4　線の輪郭度の図示例と解釈③】

３．面の輪郭度

（1）面の輪郭度とは

「面の輪郭度」は、指示した曲面であって欲しいと形体に対して指示する幾何公差です。
面の輪郭度で規制できる形体は1枚の自由曲面であり、図5のように、その曲面を挟む2枚の曲面間が公差域になります。

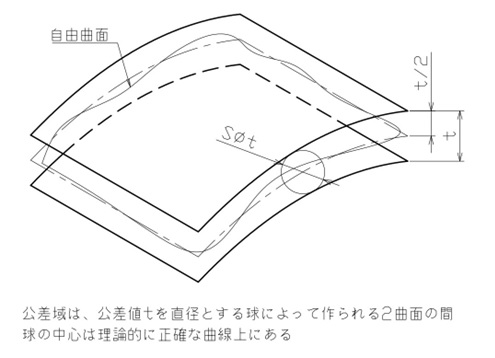
【図5　面の輪郭度の公差域】

（2）形状公差としての面の輪郭度の使い方

まず、形状公差としての面の輪郭度の使い方を解説します。

① 部品上面への面の輪郭度指示

上面に曲面を持つ部品において、正確な曲面が欲しい場合を想定。理想的な曲面からのズレは、理論寸法の中央からそれぞれ0.05mmまで許容できるとします。

この場合は図6のように、輪郭を示す理論寸法からは外した位置に面の輪郭度を指示してください。
輪郭を示す寸法は理論寸法のため四角で囲みます。線の輪郭度のときと同様に、公差域は理論寸法を中心に公差値を均等に割った領域となるので、公差値の前にφは付けません。

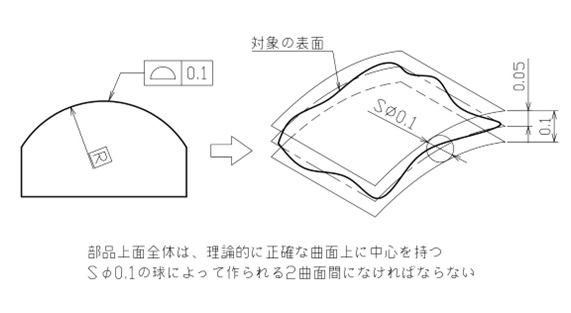
【図6　面の輪郭度の図示例と解釈①】

② 表面全周への面の輪郭度指示

また線の輪郭度と同様に、面の輪郭度は部品全周に対して適用できます。

図7のように、中央に四角い穴のあいたプレート部品で、この穴の表面が全周にわたって、正確な曲面であって欲しい場合を想定します。理想的な曲面からのズレは、理論寸法の中央からそれぞれ0.05mmまで許容できるとします。

この場合、規制対象となる穴の表面に対し、輪郭を示す理論寸法から外して面の輪郭度を指示してください。輪郭を示す寸法は四角で囲みましょう。
表面全周にわたり規制するので、引き出し線の折れ曲がり部へ全周指示の記号を付けます。

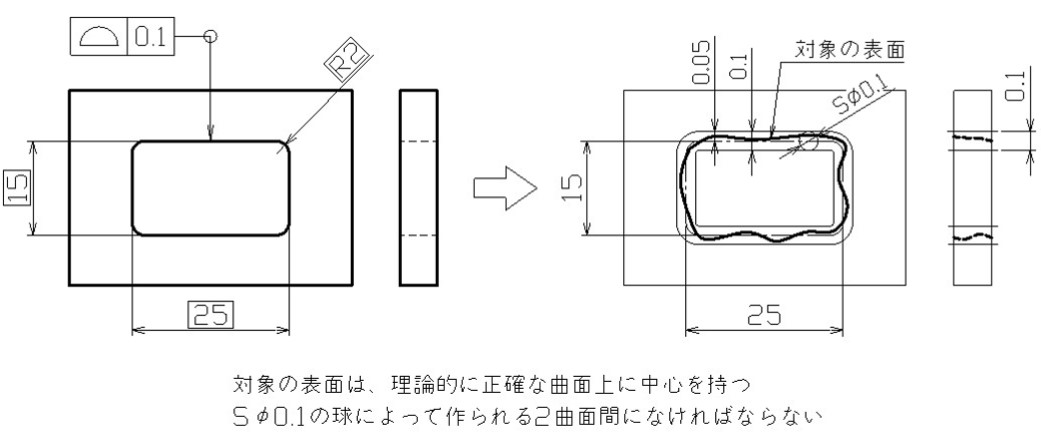
面の輪郭度の図示例と解釈②v2
【図7　面の輪郭度の図示例と解釈②】

（3）位置公差としての面の輪郭度の使い方

次に、位置公差としての面の輪郭度の使い方を解説します。

① 平面を基準とした際の、部品上面への面の輪郭度指示

ある基準面から正確な位置に、理論寸法通りの曲面があって欲しい場合を想定します。理想的な曲面からのズレは、理論寸法の中央からそれぞれ0.05mmまで許容できるとします。

この場合は図8のように、基準となる面へデータムを指定し、規制対象となる上面には、輪郭を示す寸法線からは外した位置に面の輪郭度を指示します。理論寸法のため、輪郭を示す寸法は四角で囲んでください。

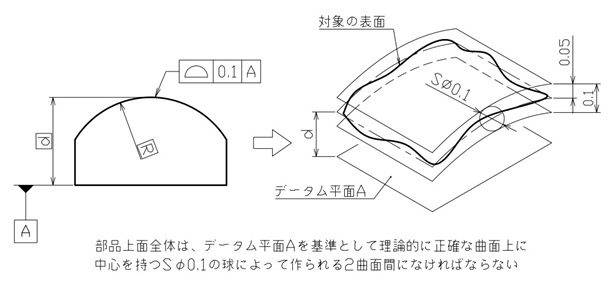
【図8　面の輪郭度の図示例と解釈③】

② 姿勢や位置も規制したい場合の、表面全周への面の輪郭度指示

図7の図面指示では、プレート部品にあいた穴の形状を規制できても、位置まで規制することはできません。
つまり、図7の図面指示を図9のように解釈することもできます。

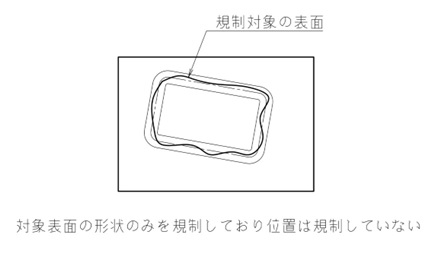
【図9　図7の図面指示における補足的な解釈】

この穴の表面が正確な位置にもあって欲しい場合は、図10のようにデータム平面A、B、Cを指定するといいでしょう。

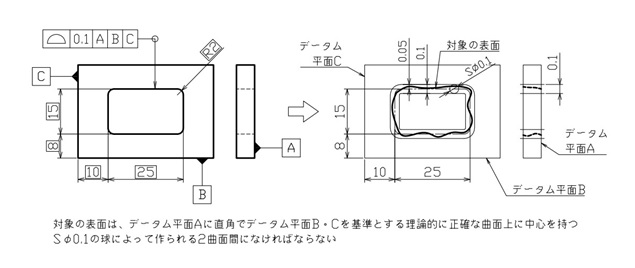
【図10　面の輪郭度の図示例と解釈④】

４．輪郭度公差を使う際の注意点

輪郭度公差は曲線や曲面だけでなく、直線や平面、軸線や中心平面など、部品を構成するほぼすべての形体に適用できます。そのため、他の幾何公差の代用としても使われます。
例えば、面の輪郭度を、平面度や円筒度の代わりに使うことが可能です。
図11と図12に、それぞれの例を示します。

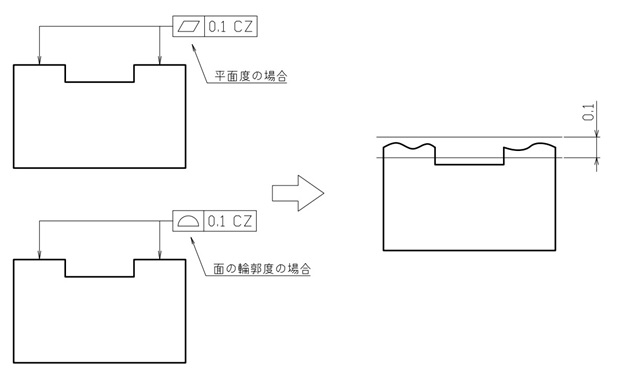
【図11　同じ公差域を示す2つの図示例①】

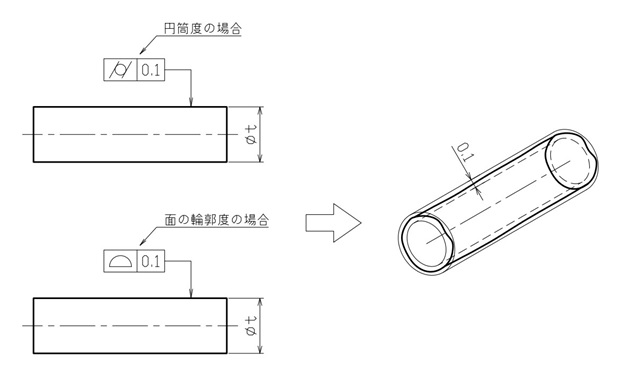
【図12　同じ公差域を示す2つの図示例②】

しかし、図面は「伝達手段」としての役割を持つため、設計意図を分かりやすく伝えることが求められます。
また、それぞれの幾何公差の名称や記号は「何を規制するのか」を端的に示すものがほとんどです。
そのため、輪郭度公差が他の幾何公差の代用になるからといって、多用するのは避けた方がいいでしょう。
設計意図を明確に伝えられるのはどの幾何公差かを考えて、公差の種類を選択してください。

以上、幾何公差の基礎知識や種類、使い方について全6回にわたり解説してきました。
幾何公差に苦手意識がある方も、この連載コラムを参考にしていただき、設計知識の向上に役立てていただければ幸いです。

また、アイアール技術教育研究所では本コラム以外にも、定期的に開催されるWebセミナーやeラーニング講座で、幾何公差を学ぶことができます。この機会にご利用してみてはいかがでしょうか？

（アイアール技術者教育研究所　Y・D)

《参考文献・サイト》