【機械設計マスターへの道】過渡応答を理解する [自動制御の前提知識]

Tweet

Pocket

前回コラムでは、伝達関数とブロック線図についてご説明しました。

今回は、「過渡応答」について解説します。
「過渡応答」とは、制御系に加えられる入力がある一定値の定常状態から別の状態に変化したとき、出力が変化後の定常状態に落ち着くまでの動きのことで、自動制御を考えるうえで重要な現象の一つです。

１．過渡応答の種類

過渡応答には次の3種類があります。
 

（1）インパルス応答

系に瞬間的な、入力変化（インパルス）が与えられたときの出力応答のことです。
 

（2）ステップ応答

系にステップ状の入力（ステップ関数）が与えられたときの出力応答をいいます。特に単位ステップが加わった場合を「インディシャル応答」と呼びます。
工業的に重要で、実験的にも実現しやすいため、一般的に応答特性の評価に使用されます。
 

（3）ランプ応答

y(t)=at(aは定数）のように、時間比例で増加する特性をランプ関数といい、ランプ関数状の入力に対する応答をランプ応答といいます。システム起動時の設計等に利用されます。

3種類の過渡応答の入力形態は、図1のようになります。

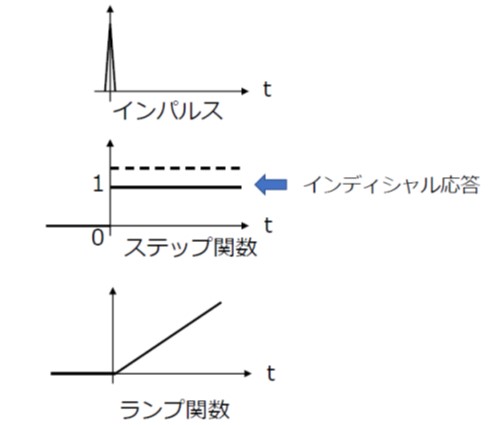
［図1　過渡応答の入力形態］

２．過渡応答に用いる指標

過渡応答中に生じる出力変化の状況を表す指標とその定義についてまとめると、次のようになります

• 遅れ時間： 出力xが変化後の定常値x0の50％に達するまでの時間
• 立ち上がり時間： 出力が変化後の定常値x0の10%になってから90％に達するまでの時間
• オーバーシュート： 出力xが変化後の定常値x0を一次的に超えて最初に達する極大値
• 行き過ぎ時間： オーバーシュートにおける最初の極大値に到達するまでの時間
• 整定時間： 変化後の定常値x0の±5％以内に収まるまでの時間

各指標についてステップ応答を例にとると、図2のようになります。
［①遅れ時間、②立ち上がり時間、③オーバーシュート、④行き過ぎ時間、⑤整定時間］

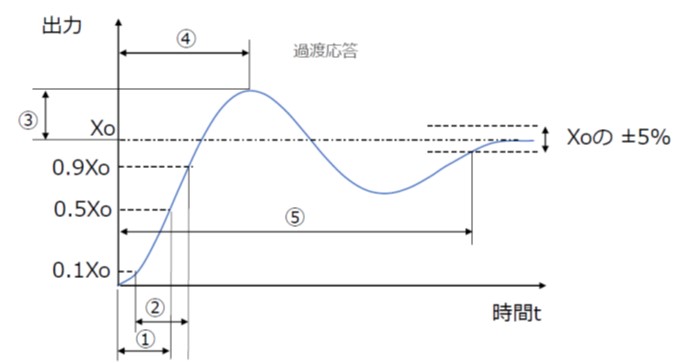
［図2　過渡応答の用語］

３．過渡応答の例

いくつかの基本要素について工業的に重要なステップ応答特性を考えてみます。
 

（1）1次遅れ要素

前回のコラムより、1次おくれ要素の伝達関数は、

また、前々回コラム中の表より、単位ステップ関数のラプラス変換は、

したがって、
出力　　　　・・・（1）
となって、応答特性は図3のような指数関数曲線となります。

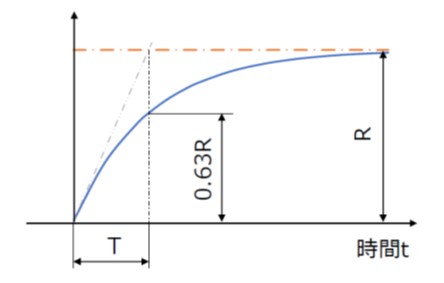
［図3　1次おくれ要素のステップ応答］

ここで原点における変化割合は、

式（1）で t=T とおけば、
　x = R(1-e^-1) ≒ 0.63

つまり、時定数は原点における接線が定常値と交わるまでの時間であって、応答曲線が定常値の63％に達するまでの時間、ということになります。
 

（2）積分要素

前回コラム（「伝達関数とブロック線図」のページを参照）より、積分要素の伝達関数は、

単位ステップ関数のラプラス変換は、

であることより、

出力　

したがって、応答特性は図4のような勾配R/Tの直線となります。

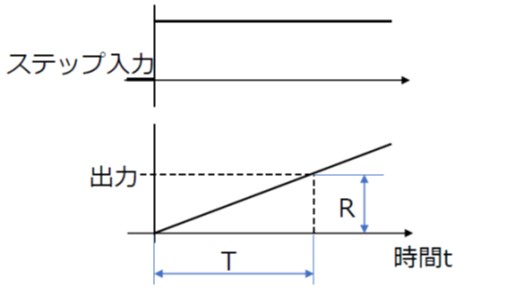
［図4　積分要素のステップ応答］

（3）1次遅れ微分要素

前回コラムより、1次遅れ微分要素の伝達関数

単位ステップ関数のラプラス変換は、

であることより、
出力　

応答特性は図5のように時間とともに減衰する指数関数となります。

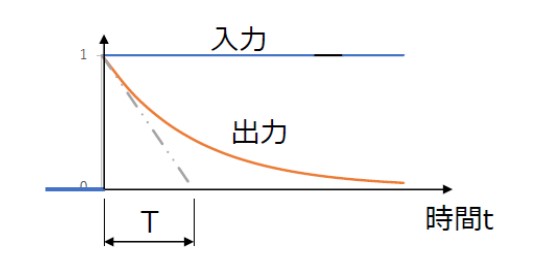
［図5　1次おくれ微分要素のステップ応答］

この要素は、入力の微分値に対する1次遅れの応答を示すということができ、「微分回路」と呼ぶことがあります。
 

（4）振動系2次要素

系の安定性

伝達関数の分母＝0 とおいた式を、「特性方程式」といいます。
制御系が安定であるためには。特性方程式の根（「極」といいます）の実数部がすべて負であることが必要です。0である場合は、安定不安定の境界となり、実数部が正の場合、出力が時間とともに増大して不安定となります。

前回コラム（「伝達関数とブロック線図」のページを参照）より、振動系2次要素の伝達関数は
　

特性方程式　

「極」は、

したがって、系が安定であるためには ζ＞0 であることが必要となります。

特性方程式の根は、

• 0＜ζ＜1 のときは複素根を持ち、減衰振動となります。
• ζ＝1 のときは等根となって、この状態を「臨界減衰」といいます。
  この時の過渡応答特性は　x(t) = R { 1- (1 + ω_nt) e^-ωnt}　で表されます。
• ζ＞1 のときは実根をもち、過減衰(非振動状)となります。
  ζ の大小による過渡応答特性曲線は、図6のようになります。

なお、ζ＝0 のときは無減衰となって、振動が継続する状態になります。
ζ＜0 のときは振動が発散する負性減衰となって、系は不安定となります。

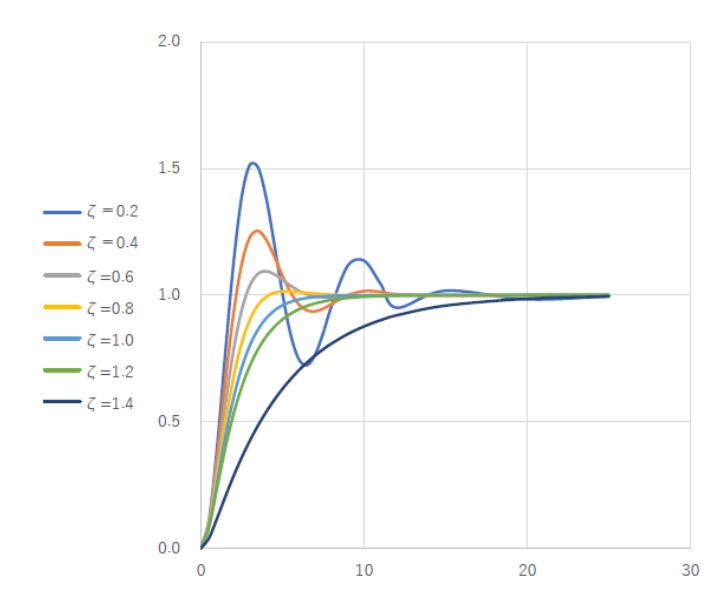
［図6　振動系2次要素のステップ応答］

以上、今回は「過渡応答」についてご説明しました。

次回は、周波数応答とBode線図について解説したいと思います。

（日本アイアール株式会社　特許調査部　S・Y）
 

Tweet

Pocket