【機械設計マスターへの道】伝達関数とブロック線図 [自動制御の前提知識]

Tweet

Pocket

前回の当連載コラムでは、フィードバック自動制御を理解するうえで必要となる数学的な基礎知識（ラプラス変換など）についてご説明しました。

今回は続きとして、ラプラス変換された入力出力特性から制御系の伝達特性を代数方程式で表す「伝達関数」と、入出力及びフィードバックの流れを示す「ブロック線図」について解説します。
 

１．伝達関数

出力をラプラス変換した値と、入力をラプラス変換した値の比のことを、要素あるいは系の「伝達関数」といいます。

入力をy(t)、そのラプラス変換を ℒ[y(t)]=Y(s)
出力をx(t)、そのラプラス変換を ℒ[x(t)]=X(s) とすれば、
　伝達関数G(s)=X(S)/Y(S)　　(出力X(s)=G(s)・Y(s))
ただし、入力、出力ともに初期値をゼロとします。

例として、入力に単位ステップ信号を加えた場合は、前回コラムで紹介した変換表より Y(S)=1/s ですから、出力（応答）は X(s)=G(S)/s
これをラプラス逆変換して、時間応答は　x(t) = ℒ-1[G(S)/s]　
となります。

一般に要素や系の動特性は、エネルギや物質収支の時間変化を考えた微分方程式で表現されますが、これをラプラス変換することにより、単純な代数方程式の形で伝達関数を求めることができます
 

２．ブロック線図

ブロック線図は、制御系における信号伝達の経路や伝達状況を視覚的にわかりやすく示すために用いられる図です。

要素を四角い枠で囲み、その中に要素の名称や伝達関数を記入します。
また、信号の経路を直線で示し、信号の流れる方向に矢印をつけます。
さらに、図のような加え合せ点（あるいは集合点）や引出し点が使用されます。
加え合せ点では信号の和には+、差には‐の記号を付します。
 

（1）ブロック線図の結合法則

① 直列接続

直列に接続した複数の要素を信号が順次伝わる場合です。
図1の例では

G1,G2を一つにまとめた伝達関数は、

となります。

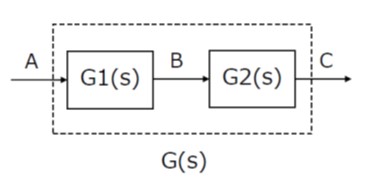
［図1　ブロック線図の直列接続］

② 並列接続

一つの信号が複数の要素に並行して加わる場合です。
図の例では

D = B±C = (G1±G2)A

したがって全体の特性を表す伝達関数は

となります。

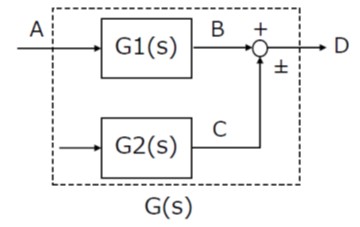
［図2　ブロック線図の並列接続］

③ フィードバック接続

図3の例で、信号Cは加え合せ点により C = A±B
出力Dは、D=CG1, B=DG2 の関係があります。

したがって D = (A±B)G1 = G1A±BG1 = G1A±DG1G2 = G1(A±DG2）

全体の特性を表す伝達関数は、

上式を整理して　

となります。
複合は加え合せ点の符号と逆になることに注意が必要です。

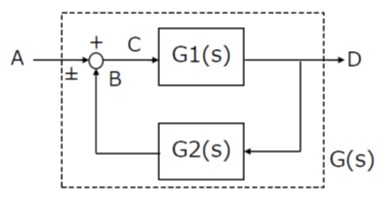
［図3　フィードバック接続］

（2）等価変換の原則

ブロック線図の加え合せ点や引出し点を、要素の前後に移動した場合の、伝達関数の変化については、図4のような関係があります。
直列接続、並列接続、フィードバック接続の伝達関数の結合法則を理解した上で、必要に応じて等価変換を行うことにより複雑な系のブロック線図を整理して、伝達関数を求めやすくすることができます。

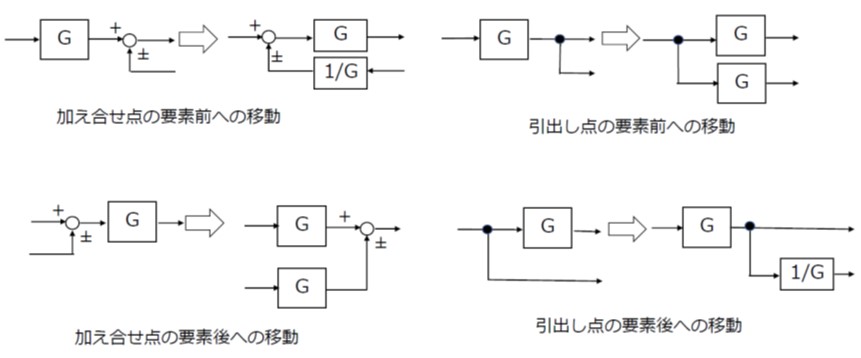
［図4　ブロック変換の等価変換の例］

３．基本的要素の伝達関数

機械の自動制御を考えるとき、機械の動作や、それに伴って起きる現象は、いくつかの基本的な関数で表されることが多くあります。いくつかの基本要素と、その伝達関数について考えてみます。
 

（1）1次遅れ要素

伝達関数が で表される系を「1次遅れ要素」といいます。

ここで、Rをゲイン定数、Tを時定数、といいます。

1次遅れ要素は、容量と抵抗の組合せによって生じます。

機械系の例として、図5(a)のようなタンクに水が流出入する場合の液面変化、(b)のように部屋をヒータで加熱する場合の温度変化、などの伝達関数を求める場合に適用することができます。

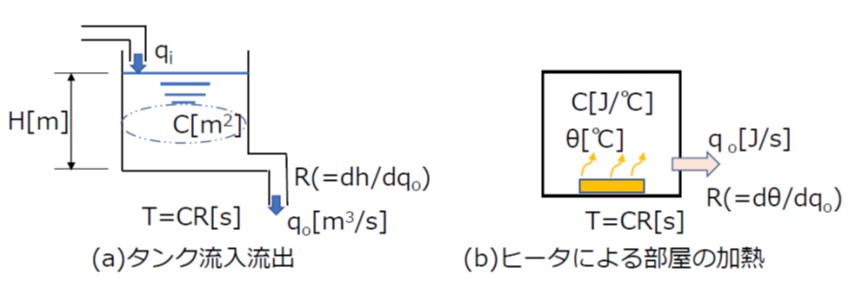
［図5　1次遅れ系の例］

（2）振動系2次要素

図6のように、質量m、減衰係数c、ばね定数k からなる減衰のある1自由度線形振動系において、質点の変位x、外力yの関係は、下記の微分方程式で表されます。

このような振動系2次要素の伝達係数は、次の式で表されます。

ζ は「減衰比」とよばれる値で、下記の式で表されます。

ωn は「固有角周波数」で、下記の式で表されます。　　

時定数T = 1/ ωn と定義すれば、上の式を一般化して

と表すことができます。

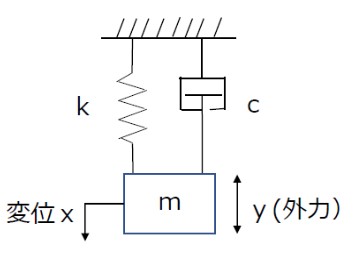
［図6　1自由度線形減衰強制振動系］

（3）1次遅れ微分要素

ダッシュポットとばねを組み合わせた振動減衰装置などに適用されます。

図7の系の運動方程式は次式になります。
ただしyは入力としてのピストンの動き、xは応答としてのシリンダの動きです。

ここでk：ばね定数、c：減衰係数、時定数T=c/k と定義すれば
伝達関数
となります。

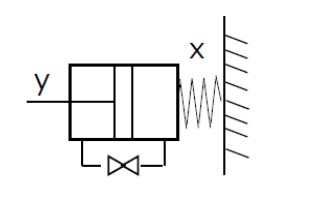
［図7　一次遅れ微分要素の例（ダッシュポット）］

（4）むだ時間要素

図8のように長い管路で流体をタンクへ移送する場合など、注入点から目的地点までの移送時間による時間遅れが生じます。
注入点における入力をf(t)とすれば、目的地点ではf(t-L)で表すことができます。

ただし L=ℓ/v
ℓ：注入点から目的地までの距離
v：管路内の流速
この場合の伝達関数は G(s) = e^-Ls となります

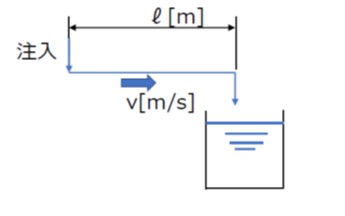
［図8　むだ時間要素の例（管路）］

以上、今回は伝達関数とブロック線図について説明しました。
次回は、過渡応答について解説します。

（日本アイアール株式会社　特許調査部　S・Y）
 

Tweet

Pocket