周波数応答・周波数伝達関数を解説！ボード線図って何？

Tweet

Pocket

前回コラムでは、自動制御を理解する上での前提知識として「過渡応答」についてご説明しました。

今回は、周波数応答の基礎知識とボード線図について解説します。

１．周波数応答と周波数伝達関数

線形で安定した制御系に、振幅A、角周波数ωの純正弦波 y(t)=Ae^jωt が入力として与えられたとき、過渡的には乱れが生じても、系が安定していれば、過渡成分は消滅して、応答出力は入力と同じ周波数の正弦波となって、振幅と位相が周波数に依存して異なる特性となります。これを「周波数応答」といいます。

周波数応答を解析するとき、ｓをjωで置き換えた伝達関数G(jω)を用います。
G(jω)のことを「周波数伝達関数」といいます。
入力と出力の関係は図1のようになります。

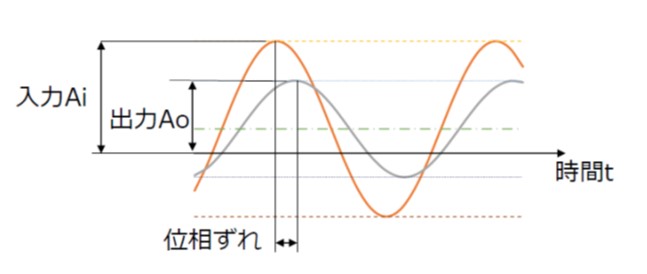
【図1　周波数応答】

２．周波数特性とゲインおよび位相

周波数伝達関数をG(jω)、入力を A_ie^jωt とすれば、

ここで Ao/Ai は入出力の振幅比、ψ は位相ずれを示します。

入力正弦波の角周波数ωを変えると、出力正弦波の振幅Aoおよび位相ずれψが変化し、振幅比と位相ずれはωの関数となります。

G(jω)は、ωの複素関数であることから
G(jω) = Re(ω)+j Im(ω) = |G(ω)｜∠G(jω)

したがって、次のようになります。

振幅比|G(ω)｜のことを「ゲイン」と呼びます。
ゲインと位相ずれを角周波数ωの関数として表したものを「周波数特性」といいます。

３．1次おくれ要素、振動系2次要素の周波数特性

（1）1次遅れ要素

一般化した1次おくれ要素の伝達関数

においてs=jωとおき、共役複素数を用いて分母を有理化すれば

よって、次のようになります。

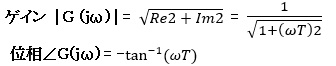
（2）振動系2次要素

一般化した振動系2次要素の伝達関数

において、s=jω、ωT=uとおいて、1次おくれ要素と同様に整理すれば、次のようになります。

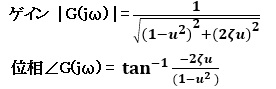
４．ボード線図（Bode線図）

周波数応答を図に表す方法として、よく使われるものに「ボード線図」（Bode線図）があります。
角周波数ωを横軸に対数目盛でとり、
ゲインを対数量 20log₁₀|G(jω)|(dB)で表して、位相ずれ（度）とともに縦軸にとった線図を「Bode線図」といいます。

ボード線図は、次のような利点（メリット）があります。

• ゲインを対数量で表すため、要素の積を代数和で求めることができて、複数要素の組合せ特性を求めるのにも便利
• 対数目盛を用いるので、広範囲の周波数に対応できる

1次おくれ要素と、2次おくれ要素のボード線図は図2，3のような特性となります。

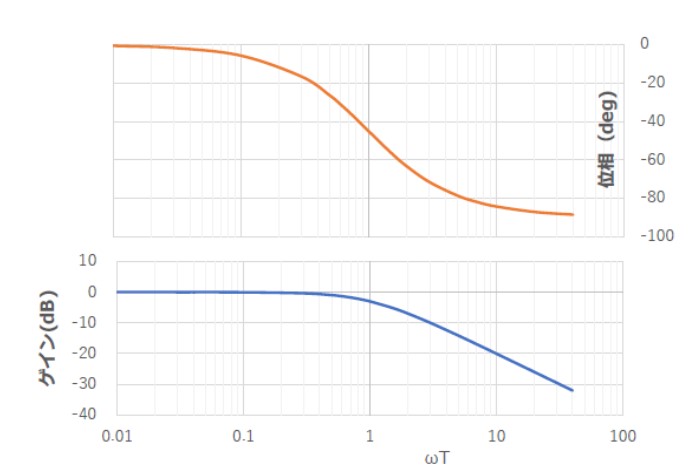
【図2　1次おくれ要素のボード線図】

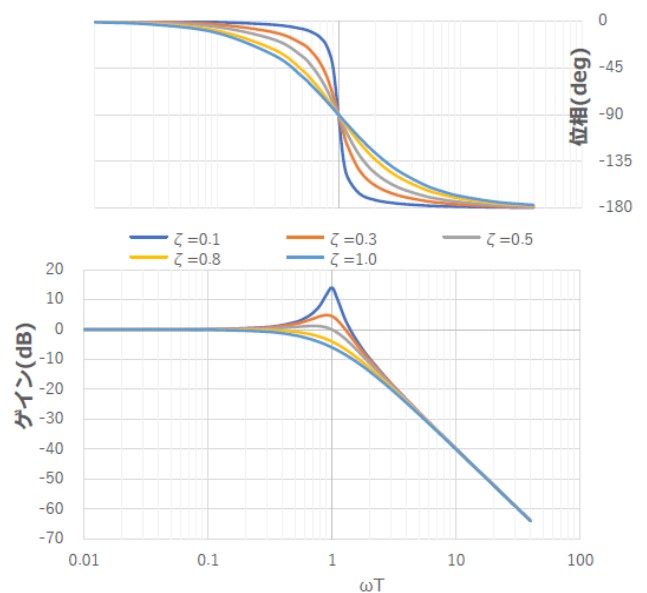
【図3　振動系2次要素のボード線図】

５．一巡伝達関数とゲイン余裕

当連載の「伝達関数の求め方とブロック線図をわかりやすく解説！」の回で説明したフィードバック接続のブロック線図において、制御対象伝達関数G1(s)とフィードバック伝達関数G2(s)のsをjωで置き換えたとき、
G(jω) = G1(jω)・G2(Jω) を「一巡周波数伝達関数」といいます。

図4のように一巡周波数伝達関数の周波数特性をボード線図で表したとき、ゲインが1(0dB)となる角周波数において、位相が-180°に対してどれほど余裕があるかを示す値を「位相余裕」といいます。
また、位相が-180°となる角周波数において、ゲインが１(0dB)に対してどれほど余裕があるかを示す値を「ゲイン余裕」といいます。系が安定であるためにはゲインが1.0(0dB)以下である必要があり、ゲイン余裕が大きいほど安定性が増します。

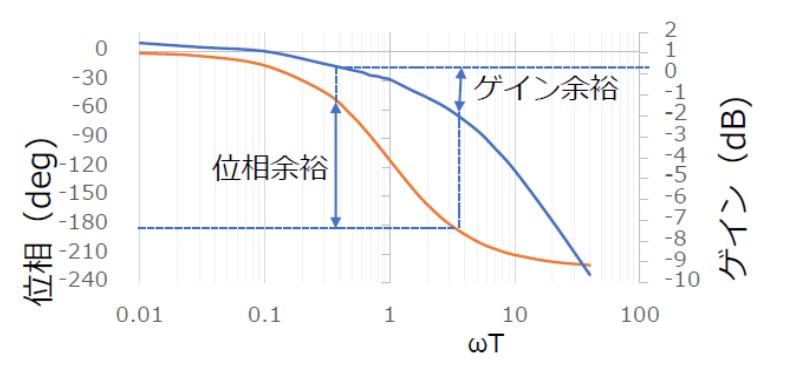
【図4　振動系2次要素のボード線図】

以上、今回は周波数応答とボード線図についてご紹介しました。

次回は、プロセス制御によく用いられるPID制御についての解説です。

（日本アイアール株式会社　特許調査部　S・Y）
 

Tweet

Pocket