【機械設計マスターへの道】自動制御を理解するために必要な数学的基礎知識 (ラプラス変換など)

Tweet

Pocket

前回コラムでは、自動制御の分類とフィードバック制御の特徴、構成などの概要をご紹介しました。
今回は、フィードバック自動制御を理解するうえで必要となる数学的な基礎知識について解説します。
 

１．複素数と複素平面

ｘ、ｙを実数としたとき、
下記の式で表されるzのことを複素数といいます

　ｚ=x + jy　　　・・・(1)

ここで、ｊのことを「虚数単位」といい、
2乗するとマイナス1となる実在しない仮想の数で、で定義されます。

数学では虚数単位の記号として i を用いますが、電流とまぎらわしいため、工学では j を用います

(1)式の右辺第1項を「実部」（Real part）、第2項を「虚部」（Imaginary part）と呼び、
それぞれ x=Re(z),y=Im(z) で表します。

実部を横軸に、虚部を縦軸にとり、直角座標平面に複素数ｚを表します。
x軸を実軸、y軸を虚軸とする平面を「複素平面」または「ガウス平面」といいます。

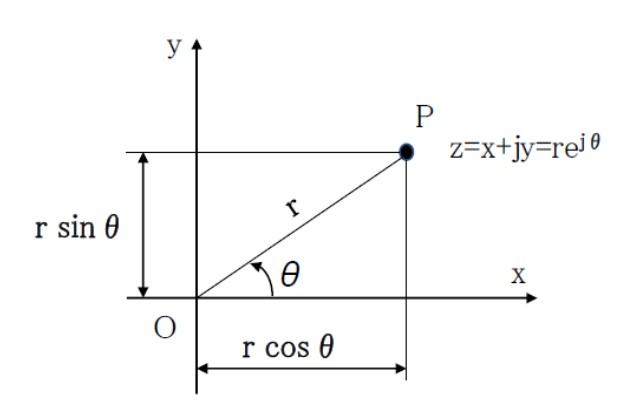
［図1 複素平面（ガウス平面）］

x+jy , x-jyという、複素平面の実軸に対して対称な2つの複素数のことを「共役複素数」といいます。
図1で座標原点と点Pを結ぶ線分の長さr、線分OPの正の実軸から反時計回りになす角度θは、下記のようになります

θ=tan^-1(y/x)

rを複素数zの絶対値、θを複素数の偏角といいます。
偏角はarg(z)または∠zと書きます。

幾何学的関係から、x=r cos⁡θ ,y=r sin⁡θ　となりますから、前の（1）式は、次の(2)式のように表すことができます。

　z=r(cos⁡θ + jsin⁡θ)　　　・・・(2)

ここで、オイラーの公式 e^jθ= cos⁡θ + j sin⁡θ より、(2)式は次のように表されます。

　z=r e^jθ　　　・・・(3)

すなわち複素数は極座標（r,θ）を用いて指数関数で表すことができます。

ここでe=2.718281828459…
eは「ネイピア数」と呼ぶ無理数で、自然対数の底です。

複素数を(3)式の形で表すことで、自動制御では、後ほどの解説中に登場する周波数応答を考えるうえで有用となります。
 

２．ラプラス変換

制御系では各種の信号が各要素を通過して流れていきます。
要素、あるいは制御系の特性はそれに加わる入出力信号と、その信号に対する要素や制御系の応答によって知ることができます。
つまり入出力の伝達特性を調べることが重要となります。

「ラプラス変換」は、制御系における入出力間の伝達特性を調べるときに用いられる数学的な変換手法です。
各種工業プロセスやサーボ機構において、制御対象の特性はある時間関数f(t)の形で表されます。
次の式で表されるF(s)をf(t)のラプラス変換といいます。

　　　・・・(4)

ここで、sは複素数です。
f(t)を「原関数」、 F(s)を「像関数」といいます。

また、 F(s)をf(t)に変換することを「ラプラス逆変換」といい、次のように定義されます。

　　　　・・・(5)

bは正の定数で、積分路は複素平面にて b-j∞ から b+j∞ までをとります。

F(s)とf(t)との関係はいちいち計算するよりも、変換表があるので、これを利用したほうが便利です。
表1は、代表的な関数とそのラプラス変換の換算対応表です。

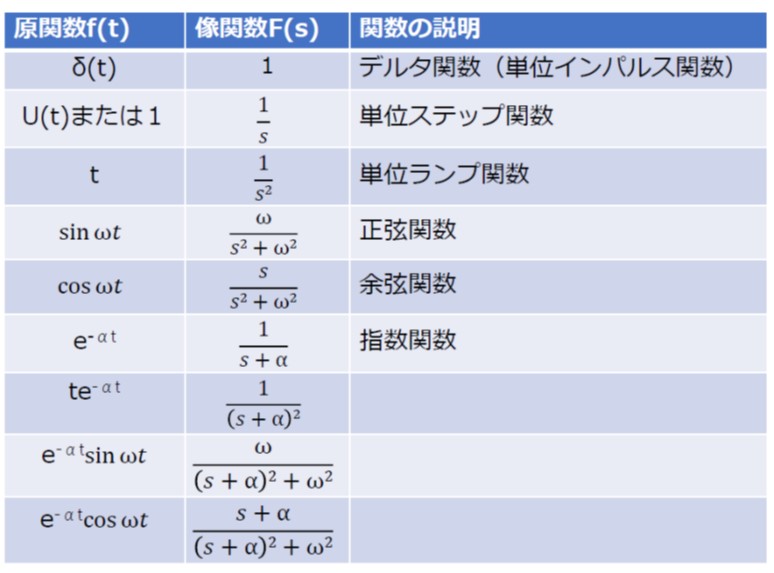
［表1　主要な原関数のラプラス変換］

ラプラス変換された像関数F(s)を部分分数に分解することにより、上記の変換表に当てはまる像関数の組合せに変形することができて、原関数(t)を求めることができる場合が多くあります。
 

ラプラス変換の重要定理と利点

（1）
　ℒ[A₁f₁(t) + A₂f₂(t)] = A₁F₁(s) + A₂F₂(s)　　※A₁、A₂は定数

これはラプラス変換しても線形性が維持されることを示します。
 

（2）

一般に の関係があります。
 

（3）

一般に の関係があります。
 

ただし （2）（3）においては、初期値をすべてゼロとしています。
初期値をゼロとみなすことができる場合は、時間関数の微分方程式をラプラス変換することにより、簡単な代数方程式に置き換えることができ、信号の入出力の伝達特性を定量的に把握することが楽に行えるようになります。
 

次回の連載コラムでは、ラプラス変換された入力出力特性から制御系の伝達特性を代数方程式で表す「伝達関数」と「ブロック線図」（入出力及びフィードバックの流れを示す図）について解説します。

（日本アイアール株式会社　特許調査部　S・Y）
 

Tweet

Pocket