荷重、応力、ひずみの基本を整理！応力-ひずみ線図など重要知識をわかりやすく解説
機械には、さまざまな力が作用します。機械部材は力を受けて変形し、耐えられなくなると破壊します。
設計者は、変形量が所定の許容値内に収まり、破壊することがないように、機械に使用する部材の材料を選定し、形状と寸法を適切に決める必要があります。
そのために先ずは、荷重と応力の意味、その種類、応力とひずみについて理解する必要があります。
１．荷重の種類
機械の部材に外部から作用する力を「荷重」と呼びます。
荷重には次の5種類があります。
- 引張荷重：材料を引き延ばす方向に作用
- 圧縮荷重：材料を押し縮める方向に作用
- せん断荷重：材料を切断するような方向に作用
- 曲げ荷重：材料を曲げる（たわむ）方向に作用
- ねじり荷重：材料をねじる（ひねる）方向に作用
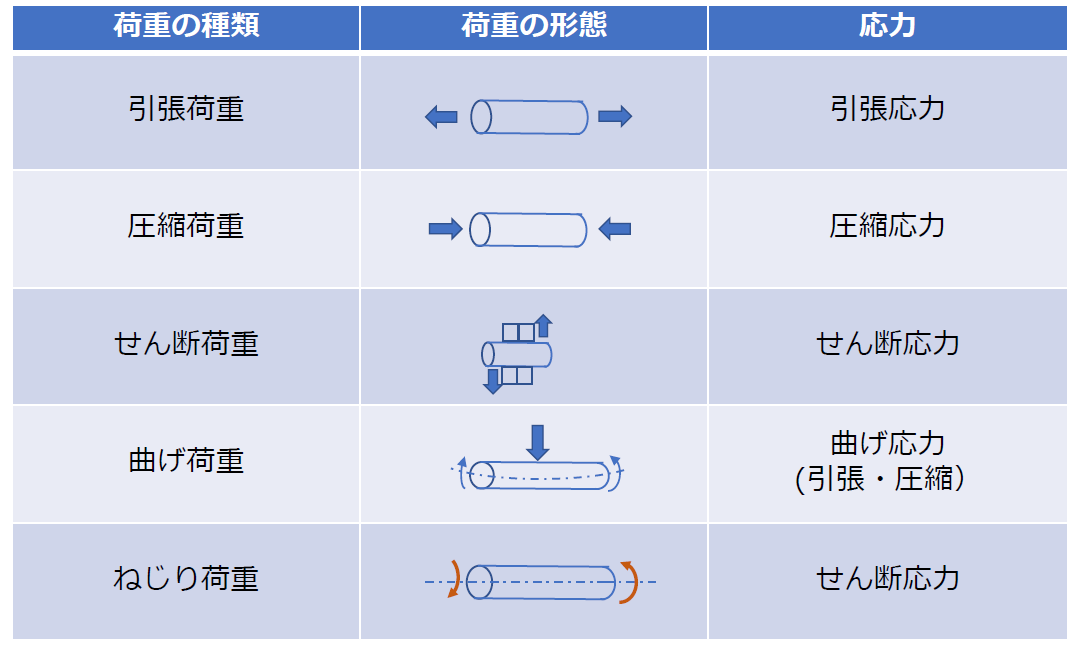
【表1 荷重の種類と応力との関係】
２．応力の基礎知識
① 垂直応力
部材に荷重が作用すると、部材には受ける荷重に等しい大きさの内力が発生します。
内力を内力の作用する方向に垂直な部材の断面積で割った値を「垂直応力」と呼び、ギリシャ文字σ（シグマ）で表します。
内力をF(N),断面積をA(mm2)とすれば、
応力σ=F/A(N/mm2=MPa)
垂直応力には「引張応力」と「圧縮応力」があります。
引張荷重の場合は引張応力となり、圧縮荷重の場合は圧縮応力となります。
② せん断応力
せん断荷重を受けるときには、部材の断面と同じ方向に内力が発生します。
この時の内力を、内力と同方向の部材断面積で割った値を「せん断応力」と呼び、ギリシャ文字τ（タウ）で表します。
③ 曲げ応力
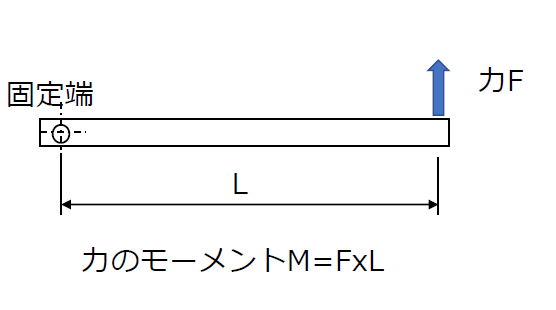
細長い形状の部材の一端を固定して他端に部材と直角方向の力を加えると部材は固定端を中心として回転しようとします。
固定端から力の作用点までの距離をＬ(mm)，力の大きさをＦ(N)とすれば、距離と力の積を「力のモーメントM」と呼び、モーメントMは、Ｍ=FxL (N-mm)で表すことができます。
はりや軸など細長い形状の部材の両端に大きさが等しく支点に対する方向が相反する力（「偶力」といいます）が作用すると、細長い部材は偶力により曲がろうとします。この偶力を「曲げモーメント」、曲げモーメントにより部材に発生する応力を「曲げ応力」と呼びます。
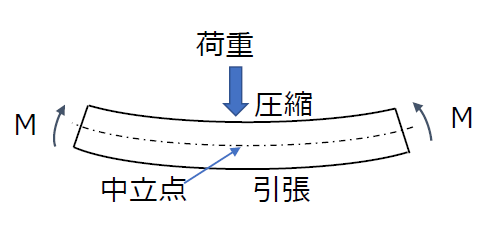
はりや軸に付加質量あるいは外荷重が加わると軸やはりはたわみ、付加質量や荷重は軸やはりに対し偶力となって作用して曲げモーメントを加えます。
はりに曲げが加わると図のように曲がった部材の凸側は引張応力、凹側は圧縮応力が作用します。
部材断面の中心には曲げ応力がゼロになる中立点が存在し、引張・圧縮応力は中立点から最も遠い表面で最大となります。
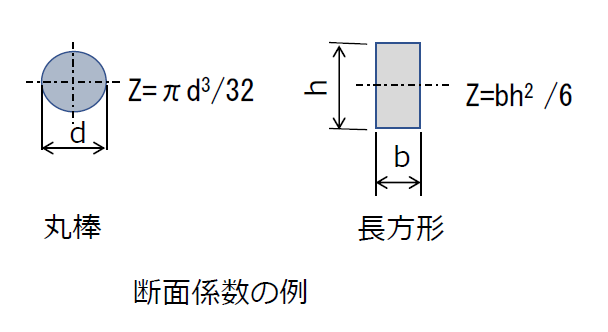
最大曲げ応力σbmaxは、曲げモーメントMを部材断面形状から求まる断面係数Z(mm3)で割ることで計算することができます。
最大曲げ応力 σbmax=M/Z(N/mm2=MPa)
なお、「断面係数」は、断面形状によって決まる値であり、曲げ荷重を受ける機械の構造強度を設計するうえで重要な係数となります。
<
［※関連記事：応力とは？｜引張応力/圧縮応力/せん断応力/曲げ応力の概要と求め方 はこちら］
④ ねじり荷重に対する応力
丸棒の一端を固定して、他端に偶力を加えて棒をねじる場合を考えます。
このとき、棒はねじりにより変形するので断面にはせん断応力が生じます。
偶力によるねじりモーメント（トルク）をT(N-m)、丸棒の直径をd(mm)、偶力によるねじりで棒の断面に生ずるせん断応力をτ（タウ）とすると、次の関係があります。
τ=16T×1000/(πd3) (N/mm2)
軸に加わる動力をP(kW)、軸の回転速度をn(min-1) とすれば次のようになります。
T=60×1000×P/(2πn) (N-m)
３．ひずみと弾性係数、フックの法則
部材は荷重を受けると変形します。
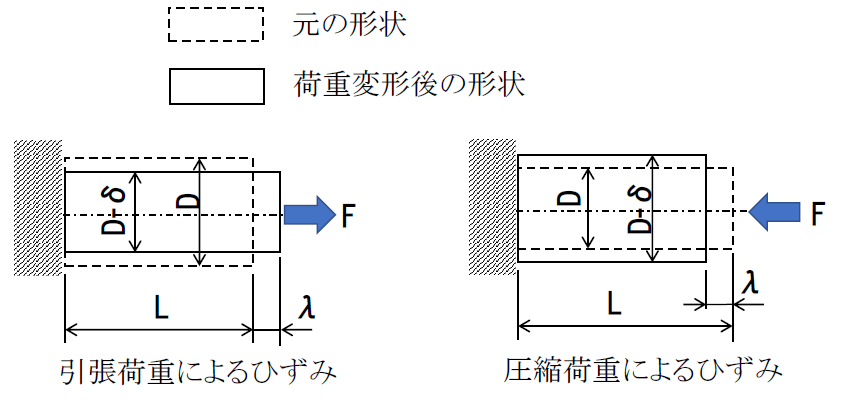
図のように、長さＬ、直径Ｄの丸棒に引張荷重Ｆが作用するときの棒の伸びをλ、直径の縮みをδとするとき、変形割合を表す量が垂直ひずみです。（圧縮荷重の場合は、長さが縮み、直径が太くなります）
縦ひずみ ε=λ/L
横ひずみ ε’=-δ/D
［※関連記事：ひずみとは？縦ひずみ/横ひずみ、せん断ひずみの求め方、式・記号などを解説 はこちら］
縦ひずみと横ひずみの比に負号つけた値を「ポアソン比」と呼び、ギリシャ文字ν（ニュー）で表します。
ポアソン比 ν =- ε’/ε
［※関連記事：ポアソン比の基本はこれを読めばOK！ はこちら］
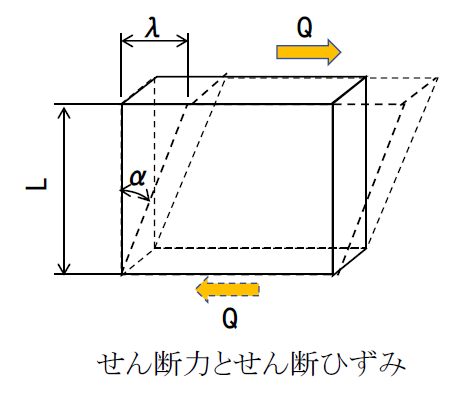
せん断力が加わる場合は下図のように考えます。
距離L離れたせん断力Qによって相対的なずれがλ生じたとすると、せん断ひずみγは
γ=λ/L=tan α
変形はごく小さいので tanα≒α よってγ≒α
部材に荷重が加わると部材内部に応力とひずみが生じます。ある限度までの荷重であれば荷重が除かれるとひずみはゼロに戻ります。このような変形を「弾性変形」といいます。
弾性変形範囲では、垂直応力と垂直ひずみ、せん断応力とせん断ひずみは、それぞれ比例します。
これを「フックの法則」と呼び、次式で表されます。
σ=Eε τ=Gγ
比例定数Eを縦弾性係数（ヤング率）、Gを横弾性係数、と呼びます。
EとGの単位は応力と同じですが、数値が大きいため通常はMPaではなくG（ギガ）Paを用います。
例えば、鉄鋼材料のヤング率は鋼種によらず、ほぼ一定の値で約210GPaです。
ヤング率E，横弾性係数G，とポアソン比νの間には次の関係があります。
E=2G(1+ν)
［※関連記事：フック法則とは？ はこちら］
４．「応力‐ひずみ線図」とは
材料の強度を知るために、規定の寸法形状の試験片に引張荷重を加えて破断するまで荷重を増やしていく引張試験が行われます。
横軸にひずみ、縦軸に応力をとった図を「応力―ひずみ線図」と呼びます。
<
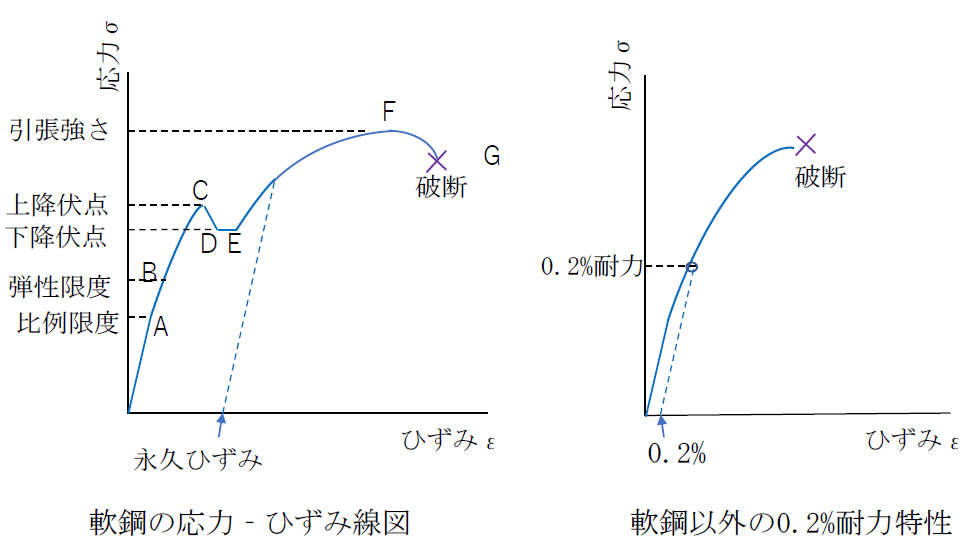
図の左は軟鋼の応力―ひずみ線図です
図のA点は弾性限度で0‐Aの間はフックの法則が成立し、直線の傾きがヤング率となります。
Aを超えて荷重を増やすと0－A間の比例関係は成立しなくなりますがB点までは荷重を0にすれば変形はなくなり、応力とひずみは0となります。B点を「弾性限度」といいます
Bを超えて荷重を増やすと、荷重を除いた後も部材は元の形に戻らず変形が残り、ひずみがゼロにはならなくなります。このような変形を「塑性変形」といいます。
変形は完全には元へ戻らずひずみが残留します。これを「永久ひずみ」といいます。
C点まで応力が上昇したあと応力はいったん低下しD～Eのような平衡状態を示します。
CからEに至る変形過程を「降伏」といいます。C点を「上降伏点」、DE部に相当する応力値を「下降伏点」と呼び、材料の機械的性質を表す指標の一つである降伏強さは下降伏点応力σYを採用します。
E点を超えて荷重を増大するとF点に達するまで応力が増大したあと、試験片にくびれが生じて断面積が急激に縮小して過重負担能力が急減少し、G点で破断します。
最高点Fに相当する応力を「引張強さ」と呼び、材料の機械的性質を表す重要な指標となります。
軟鋼以外では明確な降伏点が現れない材料が多く、図の右のように0.2%の永久ひずみが生じるような限界応力σ0.2を「0.2%耐力」と呼んで機械的性質の指標の一つとして利用します。
なお、試験片破断後の変形具合から伸びと絞りを求めます。伸びは試験片の伸び量をひずみ換算して％で表示したものです。絞りは破断後の最小断面積と元の断面積から算出した断面積減少率を％で表示したものです。
また、応力―ひずみ線図の線より下側の面積は、靭性（粘り強さ）すなわち材料が破壊するまでに必要なエネルギの大きさを表します。一般的に硬い材料は引張強さも大きくなりますが、ひずみが小さいために靭性は低くなる傾向があるので、靭性を必要とする機械材料を選定する際に注意が必要となります。
次回のコラムでは「強度設計の基礎知識」をご説明いたします。
（アイアール技術者教育研究所 S・Y)
