応力とは？ 引張応力/圧縮応力/せん断応力/曲げ応力の概要と求め方

Tweet

Pocket

「与えられた仕様と運転条件においては壊れることが無いように設計する」ということは、あらゆる機械に共通する課題です。今回は、設計する機械の頑丈さ（Robustness）を評価する上での基本的かつ重要な指標である「応力」について解説します。

１．応力とは（定義と単位）

機械には外部から様々な力（Force）が作用します。機械に加わる外力のことを「荷重」（load）といいます。
荷重の大きさだけでは、その機械がその荷重に対して壊れることなく運転できるのか否かを判定することはできず、機械部材の強さを考える上での共通指標で判断する必要があります。
その指標として荷重を受ける機械部材の単位面積当たりに発生する力のことを「応力」（stress）といいます。

応力を論じるときの面積の単位は[mm²]を用い、応力の単位は[N/mm²]（または[MPa]）となります。
応力は、簡単にいえば、”荷重を、その荷重を受ける部材断面積で割った値” のことですが、荷重と応力の種類によっては、もう少し複雑な計算によって求める必要があります。

２．応力の種類と求め方（応力計算の基本）

（1）引張応力とは

図1のような断面積A[mm²]の円柱の両端に、円柱を両側へ引き延ばそうとする方向に荷重Wt[N]が加わっているとします。このように部材を引き延ばそうとする方向に働く荷重を「引張荷重」、引張荷重を受ける部材に発生する応力を「引張応力」（tensile stress）といいます。
引張応力は部材の断面に対して垂直に作用します。このような応力を「垂直応力」といいます。
垂直応力を表す記号としてギリシャ文字のσ（シグマ）を用います。

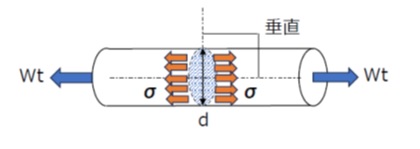
【図1　引張荷重と引張応力】

引張応力の求め方

図1の場合の引張応力は σ=Wt/A [N/mm²] となります。

円柱断面直径dが d=10[mm] であるとすれば、断面積 A=πd²/4=78.5[mm²]　
Wt＝1000 であるとすれば、引張応力σは、σ=1000/78.5=12.7[N/mm²] 　
円柱断面直径dが d=5[mm] であるとすれば、断面積 A=πd²/4=19.6[mm²]　
Wt＝1000 であるとすれば、引張応力σは、σ=1000/19.6=50.9[N/mm²]　

つまり同一荷重に対して、部材直径が1/2になると引張応力は4倍になります。
引張応力が高すぎると部材が耐え切れずに破断する場合があります。

（2）圧縮応力とは

図2のような断面積A[mm²]の円柱の両端から、円柱を軸方向に押し付ける荷重Wc[N]が加わっているとします。このような荷重を「圧縮荷重」、圧縮荷重を受ける部材に発生する応力を「圧縮応力」（compressive stress）といいます。
圧縮応力も部材の断面に対して垂直に作用する垂直応力です。
記号は引張応力と同じσを用いますが、負記号（マイナス）をつけて引張応力と区別します。

圧縮応力の求め方

圧縮荷重 Wc=1000[N]、円柱断面直径dが d=10[mm] であるとすれば、
断面積 A=πd²/4=78.5[mm²] であることから
圧縮応力は σ=-1000/78.5=-12.7[N/mm²] となります。

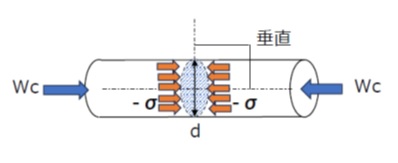
【図2　圧縮荷重と圧縮応力】

圧縮荷重を受ける長柱形状の部材の場合、「座屈」が問題になることがあります。

［※関連記事：長柱と座屈（bucking） はこちら］

（3）せん断応力とは

部材を切断しようとする方向（部材の軸線に対して横方向）に作用する荷重を「せん断荷重」、せん断荷重を受ける部材に発生する応力を「せん断応力」（shear stress）といいます。

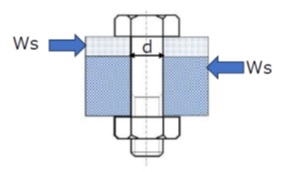
【図3　せん断荷重とせん断応力】

せん断応力の求め方

例として、図3のようなリーマボルトで締結された2枚の板の断面方向、すなわちリーマボルトの軸線に対して横直角方向の荷重W_sが加わったとします。
W_sをリーマボルトの断面積で割った値が「せん断応力」となります。
せん断応力を表す記号としてギリシャ文字のτ（タウ）を用います。

リーマボルトの直径をd[mm]、せん断荷重をW_s[N]とすれば

　せん断応力 τ=Ws/(πd²/4) [N/mm²]

せん断応力は、回転機械の主軸のようにトルクを受けてねじられる方向の力が作用する部材にも発生する応力です。

（4）曲げ応力とは

回転機械の主軸のような細長い形状の部材（はり）の両端に大きさが等しく方向が相反する力（偶力）が作用すると、はりは曲がろうとします。この偶力のことを「曲げモーメント」（bending moment）、曲げモーメントにより部材に発生する応力を「曲げ応力」（bending stress）といいます。
曲げモーメント（偶力）は物体を回転させようとする作用を行うので、その単位は力のモーメントと同じ[N・mm]となります。

はりに曲げモーメントが加わると、図のようにはり部材断面の中心には曲げ応力がゼロになる中立点が存在する一方で、中立点から離れた部材の凸側には引張応力、凹側には圧縮応力が発生し、その値は部材の表面において最大となります。

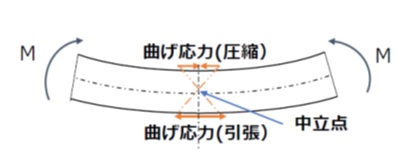
【図4　曲げモーメントと曲げ応力】

曲げ応力の求め方

曲げ応力を表す記号にはσbを用い、その最大値をσb_maxと表すことにします。
σb_max　は曲げモーメントMを、部材の断面係数z[mm³]で割った値です。

　σb_max = M/z　[N/mm²]

断面係数は、材質には関係なく部材の断面形状のみによって決まる値で、曲げ荷重を受ける機械の構造強度設計上、重要な係数です。

［※関連記事：「はり」の基礎知識を習得！SFDとBMD、たわみの計算方法は？ はこちら］

（5）ねじり荷重とせん断応力について

ポンプ、圧縮機などの回転機械の主軸はトルクTを与えられて回転します。このとき軸はトルクTによって、ねじられた状態となります。

トルクT[N-m]、主軸（丸棒）の直径をd[mm]、トルクによるねじりで軸の断面に生ずるせん断応力をτとすると、次の関係があります。

　τ=16T×1000/(πd³) [N/mm²]

また軸に作用する動力をP[kW]、軸の回転速度をn[min^-1]とすれば
　T=60×1000×P/(2πn)　 [N-m]
となります。

３．荷重と応力の関係を整理

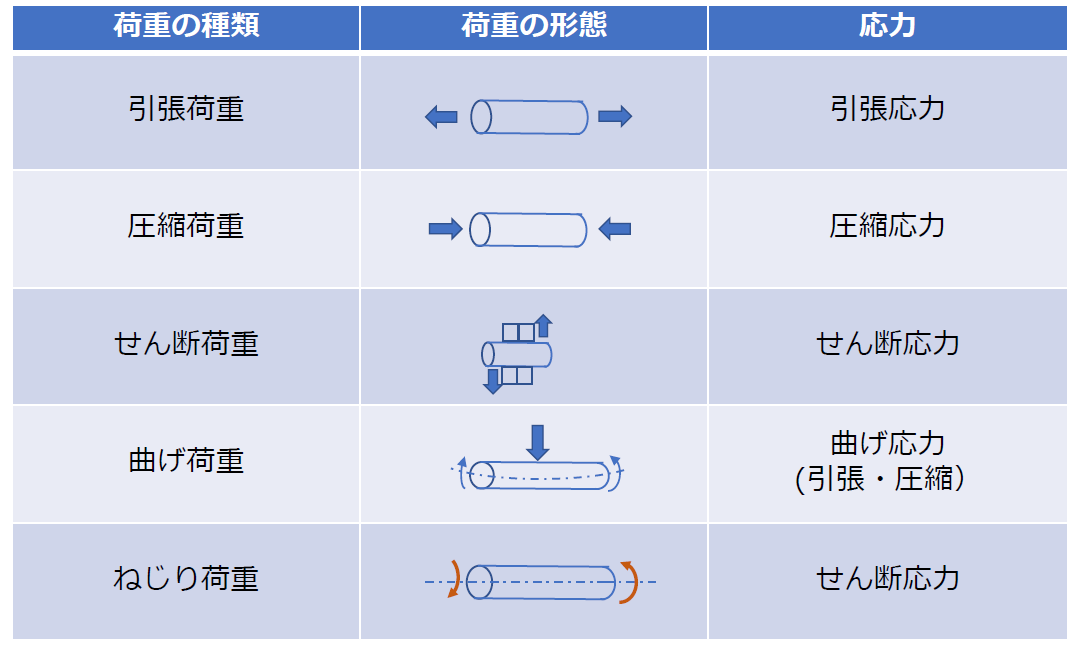
以上、今回取り上げた5種類の荷重と応力の関係をまとめると表1のようになります。

【表1　荷重と応力の種類】
（※当連載の「荷重、応力、ひずみ」の回で掲載した表です）

ということで今回は、機械に作用する荷重に対してどのような種類の応力が生じるのかについて、基本的な事項を解説しました。
機械を適切に設計するためには、応力に関連してさらに様々な用語を理解し、設計に活かしていくことが重要です。先ずは本コラムで解説した内容について理解した上で、次の段階へ進むようにしましょう。
 
 
（アイアール技術者教育研究所　S・Y）
 

Tweet

Pocket