長柱の座屈を解説!オイラーの公式、座屈荷重・座屈応力の求め方がわかる

1.座屈とは?
主に圧縮荷重を受ける真直な棒を「柱」といいます。
柱が短い場合は、圧縮荷重に対して真直に縮み(圧縮ひずみの発生)、圧縮応力が材料の圧縮強さに達すると破壊(変形)が起きます。
柱が断面寸法に比して長い場合は、軸荷重がある値に達すると、応力は材料の圧縮強さに比較して低くても、それまで真直に縮んでいた柱が急に側方にたわみ始め大きく変形して破壊します。このように細長い柱が圧縮力を受けるとき、応力自体は低くとも、不安定な変形が生じる現象を「座屈」(buckling)といいます。
また、座屈が起きるときの圧縮荷重を「座屈荷重」といいます。
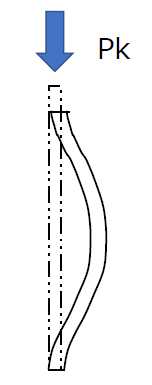
【図1 長柱の座屈】
強度の高い材料を使って、ベースやフレームなど圧縮荷重を受ける機械用構造物の縦方向の部材断面積を小さく設計しようとする場合などには、座屈に注意することが求められます。
2.座屈とオイラーの公式
座屈荷重をPk, 部材の断面二次モーメントをI、柱の長さをL、とすると
Pk=nπ2EI/L2 ・・・(1)
(1)式を、座屈に関するオイラーの公式といいます。
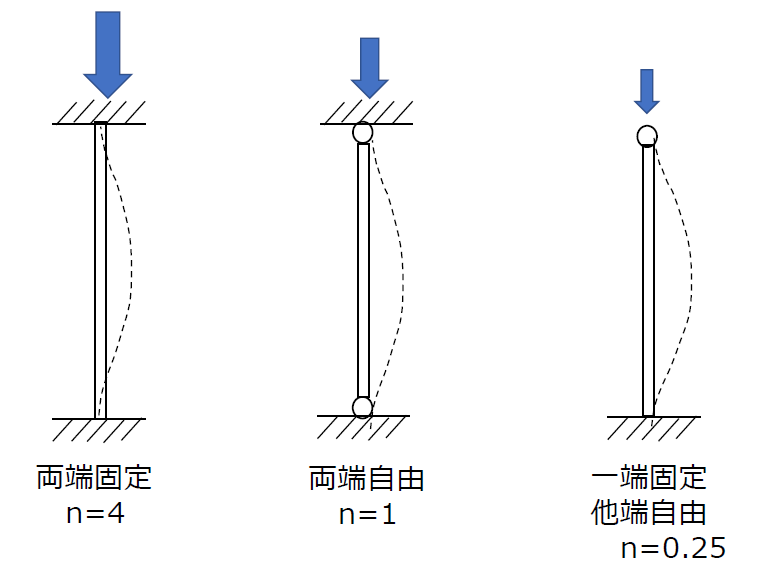
ここでnは、柱両端の支持形状によって定まる係数で、
両端固定の場合 n=4
両端自由(回転端)の場合 n=1
一端固定、他端自由の場合 n=0.25
となります。
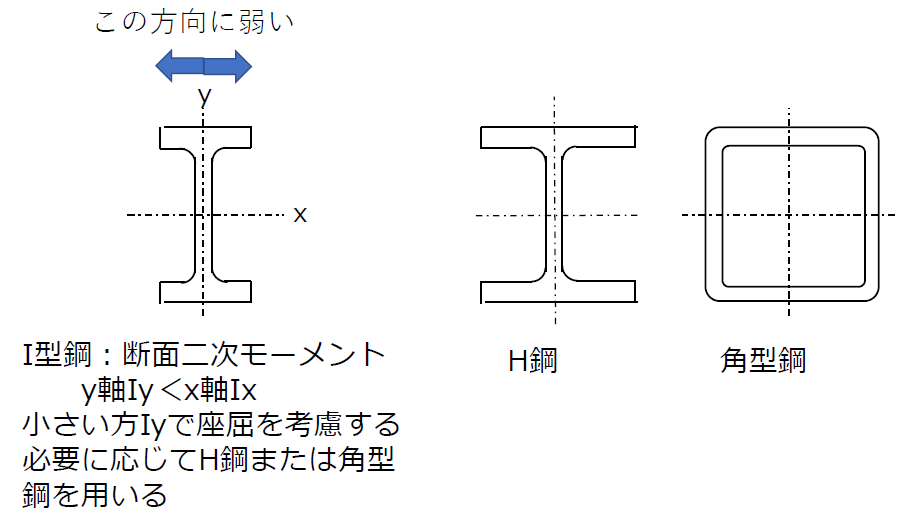
座屈は部材断面の最も弱い方向へ起きるので、評価する際、断面二次モーメントはその値が最も小さくなる方向の軸に関する値を用います。
I形鋼の場合は図のy軸に関する断面二次モーメントが小さくなります。必要に応じてH鋼または角型断面鋼を用いることで、断面二次モーメントの均一化を図ることができます。
[※関連記事:断面二次モーメントを徹底解説!基本概念から求め方・計算例までわかりやすく説明 ]
座屈応力と細長比
柱の断面積をAとしたとき、
k=√(I/A) ・・・(2)
kを「断面二次半径」といい、
L/k ・・・(3)
を「細長比」といいます。
座屈荷重に対して発生する座屈応力σcは(1),(2),(3)式より
σc=Pk/A=nπ2EI/L2A=nπ2E/(L/k)2 ・・・(4)
オイラーの公式は、柱が短くて座屈が起きる前に圧縮強さが支配的となる場合は適用できません。
材料の圧縮降伏点応力の値を(4)式の左辺に代入することで、オイラーの公式を適用できる細長比を知ることができます。細長比が小さくなっていくと(4)式で計算されるσcが大きくなりますが、この値が材料の圧縮降伏点応力σsより大きくなれば、座屈する以前に圧縮応力による変形が生じるためです。
3.オイラーの公式が適用できない中間柱での危険応力の求め方
圧縮荷重を受ける柱の強度は、短柱の場合は圧縮強さが、長柱の場合は座屈が問題となります。
オイラーの公式が適用できない中間長さの柱では、その両方を考慮する必要があります。実用的にはオイラーの公式が適用できない範囲の中間柱となることが数多くあり、実用的な見地から材料の圧縮強さと座屈応力の両方を考慮した幾つかの公式が提案されています。
ジョンソンの公式
オイラーの公式が適用できない範囲で、比較的有効に危険応力を見積もることができると考えられているのがジョンソンの公式です。
危険応力(中間柱における座屈応力)をσc、材料の圧縮降伏点応力σsとすればジョンソンの公式は次のようになります。
σc=σs-(L/k)2σs2/4nπ2E ・・・(5)
中間柱に関する公式には、紙面の関係で省略しますが、他にランキンの公式と、テトマイヤーの公式があります。両者とも、材料によって決まる実験定数を用いて危険応力を計算する公式です。
(4)式(5)式より、細長比を小さくするほど座屈応力もしくは危険応力は大きくなる、すなわち圧縮荷重に対する耐性が大きくなるので、柱が変形しにくくなることがわかります。
(2)式(3)式より、断面二次モーメントを大きくするほど断面二次半径kが大きくなるため、同じ柱長さLに対する細長比が小さくなります。
つまり、柱を強くするためには、なるべく断面二次モーメントが大きくなるような形状を選ぶと良いことがわかります。
柱の圧縮荷重に対する強度確認の方法
しかし、細長比を小さくすることでオイラーの公式が適用できなくなる可能性があるので、次の手順で柱の圧縮荷重に対する強度を確認します。
圧縮荷重を受ける構造部材(柱)を設計するとき、柱上下端の拘束条件からnを求め、材料特性から圧縮降伏点応力とヤング率とともに(4)式に代入して限界細長比を逆算します。この値が、柱の長さ、断面積と断面二次モーメントから計算される設計形状における細長比の値を下回っていれば、形状は長柱であってオイラーの公式の適用範囲となり、設計形状における細長比を(4)式に代入して設計条件における座屈応力を求め、(1)式から座屈荷重を求めることができます。
実際の荷重が座屈荷重を上回る場合は、断面形状の工夫により断面二次モーメントを高めて、耐荷重を向上させます。
しかし、断面二次モーメントを大きくすることでオイラーの公式の適用範囲外となる可能性があります。
(4)式から逆算した限界細長比が、断面二次モーメント向上により小さくなった設計形状における細長比の値を上回るときは、オイラーの公式が適用できない中間柱となります。そのため、ジョンソンの公式(5)を用いて、危険応力を計算し、実際の圧縮荷重に対して発生する圧縮応力(荷重/断面積)が危険応力(中間柱における座屈応力)を下回っていることを確認するのが実用的と考えられます。
(日本アイアール株式会社 特許調査部 S・Y)