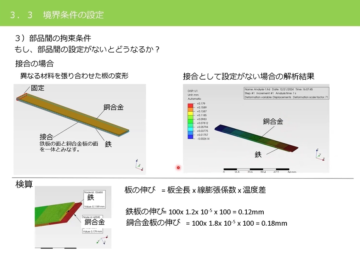
【機械設計マスターへの道】「はり」の基礎知識を習得！SFDとBMD、たわみの計算方法は？

Tweet

Pocket

機械を設計する際に、軸などの機械部品を建物の水平部材に使用する「はり」（梁）として考え、はりに加わる荷重とはりの支持条件に対して、はりに発生する応力や変形（たわみ）を計算することがあります。

このコラムでは、機械設計者として知っておくべき材料力学におけるはりの基本知識について解説します。

１．はりの支持状態

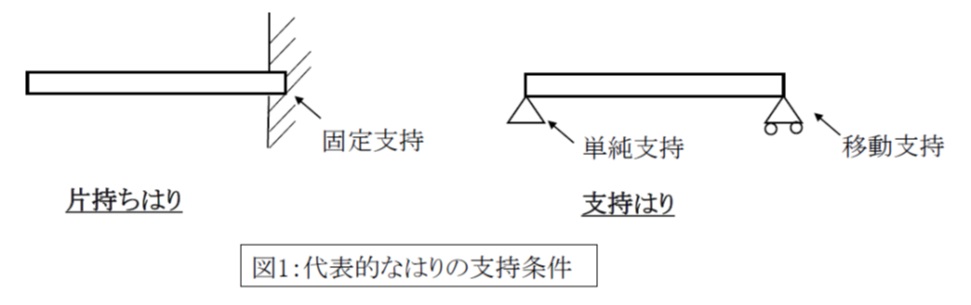
はりの支持状態として、「固定支持」「単純支持」「移動支持」の3種類があります。

• 固定支持は、上下、左右、回転すべての動きを拘束します。
• 単純支持は、上下、左右の動きは拘束しますが、回転は拘束しません。
• 移動支持は、上下の動きのみを拘束し、左右の動きと回転を拘束しません。

機械設計に必要となる支持条件として多く出てくるのが、図1左のような片側固定支持、反対側が自由端の「片持ちはり」と、図1右のような片側単純支持、反対側移動支持の「支持はり」です。

２．はりに働く力と静定はり

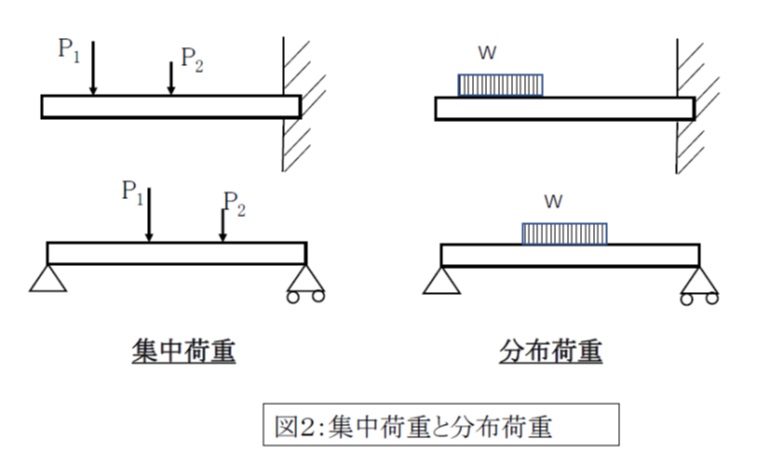
図2のように、はりの1点に作用する「集中荷重」と、ある範囲にわたって単位長さあたりwの荷重が作用する「分布荷重」とがあります。

荷重に対して、はりの支点には反力が発生します。
荷重の大きさとその位置が与えられたときに、静力学的なつり合い条件だけから反力を求めることができる場合を「静定はり」、求めることができない場合を「不静定はり」といいます。

本コラムでは「静定はり」について考えることにします。

３．SFDとBMD

荷重と支点反力は、はりにたいして垂直方向にせん断力として作用します。

また、荷重とはりの支持方式に応じて、はりには曲げモーメントが加わります。
［※曲げモーメントについては、本連載の「荷重、応力、ひずみ」のページをご参照ください。］

上方向を＋、下方向を―として、はりに加わるせん断力の大きさを示した図をSFD（Shear Force Diagram）といいます。
また、はりの両端を上に曲げるような方向を+として、はりに加わる曲げモーメントの大きさを示した図をBMD（Bending Moment Diagram）といいます。

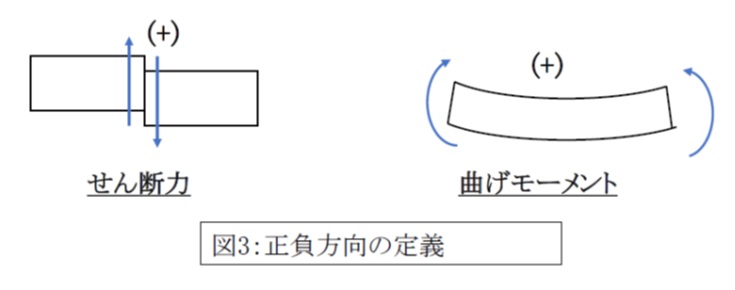
図3のように、せん断力は、はりの左の部分に対して右の部分を押し下げる方向を正、反対向きを負とします。
曲げモーメントは、はりを上向きに曲げるように作用する場合を正、反対向きを負とします。

SFDとBMDの導出について簡単な例で解説します。
 

（1）集中荷重を受ける支持はり

図4のように、支点間距離（スパン）ℓの支持はりの支点Aから距離aにある断面に1個の集中荷重Pを受ける場合を考えてみます。

Aに生じる反力をR₁,Bに生じる反力をR₂とすれば、支点Aまわりの力のモーメントのつり合いからR₂ℓ－Pa=0
したがって、R₂=Pa/ℓ
同様に支点Bまわりの力のモーメントのつりあいから、R₁=Pb/ℓ
支点Aから荷重点までの間では、せん断力F= R₁=Pb/ℓ
荷重点から支点Bまでの間では、F= R₁-P=- R₂=-Pa/ℓ
となって、荷重点を境に正負が入れ替わります。

荷重点より左側の任意断面に作用する曲げモーメントは
　Mx= R₁x=Pbx/ℓ
荷重点より右側の任意断面に作用する曲げモーメントは
　Mx= R₁x-P(x-a)=a(ℓ-x)P/ℓ
となります。

曲げモーメントは両支点において0、荷重点（x=a）において最大値Pab/ℓとなり、BMDは、荷重点における最大値へ向かう直線になります。

 

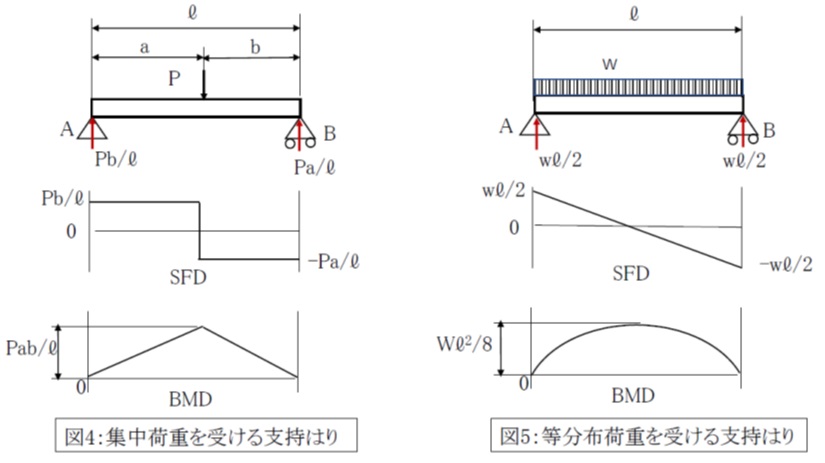
（2）等分布荷重を受ける支持はり

図5のようにはりの全長にわたって等分布荷重wを受けるスパンℓの支持はりを考えます。

全荷重wℓを両方の支点で等分に支えるので支点反力は
　R₁= R₂=wℓ/2
支点Aから距離xの任意断面におけるせん断力Fxは
　Fx= R₁-wx=wℓ/2-wx
となって、SFDは支点Aにおけるwℓ/2から支点Bにおける- wℓ/2まで直線に変化する形になります。
支点Aから距離xの任意断面における曲げモーメントMxは、
　Mx= R₁x-wx・x/2=wx(ℓ-x)/2
となります。

したがって、BMDは二次式で表される放物線となり、両支点において0、はりの中央部で最大値wℓ²/8 となります。
 

（3）自由端に集中荷重を受ける片持ちはり

図6のように、自由端に集中荷重Pを受ける片持ちはりを考えます。

せん断力は負の値をとり、その値はF=-P一定となります。
曲げモーメントも負の値を取り、自由端からの距離xに対してMx=-Pxとなります。
BMDは自由端で0、固定端で最大値-Pℓをとる直線となります。

 

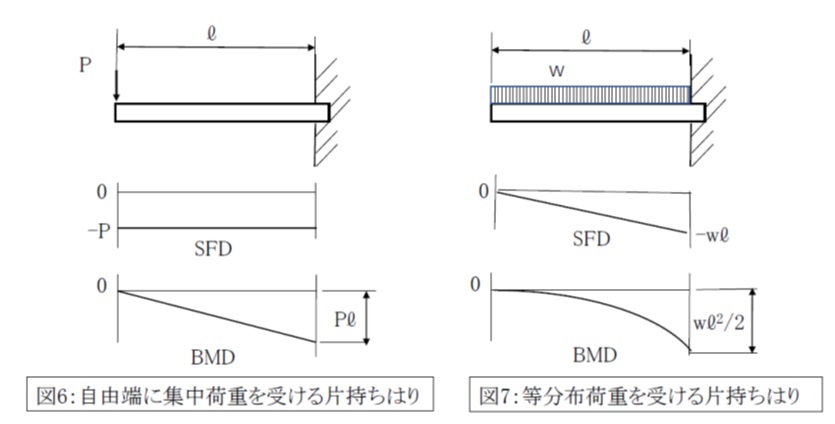
（4）等分布荷重を受ける片持ちはり

図7のように、はりの全長にわたって等分布荷重wを受ける片持ちはりを考えます。

自由端から任意の距離xの断面におけるせん断力は、Fx=－wxとなります。
曲げモーメントは、等分布荷重wxの重心位置がx/2にあることからMx=-wx²/2となり、BMDは自由端で0、固定端（x=ℓ）で最大値-wℓ²/2をとる二次曲線になります。
 

４．曲げ応力と断面係数

最大曲げ応力σ_bmaxは、曲げモーメントMを部材断面形状から求まる断面係数Zで割ることで計算することができます。
［※詳細は、本連載の「荷重、応力、ひずみ」の回（曲げ応力の解説）をご参照ください。］

　最大曲げ応力σ_bmax=M/Z

曲げモーメントの方向を見極め、断面係数Zが大きくなるような断面形状を選ぶことにより、部材を経済的に使用しつつ、曲げモーメントに対して発生する曲げ応力の大きさを低減することができます。
 

５．はりのたわみと断面二次モーメント

上述のように、断面係数Zは、曲げモーメントMとはりに生じる最大曲げ応力の関係を示す定数です。
一方、断面二次モーメントIは、曲げモーメントMと、曲げモーメントを受けてたわむ（変形する）はりの曲率の関係を示す定数です。
いずれも曲げモーメントを受けるはりの強さ、剛性を表す指標ということができます。

はりの任意の断面に作用する曲げモーメントをMx、はりの中立軸に関する断面二次モーメントをI、 曲げモーメントを受けてたわむはりの曲率半径をR、部材の縦弾性係数（ヤング率）をEとすれば、次の関係があります。

　1/R=Mx/EI　　・・・(1)

（1）式からEIが大きいほどRが大きい（曲率が小さい）、すなわちたわみ量は少ない（変形が小さい）ということになります。
EIは、はりの曲がりにくさを示す指標であり、「曲げ剛性」（曲げこわさ）といいます。

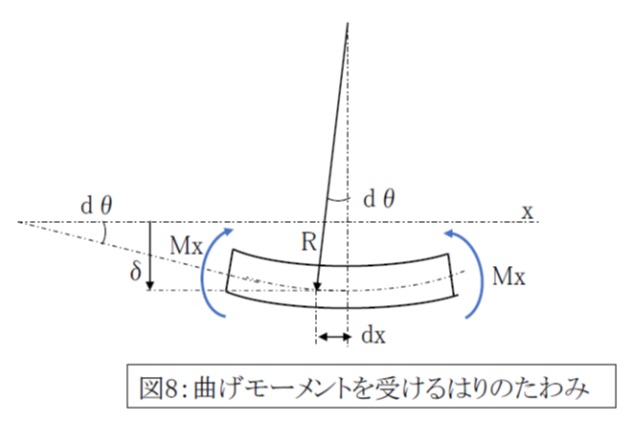
図8のように、たわみδが0である中立軸線xに対して、たわみ曲線への切線がなす角度をdθとします。
dθは小さい値ですからtan(dθ)≒dθとおくことができます。

図8の幾何学的関係より、
　R tan(dθ)≒Rdθ=dx　　・・・ (2)
また、　
　tan(dθ)≒dθ=dδ/dx　　・・・(3)
(1),(2),(3)式より　
　d²δ/dx²=Mx/EI　　　・・・(4)
となります。

したがって、はり全長方向の任意の位置xにおけるはりのたわみδxは、BMDで表される曲げモーメントMxを（4）式に代入して、はりの始点からxまで2重積分することにより求めることができます。

代表的な支持条件と荷重条件に対する最大たわみδmaxは、次のような値となります。
（導出過程は省略します。）

• 自由端に集中荷重Pを受ける片持ちはり（はり全長ℓ）：
  　最大たわみは、自由端に生じ、δmax=Pℓ³/3EI
• 等分布荷重wを受ける片持ちはり（はり全長ℓ）：
  　最大たわみは、自由端に生じ、δmax=Pℓ⁴/8EI
• 支点間の中央に集中荷重Pを受ける支持はり（支点間距離ℓ）：
  　最大たわみはスパンの中央の荷重点に生じ、δmax=Pℓ³/48EI

同じ値の集中荷重が、片持ちはりの先端に作用する場合と、支持はりの中央に作用する場合とでは、最大たわみ量に16倍もの違いが生じます。
 

他にも様々な支持条件、荷重条件に対する、SFD、BMD、たわみ角、たわみ量、の計算公式は、機械工学便覧や材料力学教科書から知ることができますが、考え方の基本的な理論は理解しておくことが重要です。

（日本アイアール株式会社　特許調査部　S・Y)
 

Tweet

Pocket