焼きばめ・冷やしばめに関する必須知識と計算方法を解説!しめしろの考え方、面圧やトルクの計算例など

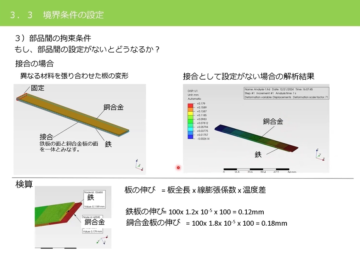
今回は、温度差による寸法変化(膨張・収縮)を利用して円筒形状の部品を軸部品にはめて、強固な固定状態を実現する「焼きばめ(焼き嵌め)」「冷やしばめ(冷やし嵌め)」について、考えてみることにします
1.しまりばめ
穴と軸を組み合わせて使用する機械部品は数多く存在します。
焼きばめ(焼き嵌め)・冷やしばめ(冷やし嵌め)を適用するのは、穴径が軸径よりも小さい「しまりばめ」の場合です。
これを組み立てるために穴部品を熱して穴径を広げる(焼きばめ)、あるいは軸部品を冷やして軸径を縮める(冷やしばめ)必要があります。
軸径と穴径の差は、「しめしろ」といいます。
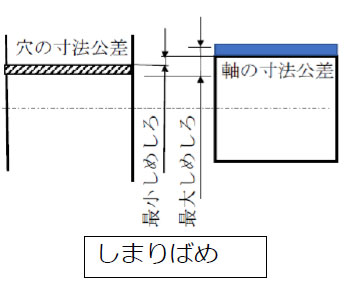
【図1 しめしろ】
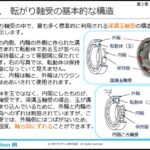
軸受(ベアリング)の内輪と軸、軸受のハウジングと軸受外輪、軸継手と軸、車輪と軸、スリーブ部品と軸など、分解頻度があまり高くない回転部品では、穴側の部品を焼きばめ により軸部品に取り付けることが多くあります。
2.線膨張係数としめしろ
鉄鋼材料の線膨張係数は、11.8×10-6/K です。
例えば、穴径が50H7、軸径が50s6であるとします。
穴径の公差は50.025~50.000(H7)、軸径の公差は50.059~50.043(s6)です。
最大しめしろは 50.059-50.000=0.059、最小しめしろは 50.043-50.025=0.018 となります。
穴部品を軸に嵌めるために、内径を50.059よりも大きく広げる必要があります。
穴径が公差下限の50.000に製作されたとして、
温度差100Kで、内径は 50x(1+11.8 x10-6x100)=50.059 となり軸径の最大値とちょうど等しくなり、
温度差200Kで、50x(1+11.8 x10-6x200)=50.118 になって軸径より大きくなります。
温度を上げるほど径が広くなるので取付けは容易になりますが、あまり温度を上げ過ぎると、材料の熱処理温度域にかかる可能性があるので注意が必要です。
また、穴が均一に広がらないとうまく入らずにかじりつく恐れもあるので、焼きばめを行う際は、温度だけではなく部品全体を均一に熱するように管理する必要があります。
冷やしばめ の場合は、ドライアイスなどを利用して軸部品を冷やして収縮させますが、そのときの温度は-70℃程度であって、常温を20℃とすれば90K程度の温度差が限界となります。
したがって、あまり大きなしめしろ には適用できません。ブッシュなどの部品を穴にはめるような場合に適用します。
3.焼きばめ応力と面圧
焼きばめで取り付けた穴部品は、冷えて常温に戻ると収縮しようとしますが、軸に阻まれて元の寸法へ戻ることはできません。
その結果、穴の内面と軸の外面には、「面圧」という接触圧力が生じて、円筒部品は軸に対して強固に固定されます。
面圧の計算例
導出過程は省略しますが、円筒材料のヤング率をE[Mpa]、円筒の外径をDo[mm]、内径をDi[mm]、しめしろをδ[mm]とすれば、この円筒を中実軸に焼きばめしたときの面圧pは、次式で計算することができます。
p=Eδ(Do2-Di2)/(2DiDo2) [MPa]
一例として、E=210×103[MPa] (鉄鋼材料)、δ=0.1[mm]、Do=150[mm]、Di=100[mm]のとき、(δ/Di=1/1000)
p=210 x103x0.1x(1502-1002)/(2x100x1502)=58.3[MPa]
となります。
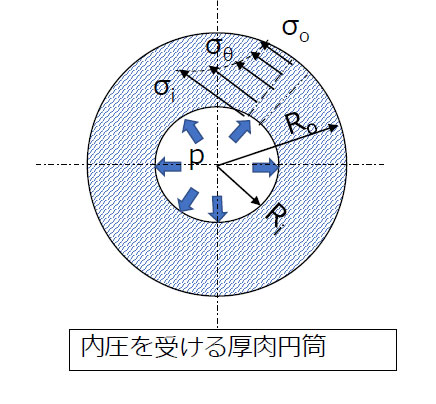
【図2 円筒を中実軸に焼きばめしたときの面圧】
このとき円筒は内圧pを受けるのと同じ状態となり、周方向に引張応力が発生します。
焼きばめの場合は、薄肉円筒ではなく、肉厚が外径の0.25倍よりも大きい厚肉円筒となることが多く、内面から外面に至る間の周方向応力の変化を考慮する必要があります。
[※薄肉円筒については、薄肉円筒胴と薄肉球形胴の強度計算(必要肉厚)のページをご参照下さい。]
周方向応力の計算例
厚肉円筒において円筒外面半径をRo[mm]、内面半径をRi[mm]とすれば、半径rの位置における周方向応力σrtは、次式で計算することができます。
σrt=pRi2(1+Ro2/r2)/(Ro2-Ri2) [MPa]
応力は内面(r=Ri)で最大、外面(r=Ro)で最小となります。
内面に生じる周方向の応力をσθi、外面に生じる周方向の応力をσθo とおくと、上記の例の場合、次のような値になります。
σθi=58.3×502(1+752/502)/(752-502) =152[MPa] (最大値)
σθo=58.3×502 (1+752/752)/ (752-502)=93.3[MPa] (最小値)
焼きばめ応力が、材料の強度上問題ない値であるかを確認する必要があります。
4.トルク伝達
しめしろを大きくすれば、面圧も大きくなります。
接触面にはたらく面圧による力が大きければ、静止摩擦力により回転トルクを伝達することも可能です。
トルクを伝達する軸継手は、キーを用いて軸にトルクを伝達することが通常です。
[※キーについては、機械要素「キー」と「キー溝」の製図を学ぶ!のページをご参照下さい。]
キーを使用せずに軸継手を取り付けることができれば、キー溝による応力集中の影響を排除することができ、キー隙間によるアンバランス要因がなくなるので、回転体のつり合い良さを高めるうえでも有利です。
トルク計算の例
上記の例(Di=100mm)で、長さL=80[mm]のハブの軸継手でトルク伝達を行うとします。
ハブ内面の接触面積Aは、A=πDiL=25132[mm2]であり、
ハブと軸の接触面における静止摩擦係数を μ=0.15 とすれば、
接触面で伝達可能なトルクTtは、
Tt=摩擦係数x面圧x接触面積x半径
=μpADi/2=0.15x58.3[N/mm2]x25132[mm2]x0.1[m]/2=10988[N-m]
となります。
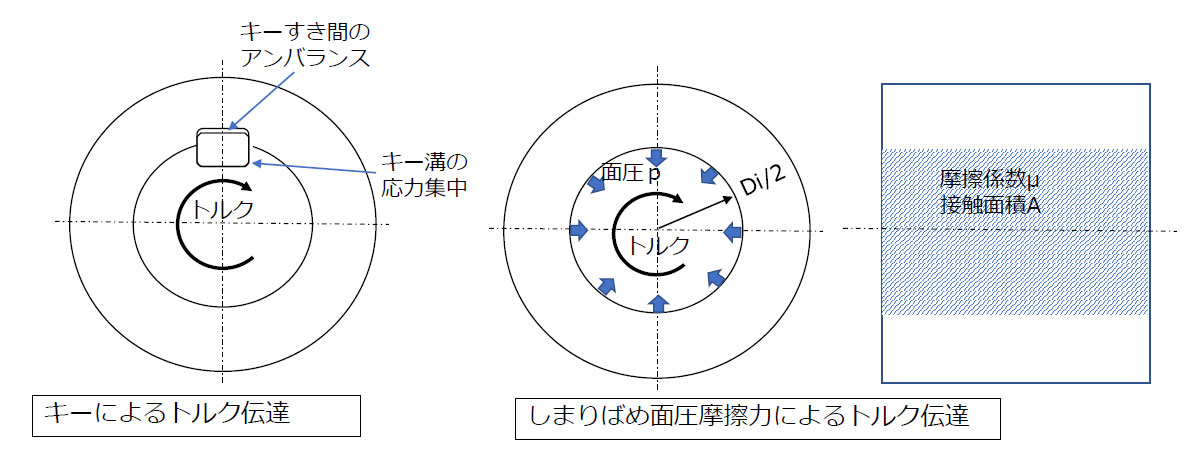
【図3 しまりばめとトルク伝達】
一例として、軸動力P=2000[kW]、回転速度n=3580[min-1]であるとすれば、負荷トルクTpは
Tp= T=60x1000xP/(2πn)=5335[N-m]
となって、伝達可能トルクTtは負荷トルクTpよりも十分大きく、トルクを伝達することが可能ということになります。
ただし、負荷トルクの変動や衝撃トルクの発生がある場合は、Tpに対してさらに大きなトルク余裕を見込む必要があります。
5.油圧ばめ(ハイドロフィット)
キー無しでトルク伝達を行う場合、通常は上記例のように、焼きばめしろδと軸径(ハブ内径)の比 δ/Di を 1/1000程度にとります。
このように大きなしめしろの場合は、焼きばめするのに必要な温度差が大きくなります。また、現場で適切な焼きばめ設備(炉など)が無い場合もあります。
そこで、焼きばめに替わって、油圧によりハブ内径を広げて軸に装着する方法があります。
図のように軸端をテーパとして、ハブの内径両側にOリングを装着してシールして、ハブと軸の装着面に油圧(しめしろにより発生する面圧を超える値)をかけてハブ内径を広げ、テーパに沿って前進させて、規定のしめしろを得ることができます。
例えば、テーパが1/10、軸径が100であれば、1㎜押し込んだ状態で、しめしろ0.1となります。
軸端にはねじ部を設けて、ハブ挿入後、軸端ナットで押えます。
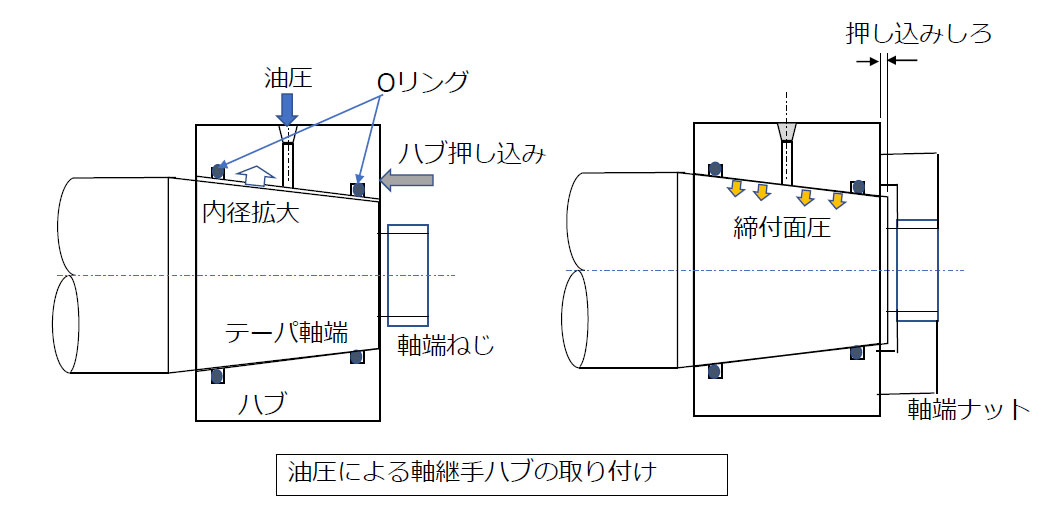
【図4 油圧ばめとしめしろ】
軸端ねじのピッチが2であれば、ナットをハブ端面に押し当てた状態から半回転させると、ハブは軸方向に1㎜進んで、規定のしめしろが得られることになります。
トルク伝達に必要なしめしろが確保されて、かつ過大面圧によるハブや軸の降伏強度の問題が発生しないように、適正に押し込み量を管理することが重要です。
(アイアール技術者教育研究所 S・Y)