【機械設計マスターへの道】薄肉円筒胴と薄肉球形胴の強度計算（必要肉厚）

Tweet

Pocket

今回は、ガスや液体を貯留し内面に大気圧より高い圧力を受ける圧力容器について、薄肉円筒胴と薄肉球形胴の強度（必要最小肉厚）について考えてみます。

１．薄肉円筒胴

円筒胴の内径をDi、胴の厚さをtとするとき、t/Di≦0.25 の場合を薄肉円筒と定義することが一般的です。

ここでは、3次元応力を円柱座標（半径方向r,周方向θ,軸方向z）で定義します。
内部に作用する圧力をpとします。

胴の周方向に生じる円周応力をσ_θで表します。円周応力σ_θのことを膜応力（フープ応力）とも呼びます。
円筒胴の半径方向（厚さ方向）に生ずる半径応力をσr、長手方向に生ずる応力を軸応力σzと表します。

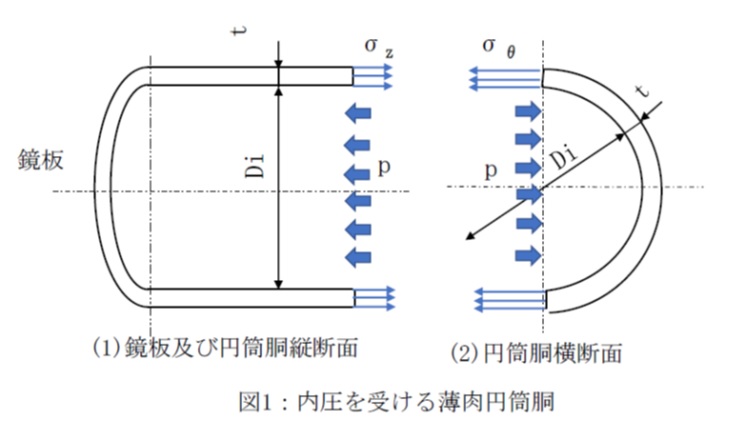
図1（1）円筒縦断面図に示すように、軸応力σzは一定の大きさで厚さ方向に分布します。
t<< Diであることから、軸応力の作用面積は近似的にπDitとすることができます。
圧力pが作用する円筒の断面積はπDi2/4ですから
　σz=pπDi²/4/πDit= pDi /4t　　・・・（1）
となります。

円周応力σ_θについては、図1（2）円筒胴横断面図に示すように、薄肉の場合は近似的に厚さ方向に沿って一様に分布すると考えることができます。
横断面の軸方向に単位長さの厚さをとれば、円周応力σ_θが作用する面積は2tx1=2tとなります。
また内圧pが作用する単位長さ当たり投影面積はDix1＝Diとなります。

したがって、次のようになります。
　σ_θ=p Di /2t　　・・・（2）

（1）、（2）式よりσz=σ_θ/2　、すなわち軸応力は円周応力の2分の1となります。
半径応力σrは、内面で-p(圧縮)から外面で0まで単調に変化し、薄肉円筒の場合、σr≒0として扱うことができます。

以上より、薄肉円筒の強度（必要最小肉厚）を考えるとき、円周応力（膜応力）σ_θが支配的となります。
実用上必要な肉厚を計算する際には、次式によりσθを補正します。

　σ_θ=p (Di＋2βt)/2t　　・・・(3)

高圧ガス規格などでは、β=0.6としており
　σ_θ=p (Di＋1.2t)/2t　　・・・(4)
となります。
 

強度設計における「溶接継手効率」の考慮

薄肉円筒は、薄板を円筒状に巻いて端面を溶接で接合して作ることが多いので、強度計算に当たっては溶接継手効率（母材および溶着金属の機械的性質、溶接性、溶接方法、継手の種類・形状、溶接後の熱処理、検査方法、荷重状態、使用条件などを考慮して決める、母材の許容応力に対する比率）を考慮する必要があります。

溶接継手効率をη（イータ）、母材の許容引張応力をσa[MPa]とすれば、(4)式より設計応力としての σ_θ [MPa]の上限値は、
　σ_θmax=σaη=p(Di＋1.2t)/2t　　・・・(5)
(5)式より、薄肉円筒胴の必要肉厚tn[mm] は
　tn= p Di /(2σaη-1.2p)　　・・・(6)
となります。

一例として、p=5[MPa], Di=500[mm], σa=100[MPa] のとき、η=0.8 であるとすれば
tn=5×500/(2x100x0.8-1.2×5)=16.3[mm] となります。
設計板厚を20に取った場合、t/Di=0.04 となります。(t<<Di)

なお、円筒胴には図1（1）の左側部分のように両端に閉じるための「鏡板」を設ける場合が多くあります。
鏡板は内圧を受ける蓋であり、その形状ごとに必要肉厚を計算する式がありますが、本コラムでは省略します。

２．薄肉球形胴

球形胴の内径をDi、胴の厚さをtとするとき、一般的に t/Di≦0.178 の場合を薄肉球形と定義することが多いようです。球形胴の中心を通る断面は、図1（2）に示す円筒胴横断面と同じになります。

しかし、円筒胴の場合は断面が紙面垂直方向（軸方向）に半円筒となるのに対して、球形胴の場合は紙面垂直方向に半球形となります。
このとき球形胴の円周方向（接線方向）に生じる接線応力σ_θが作用する形状は、内径Di 、厚さtの薄肉円輪であり、その面積は t<<Di であることから πDi t です。
また内圧pの投影作用面積は、直径Diの円に相当する πDi²/4 となります。

したがって、接線応力σθは、
　σθ=pπDi²/4/πDi t= pDi/4 t
となって、（1）式の薄肉円筒の軸応力σzと同じ値で、（2）式の薄肉円筒のときの円周応力の2分の1の大きさとなります。

すなわち、補正を考えない場合、薄肉球形胴は同じ圧力、同じ内径に対する必要肉厚を薄肉円筒胴の2分の1にすることができます。
ガスタンクやLNG船のタンクが球形になっているのはこのためです。

球形胴は中心点に対して完全な対称ですから、中心を通る任意断面に対して、同じ接線応力σ_θが生じることになります。円筒胴と同様に球形胴の場合も、半径応力σrは内面で-p(圧縮)から外面で0まで単調に変化し、σr≒0として扱うことができます。
薄肉円筒と同様、実用上必要肉厚を計算する際は、（7）式でσ_θ補正を行います。

　σ_θ=p (Di＋2βt)/4t　　・・・(7)

高圧ガス規格などでは、薄肉球形胴ではβ=0.2としており、
　σ_θ=p (Di＋0.4t)/4t　　・・・(8)
となります。

溶接継手効率をη、母材の許容引張応力をσa[MPa]とすれば　（8）式より設計応力としての σ_θ[MPa] の上限値は
　σ_θmax=σaη=p(Di＋0.4t)/4t　　・・・(9)
となり、(8)式より、薄肉球形胴の必要肉厚tn[mm] は次のようになります。
　tn= p Di /(4σaη-0.4p)　　・・・(10)

一例として、p=5[MPa], Di=500[mm], σa=100[MPa] のとき、η=0.8であるとすれば
tn=5×500/(4x100x0.8-0.4×5)=7.9[mm] となります。
設計板厚を10に取った場合、t/Di=0.02 となります。(t<<Di)

なお、薄肉円筒胴、球形胴ともに板取りの際には(6),(10)式で計算される厚さに、所定のくされしろや、公差、加工による減肉を加味して手配する板厚を決定します。
 

（日本アイアール　特許調査部　S・Y）
 

Tweet

Pocket