位置公差は部品の位置を規制する幾何公差|位置度/同軸度,同心度/対称度の使い方

前回の幾何公差の解説では、部品の角度を規制する「姿勢公差」をご説明しました。
今回は、部品の位置を規制する「位置公差」について解説します。
目次
1.位置公差(位置偏差)とは
形状公差や姿勢公差は、形や角度を規制するものでしたが、位置に関しては規制しませんでした。
位置公差は、形や角度に加え、形体のあるべき位置も規制可能です。
位置公差は主にデータムに関連する「関連形体」に指示されるため、基本的にはデータム指示が必要です。
位置公差の種類
表1のように、位置公差には主に3つの種類があります。
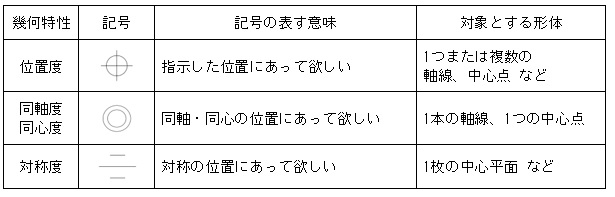
【表1 位置公差の種類】
上記の位置公差によって、形状・姿勢公差では規制できない、対象形体の位置を規制できます。
次項から3つの位置公差について解説していきます。
2.位置度
(1)位置度とは
「位置度」は、形体に対して「指定した位置にあって欲しい」と指示する幾何公差です。
位置度で規制できる形体は1つまたは複数の軸線や中心点であり、ある形体を包む円筒や角柱、円や球の領域などが公差域になります(図1参照)。
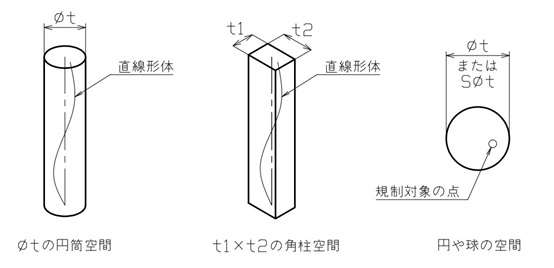
【図1 位置度の公差域】
また、位置度には「真位置度理論」が適用されます。
「真位置」とは、「姿勢公差」の回で説明した「理論的に正確な寸法」のことで、形体の理想的な位置を表します。そのため図面指示において、理想の位置を示す寸法は、四角で囲む必要があります。
(2)位置度の使い方
位置度は、主に穴の正確な位置を規制したい場合に使います。
3つの基準面から正確な距離に穴があって欲しい場合を想定し、基準面からの穴位置のズレは0.1mmまで許容できるとします。
まず図2のように、該当する3つの基準面A、B、Cにデータムを指定します。
穴位置に関しては軸線が規制対象となるので、直径寸法の延長線上に位置度を指示します。
データム平面B、Cから穴までの距離は、理論的に正確な寸法のため四角で囲みましょう。
なお、データム平面Aに関連する寸法はないため、この場合は距離が0とみなされ、データム平面A上から直角な公差域が始まることを意味します。
また、このとき公差域の方向を気にしない場合は、公差値の前に直径記号φを付ける必要があります。
しかし、データム平面B、Cからの距離において、それぞれ別の公差を指示したいのであればφを付けません。
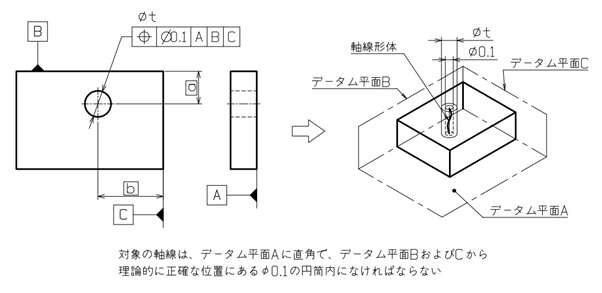
【図2 位置度の図示例と解釈】
(3)コスト削減に役立つ「最大実体公差方式」の使い方
「最大実体公差方式」とは、サイズ公差と幾何公差との間に、特別な関係性を持たせる方法のことです。
この方法を位置度に適用することで、加工コストの削減につながります。
2本の軸が付いた板と2つの穴があいた板とを、はめあいによって組み付けたい場合を例に出します。
このような部品は、軸径が穴径より小さくても、それぞれの位置がズレていると組み付けられないため、位置度を用いるとよいでしょう。
図3は、最大実体公差方式を適用しない場合を示しています。
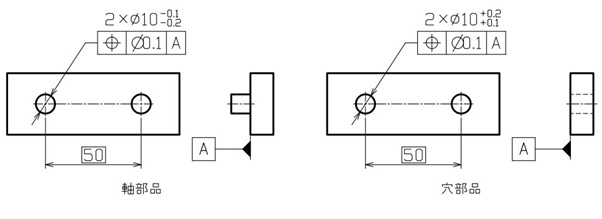
【図3 最大実体公差方式を適用しない場合の図示例】
図3のような図面で、軸径が一番大きく穴径が一番小さい状態(※これを「最大実体状態」と呼ぶ)かつ、図4に示すように、軸と穴のピッチが互いに反するように仕上がったとします。
このとき、軸と穴のスキマは0になり、最大実体状態でも2つの部品が組み付くように位置度公差が設定されていると分かります。
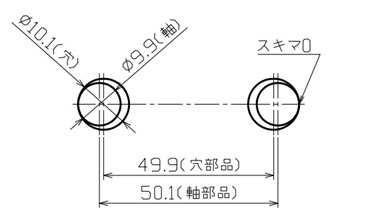
【図4 最大実体状態における軸と穴の位置関係】
一方で軸と穴のピッチが互いに反していても、軸径が一番小さく穴径が一番大きい状態(※「最小実体状態」と呼ぶ)に仕上がった場合は、図5のように、0.1mmの余分なスキマが生じます。
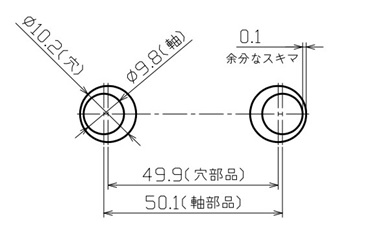
【図5 最小実体状態における軸と穴の位置関係】
最大実体公差方式とは、この余分なスキマを幾何公差に加えて、公差を緩める手法になります。
必要以上に公差を厳しく仕上げなくていいので、加工コストを抑えられるわけです。
最大実体公差方式を適用するには、図6のように公差値の後へ「マルM」を付けてください。
これによって「軸径と穴径のサイズ公差は守って欲しいが、軸と穴の間にできたスキマ分は位置度公差を緩めてもいい」という意図を伝えられます。
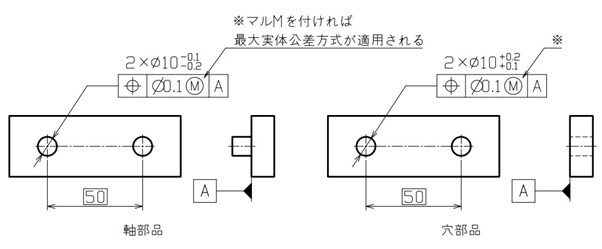
【図6 最大実体公差方式を適用した場合の図示例】
3.同軸度・同心度
(1)同軸度と同心度とは
「同軸度」「同心度」は、その名の通り「同軸・同心であって欲しい」と形体に対し指示する幾何公差です。
図7に同軸度と同心度の公差域を示します。
同軸度が規制する対象は1本の軸線であり、その軸線を囲む円筒空間が公差域になります。
一方、同心度が規制するのは1つの中心点で、その中心点を囲む2次元上の円空間が公差域です。
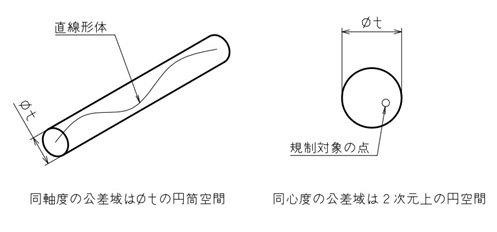
【図7 同軸度・同心度の公差域】
使い分け方として、軸線を規制する場合は同軸度、中心点を規制する場合は同心度と覚えておくとよいでしょう。具体的には、厚みや長さのある円筒部品には同軸度を使い、薄い円形部品には同心度を用います。
(2)同軸度の使い方
同軸度は、旋削加工を行う段付き軸に使われます。
図8のように、段付き軸において、片方の段差部を基準とし、もう一方の段差部が同一軸線上にあって欲しい場合を例として挙げます。基準となる軸線からの位置ずれは0.1mmまで許容できるとします。
軸線が基準なので、基準としたい軸の直径寸法の延長線上にデータムを指定してください。加えて、規制対象も軸線なので、該当の軸における直径寸法の延長線上に同軸度を指示します。
データムが軸線だけを指定していると、座標がなく方向が決まらないため、全周方向を示すφを付けます。
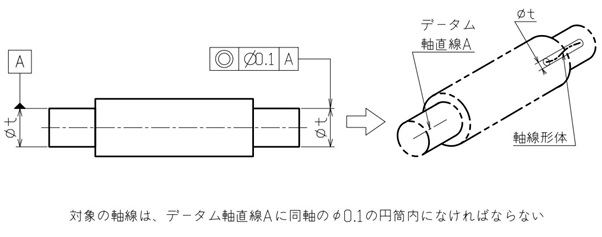
【図8 同軸度の図示例と解釈】
(3)同心度の使い方
薄い円形部品において「外径」と「中心にあいた穴」が同心上にあって欲しい場合を想定します。穴の中心点を基準に、外径の中心点との位置ズレは0.1mmまで許容できるとします。
この場合には、図9に示したように中心点が基準のため、穴の直径寸法の延長線上にデータムを指定してください。同様に規制対象も中心点なので、外径寸法の延長線上に同心度を指示します。
データムの対象が1つの点で座標がないため、同軸度と同じように公差値の前へ全周方向を示すφを付けてください。
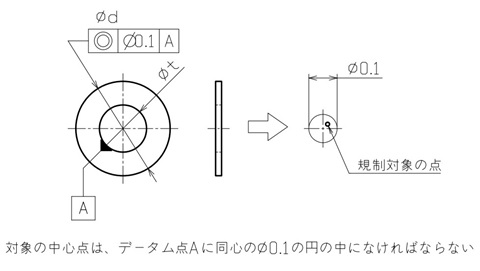
【図9 同心度の図示例と解釈】
4.対称度
(1)対称度とは
「対称度」は、ある形体に「対称であって欲しい」と指示する幾何公差です。
対称度で規制する形体は、図10で示されるように2つの平行な平面によって決まる中心平面などです。
対象度の公差域は、中心平面を挟む平行2平面間になります。
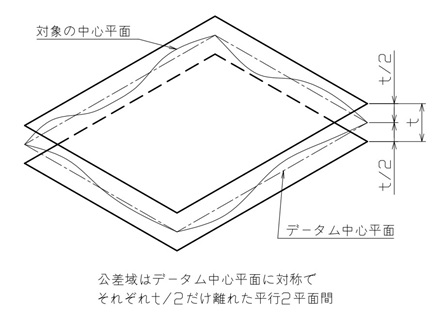
【図10 対称度の公差域】
(2)対称度の使い方
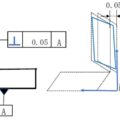
図11のように、切り欠きのあるブロックの中心平面に対して、切り欠きの中心平面が対称であって欲しい場合を想定します。基準となる中心平面からの対称のズレは、0.1mmまで許容できるとします。
指示対象が中心平面なので、基準にするブロックの長さ寸法の延長線上にデータムを指定してください。
同様に、切り欠きの中心平面に対する対称度の指示も、長さ寸法の延長線上に行います。
公差域は平行2平面間になるので、公差値の前にφは付けません。
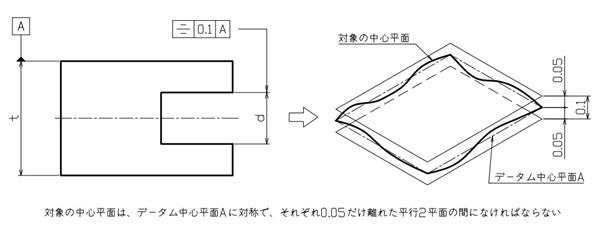
【図11 対称度の図示例と解釈】
以上、今回は「位置公差」(位置偏差)の特徴や使い方を説明しました。
次回は、回転部品に対して用いる「振れ公差」について解説します。
また、アイアール技術教育研究所では本コラム以外にも、定期的に開催されるWebセミナーやeラーニング講座で、幾何公差を学ぶことができます。この機会にご利用してみてはいかがでしょうか?
(アイアール技術者教育研究所 Y・D)
《参考文献・サイト》
- 「図面って、どない描くねん! LEVEL2(第2版)」(2017)日刊工業新聞社
- 「設計者は図面で語れ! ケーススタディで理解する幾何公差入門」(2020)日刊工業新聞社
- 「実用設計製図 幾何公差の使い方・表し方(第2版)」(2019)日刊工業新聞社
- 「幾何公差:設計に活かす「加工」「計測」の視点」(2015)森北出版
【連載】幾何公差を学ぶコラムシリーズ(全6回)
- ゼロから学ぶ 幾何公差図面の読み方[藤崎 淳子 講師]
- 幾何公差の基礎と実践活用《演習付き・1日徹底習得》[小畠 祥平 講師]