【機械設計マスターへの道】運動量の法則［流体力学の基礎知識⑤］

Tweet

Pocket

煩雑な数値計算によらずに比較的簡単に流れの現象を把握することができて、流体が管や板などの様々な形状の物体に及ぼす力を求めることができる「運動量の法則」とその適用例についてご紹介します。

１．ニュートンの法則

まず、力学の基礎となるニュートンの法則について再確認します。

第１法則：慣性の法則

外部から力が作用しない限り、動いている物体は動き続けようとし、止まっている物体は止まり続けようとする性質のこと。

第２法則：運動の法則

物体に力F［N］を加えて物体が運動するとき、
物体の質量をm［kg］、加速度をα［m/s²］とすると、
　F = mα　　・・・(1)
の関係になる。

第３法則：作用・反作用の法則

物体に力を加える（作用）と、逆方向に同じ大きさの力を受ける（反作用）こと。

２．運動量の法則

質量m［kg］の物体が速度v［m/s］で運動しているとき、運動量Mは、
　M=mv ［kgm/s］　　・・・(2)
で定義されます。

速度の1回微分は加速度ですから、（1）（2）式より
　F = m dv/dt =d/dt(mv) =dM/dt　　・・・(3)

すなわち、運動量の時間的な変化割合は、その物体に及ぼす力に等しくなります。
この(3)式を運動量の法則といい、質点の集合体とみなすことができる連続体の流体要素にも適用することができます。
 

検査面と検査体積、運動量の式

簡単にするために、定常流の状態に限定して考えてみます。

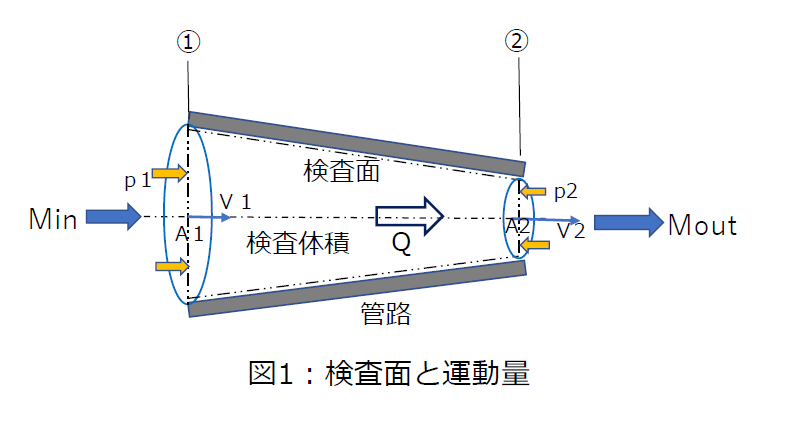
図1で、管路を切断する断面①，②と管路内壁面で囲まれる仮想の境界面を「検査面」、検査面で囲まれる領域を「検査体積」、検査体積内の流体要素を「系」といいます。

検査面①を通って検査体積に入る運動量をMin、検査面②を通って検査体積から出る運動量をMoutとすると、系における運動量変化量⊿Mは、
　⊿M=Mout-Min　　・・・（4）
となります。

断面①，②の断面積、平均流速、密度をそれぞれ、A₁,A₂,v₁,v₂,ρ₁,ρ₂ とします。
断面①から入る流体は、微小時間⊿tの間に距離v₁⊿t だけ移動し、流体質量m₁=ρ₁A₁v₁⊿tが平均流速v₁で入りますから
　Min=m₁v₁=(ρ₁A₁v₁⊿t) v₁　　・・・(5)
同様に、断面②から出る運動量は、
　Mout= m₂ v₂=(ρ₂A₂v₂⊿t) v₂　　　・・・(6)
となります。

ここで各断面を流れる流量をQ₁,Q₂とすれば、Q₁= A₁v₁、Q₂= A₂v₂であるので、式(3),(4),(5),(6)より、検査体積内の流体に作用する外力Fは、
　F=dM/dt=(Mout-Min)/⊿t =ρ₂Q₂v₂-ρ₁Q₁v₁=(ρQv)_out-(ρQv)_in　　　・・・(7)　

すなわち、定常流において、検査体積内の流体に及ぼす力は、検査面上の断面を通して単位時間に流出入する運動量の変化に等しくなります。
（7）式を運動量の式といい、粘性や圧縮性のある流体に対しても適用することができます。
非圧縮性流体であれば密度ρを一定として扱うことができます。
連続の式より非圧縮性流体の場合は Q= A₁v₁= A₂v₂=const. ですから、（7）式は、
　F=ρQ(v₂-v₁)　　　・・・(8)
と表すことができます。
つまり、質量流量に速度差をかけた値の力が外力として検査体積内の流体に作用するということになります。

ニュートンの第3法則（作用反作用の法則）により、Fと値が同一で、方向が逆向きの力が物体に作用します。
図1で検査体積を囲む物体が管路であれば、管路に-Fの力が反作用としてかかることになります。

(8)式は、Q=A1V1=A2V2 の関係により、図のような A2＜A1 の形状のノズルであれば V2＞V1 になりますから、Fの方向は図の右向き（+方向）になります。
管路は、Fの反作用として‐Fの力を図の左向き（-方向）に受けます。
 

検査面の断面積や圧力が異なる場合

検査面の断面積あるいは、検査面に作用する圧力が異なる場合は、運動量による力の他に、圧力による力fpを考慮する必要があります。

図1の場合、fpは検査面上の断面①，②において圧力によって働く表面力で
　fp= A₁p₁– A₂p₂　　　・・・(9)
となります。
(9)式は、流体がもつ圧力により、検査面上の流入出面を通じて管路におよぼす力であり、入出面における圧力と断面積の積が圧力による力になります。

したがって、検査体積内の流体が管路に及ぼす力をfとすれば(8)、(9)式より
　f=fp-F= A₁p₁– A₂p₂ + ρQ(v₁-v₂)　　　・・・(10)
となります。
管路が受ける力fは、圧力による力fpと、流体から受ける運動量による力の反作用‐Fの合計となりますので、(10)式の通り f=fp-F となります。

３．運動量の式の適用例

（１）消防ホースノズル

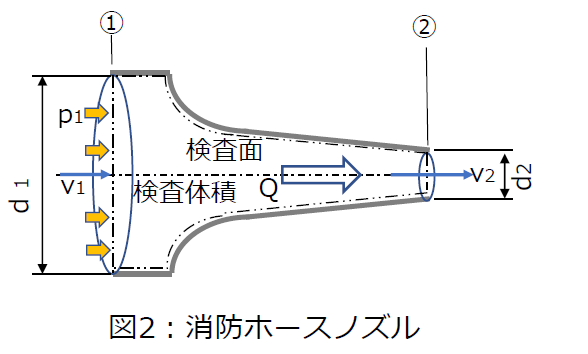
図２のような入口直径d₁=40［mm］, 出口直径d₂=13［mm］の消防ノズル先端から、入口圧力p1=0.2［MPa］で水が大気中に放水される状態を考えます。
水がノズル内面に囲まれるような検査体積と検査面をとります。検査面の水の流入口を断面①、流出口(放出口=大気圧)を断面②とします。
流量をQ(m³/s)とすれば、「連続の式」（本連載コラム「連続の式とベルヌーイの定理」の回を参照）より
　Q= A₁v₁= A₂v₂ したがって　v₁= (A₂/ A₁) v₂　　　・・・(11)
ノズル出口は大気圧ですので出口圧力p₂=0となります。

ベルヌーイの式より、
　v₁²/2+p₁/ρ= v₂²/2　したがって p1=(ρ/2)( v₂²– v₁²)　　　・・・(12)

（11）,(12)式よりv₁を消去してv₂について解けばv₂=20.1［m/s］となります。
ただし、ρ=1000［kg/s］(常温水)

A²=(π/4)(d₂x10^-3)²=1.33 x10^-4［m²］ A₁=(π/4)(d₁x10^-3)²=1.26 x10^-3［m²］
Q= A₂v₂=1.33 x10^-4 x 20.1=2.67×10^-3［m³/s］（=160リッター毎分）
v₁=Q/A₁=2.67×10^-3/((π/4) (d1x10^-3)² =2.12 m/s (d₁=0.04［m］)
(10)式より、ノズルが流出する水から受ける力fは、
f= A₁p₁ +ρQ(v₁-v₂)= 1.26 x10^-3x0.2×10⁶+1000×2.67×10^-3x(2.12-20.1) =203［N］となります。

（２）噴流がタンクに及ぼす力とロケット推進の原理

図3のようなタンク側面の底部に小孔があって、水が噴出しているとします。
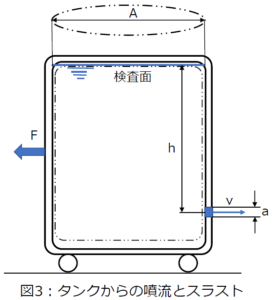
簡単のため水面高さhは一定に保持されていると仮定します。タンク内面を囲むように検査面を取ります。タンク断面積Aに比較して小孔の断面積aが十分小さい場合、噴流の速度vは、
　v=√2gh　　　・・・(13)
で求めることができます。これを「トリチェリの定理」といいます。

噴流には縮流という現象が生じるため、噴流の断面積は小孔の断面積aよりも小さくなり、流量を求める際に流量係数をかける必要があります。
ここでは簡単のため、流量係数を1とすれば、
　流量Q=av　　　・・・(14)
検査面にかかる圧力は各方向に対して一定ですから、運動量の式より、タンクが噴流から受ける力F（反作用力）は、
　F=ρQv=ρav²=2gρah　　　・・・(15)
このタンクが噴流から受ける力Fを「推力」（スラスト）といいます。
ロケットの推進機構は、この原理に基づいています。

 
今回ご紹介した運動量の法則は、検査体積を適切にとることで、検査体積の境界面である検査面から流出入する流体に対して、各検査面の断面積、断面の圧力、密度、流量、流速を知ることができれば、（対象とする物体の内部状態がわからなくても）物体が流体から受ける力を求めることができる便利な手法です。
ぜひ設計等の実務でご活用ください。

 
次回の連載コラムでは、物体まわりの流れとカルマン渦について解説いたします。
 
（日本アイアール株式会社　特許調査部　S・Y)
 

＜参考文献＞

• 　西海孝夫 著『図解　はじめて学ぶ　流体の力学』 日刊工業新聞社、2010

※本コラムで基礎を概説した流体力学についてさらに深く学びたい方に、おススメの書籍です。

Tweet

Pocket