【機械製図道場・上級編】幾何公差の図示を習得！幾何公差の種類・特性・記号は？データムって何？

Tweet

Pocket

今回は、幾何公差についての解説と例題演習を行います。

「幾何公差」とは、品物の形状の幾何学的な精度を示す指標で、設計で意図する形状からのずれ（ゆがみ）の程度のことです。

これまでの連載で学んだ寸法公差は、寸法数字の許容誤差範囲を数値で規定します。
一方、幾何公差は形状のゆがみ具合の許容値を数値で規定します。
世界標準では幾何公差が主流となっており、JIS製図規格も、幾何公差をより重視する方向へシフトしています。幾何公差を適正に設定することにより設計要求の曖昧さをなくすことができる利点があります。
幾何公差についてしっかり理解して図面に反映するようにしましょう。

１．幾何公差の種類と記号

（1）単独形体

その形状に対して、単独に指定できるものを「単独形体」と呼び、単独形体に関する幾何公差を「形状公差」と呼びます。
「形状公差」には、下表のような6つの特性があり、それぞれ以下の記号で表します。

（2）関連形体［姿勢公差/位置公差/振れ公差］

幾何公差を設定するために、何か基準となる相手との関係が必要になるものを「関連形体」と呼びます。

関連形体に関する幾何公差には、「姿勢公差」「位置公差」「振れ公差」の3種類があります。
それぞれの特性と記号は下表の通りです。

２．データムとは？

関連形体幾何公差の定義には、「データム」という用語が使われています。
データムとは、関連形体幾何公差を決めるために設定された理論的に正確な幾何学的基準のことで、「指定された幾何公差に基づいて加工や検査をする際は、この面または線を基準としてください」、という意味です。

３．幾何公差の図示方法

（1）幾何公差記入枠

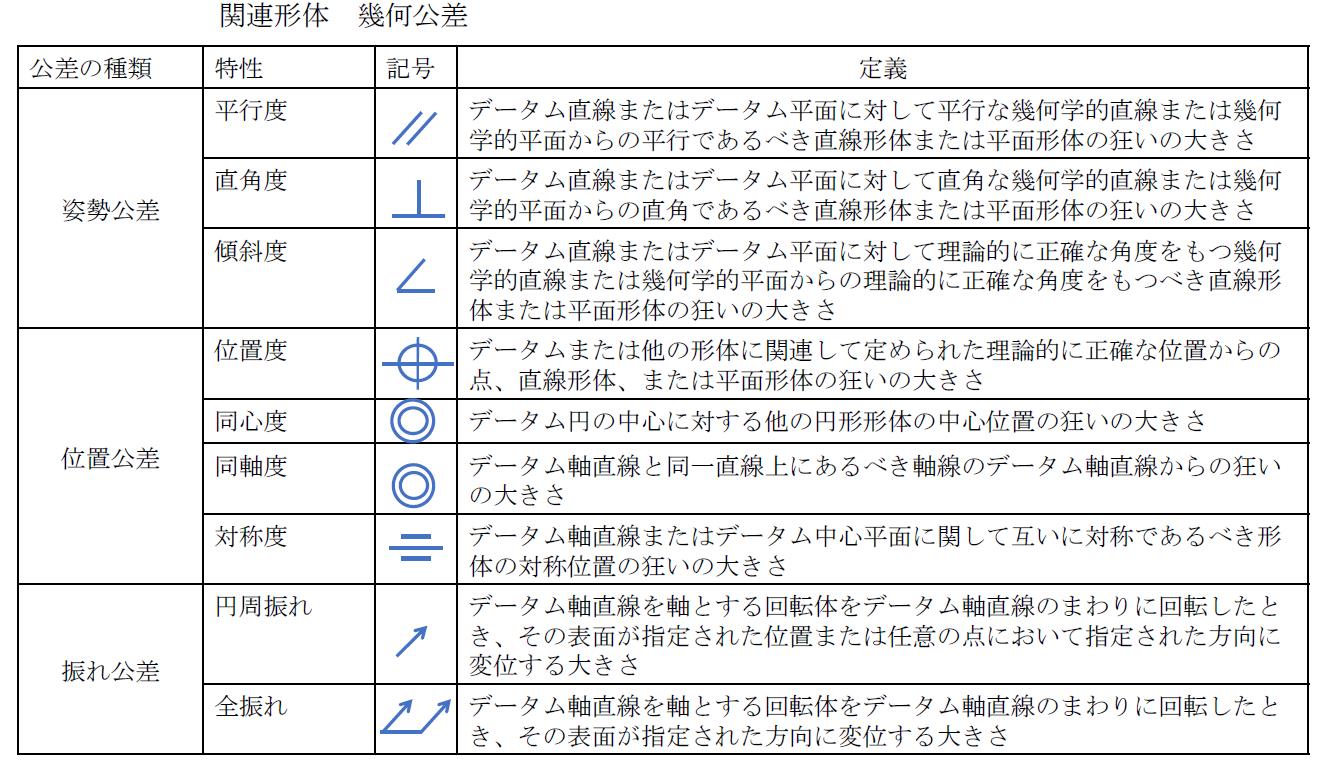
下図のように、左に幾何公差の特性記号、右側に公差値を記入します。
データムを指定する関連形体の場合は、公差値記入枠の右にデータム指示記号を大文字アルファベットで記入します。
データム指示記号は、基準形体または寸法線に対向して▲記号と指示線でつないで表示します。

（2）図面指示

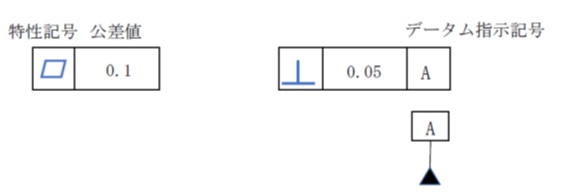
線または面を対象とするときは、外形線に指示線を垂直にあてて幾何公差記入枠と結びます。
軸線または中心平面に対して幾何公差を指示する場合は、寸法線と一直線上に対向させて指示線を引き出します。公差記入枠は、必ず水平に配置します。

【左：面を対象とする表示／右：軸線を対象とする表示】
 

（3）幾何公差図示の例と意味

① 形状公差の例

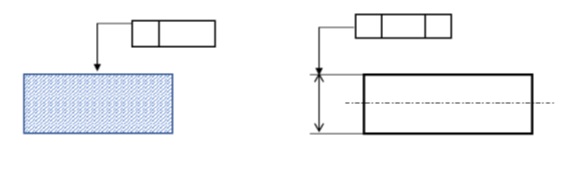
平面度の図示例です。実線で表された上の面を、幾何学的平面から0.1mm以内のゆがみで仕上げることを要求しています。

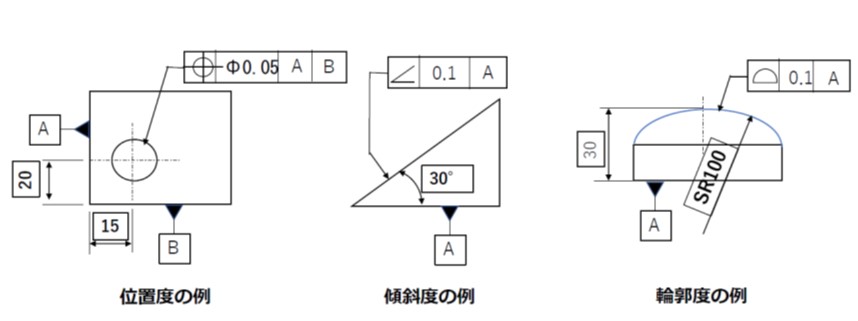
② 姿勢公差の例

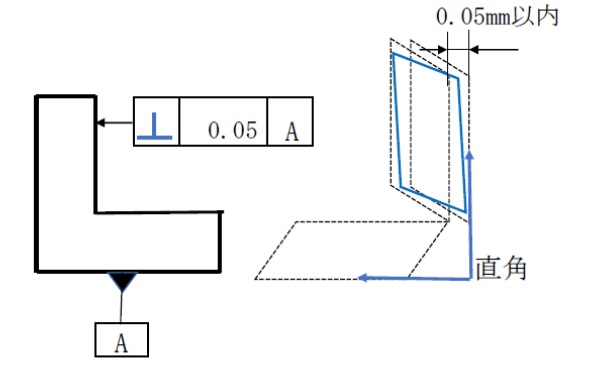
直角度の図示例です。下面をデータム（基準形体）として、右の垂直面を、データムに対して幾何学的に直角な平面から0.05mm以内の狂い（倒れ）で仕上げることを要求しています。

③ 位置公差の例

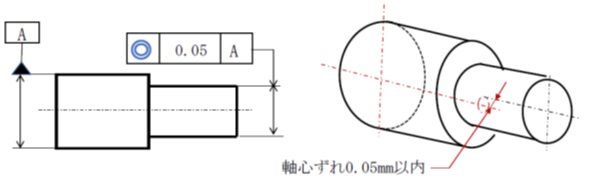
同軸度の例です。径の大きいほうの円筒部の軸心をデータムとして、径の小さいほうの円筒部の軸心のずれが、0.05mm以内に収まることを要求しています。
なお、軸心ではなく平面上の円中心のずれに対する幾何公差を同心度とよび、同一の記号を使用します。

④ 振れ公差の例

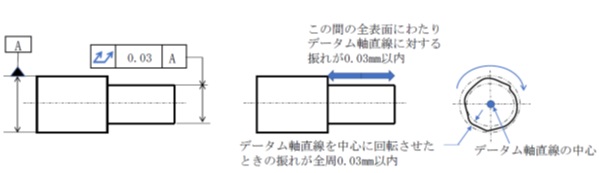
全振れの例です。円筒を軸心まわりに回転すると表面の微細な凹凸により、断面には真円からのずれが生じます。これを「振れ」といいます。

図のように、対象物をデータム軸直線まわりに回転したときの振れを、対象とする円周面の全長にわたって公差内に収めることを要求する場合を全振れといいます。
対象円周面の任意の位置の振れの場合を円周振れといいます。

（4）二つのデータム形体によって設定する共通データム

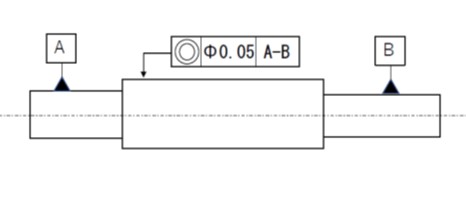
一つのデータムをふたつの形体によって設定するときは、図のようにハイフンで結んだ文字記号によって表示します。
下図の例では、両側の二つの円筒部の軸心をデータムとして、中央の径が大きい円筒部の軸心のずれが、0.05㎜以内に収まることを要求しています。

（5）二つ以上のデータムによって設定するデータム系

二つ以上のデータムを組合せて設定するデータム系の場合は、優先度の高いデータムから順に左において表示します。
図の例では、板にあける穴の位置度が、底面に対して直径0.05の円筒公差域内にあることを第1優先要求としています。

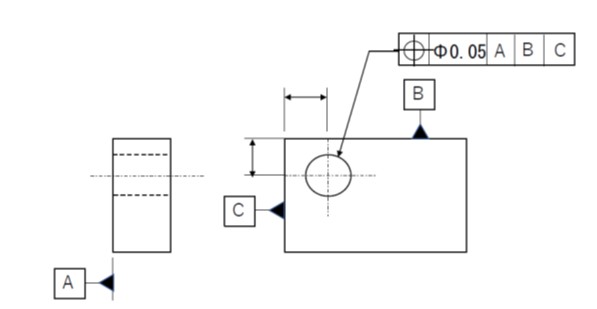
（6）理論的に正確な寸法

位置度、輪郭度、または傾斜度の公差を指定するとき、その位置、輪郭、傾斜、を指定する寸法のことを理論的に正確な寸法といい、寸法公差を設けずに、四角い枠内に囲んで表示します。

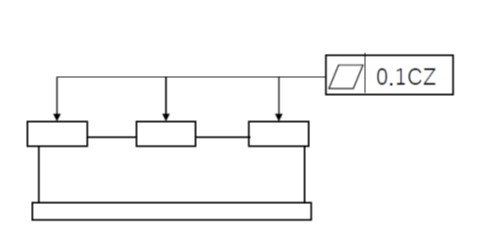
（7）共通公差域

共通公差域記号CZをつけることにより、複数の離れた形体に対して、共通の公差域を適用して、形体間の相対的な位置関係も規定することができます。
下図の例では、離れた3つの面の平面度を、共通の幾何学的平面から0.１㎜以内のゆがみで仕上げることを要求しています。

では、簡単な例で演習してみましょう。
 

【例題】要求幾何公差に応じた製図

《 問題 》

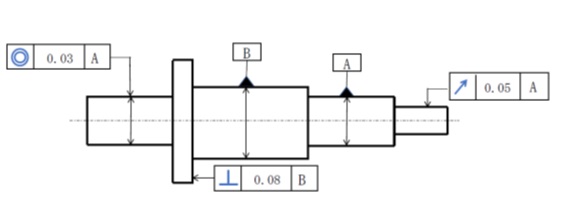
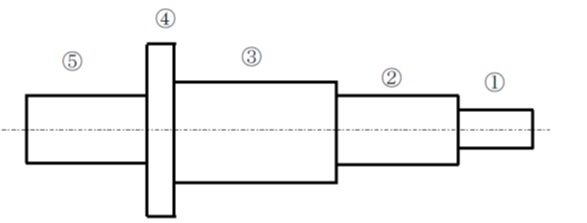
図のようなシャフトがあります。

②の軸心を回転中心として回転したとき
①の円周上任意の点の振れを0.05mm以内、
②に対する⑤の軸心ずれを0.03mm以内、
③の中央部軸心に対する④の右端面の直角度を0.08mm以内、
とする必要があります。

これら要求幾何公差を正しい方法で製図してください。

《 解答 》

解答例はここをクリック

《 例題の解説 》

【関連知識】データムの設定方法、公差の緩和

（1）データムの設定方法

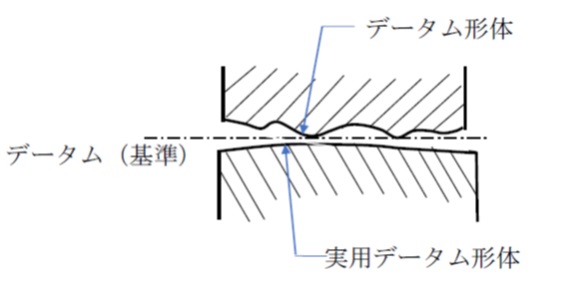
データムは幾何学的に正確な面または軸線として設定しますが、図面にデータムを指示しても、製作誤差が生じます。

実際には、データムとする面に定盤など十分精度の高い形状をもつものを接触させて、回転軸芯は軸受けやマンドレルなど精度の高い保持部品を用いて、データムを設定します。

測定対象物のデータムに指定した面や線を「データム形体」、定盤、軸受け、マンドレルなど基準とする側の面や線を「実用データム形体」といいます。

（2）公差の緩和

① 最大実体公差方式

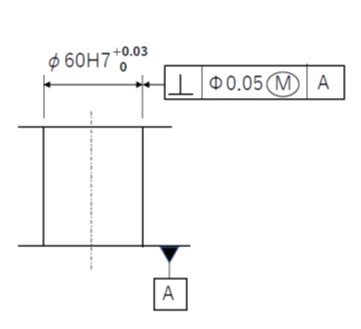
寸法公差と幾何公差の両方を表示する場合に、両者の相互依存関係を考慮する方法で、軸線または中心平面に適用し、円内にMの記号で指示します。
図の例で、直径60の穴の下平面に対する直角度要求が 0.05 です。
最小実効寸法は 60 – 0.05 = 59.95 ということになります。
穴径の公差は +0.03～0 であり、59.95 の最小実効寸法を確保するための直角度公差域は 60.03－59.95=0.08 となります。
つまり、穴径を寸法公差の上限まで大きくした場合、幾何公差をその分緩和できることになります。
最大実体公差方式は、軸と穴などの干渉を防止しつつ、加工条件を緩和したい場合に有効な手法です。

② 最小実体公差方式

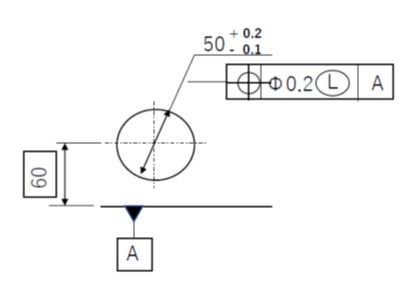
最大実体公差方式と同様に、寸法公差と幾何公差の相互依存関係を考慮する方法であり、円内にLの記号で指示します。
図の例で、直径 50（公差+0.2～-0.1) 穴の中心のデータム面からの理論的に正しい寸法 60 に対する位置度要求が φ0.2 です。最小板厚は 60 – 50.2 / 2 – 0.1 = 34.8 ということになります。
穴径が公差下限の 49.9 のとき、34.8 の最小板厚を確保するための位置度公差域は (60 – 49.9 / 2 – 34.8) x 2 = φ0.5 となります。
つまり、穴径を寸法公差の下限まで小さくした場合、幾何公差をその分緩和できることになります。
最小実体公差方式は、必要肉厚を確保しつつ、加工条件を緩和したい場合などに有効な手法です。

寸法公差が許容値内に収まっていても、形状の歪みがあると機械の機能が損なわれることがあります。

様々な幾何公差の意味するところを正しく理解して、必要な幾何公差を適確に図面に指示するように心がけてください。
 
（アイアール技術者教育研究所　S・Y）

Tweet

Pocket