バンド構造とフェルミ準位の基礎知識|フェルミ分布関数、電子密度の温度依存性などをわかりやすく解説
![]()
連載「これならわかる半導体超入門」の第3回は、バンド構造とフェルミ準位について解説します。
目次
1.電子のふるまいにおける温度の役割
当連載コラムの第1回の「そもそも半導体とは?」で述べた導体、絶縁体、半導体を、バンド構造という視点から見直してみましょう。その際に、温度の役割が重要ですので、先ず、温度が電子の振る舞いとどのように関係するのかを説明します。
本コラムの第2回「半導体における電子のふるまい」では、「有限の温度(例えば室温)ではある確率で、電子が価電子帯から伝導帯に励起される」と述べました。
これは、
熱エネルギーをもらった価電子帯の電子は、ある確率で伝導帯に飛び上がるが、伝導帯の方がエネルギーが高いので、すぐにエネルギーの低い(安定な)価電子帯に落ちてくる。しかしその間に他の電子が伝導帯に飛び上がっているので、ならしてみれば、常に一定数の電子が伝導帯にいることになる。
と解釈することができます。

電子がどのようにして熱エネルギーを貰うかは、次のようなイメージです。
結晶の場合であれば、温度が高いと各原子の運動(振動等)が激しくなる。原子の運動によって電子の分布も影響をうける、すなわち電子のエネルギー状態も変わる。
伝導帯にいる電子の数は、温度が高いほど(飛び上がるエネルギーが大きいほど)、またバンドギャップが小さいほど(飛び上がる高さが低いほど)多くなるであろうことは容易に推測できます。これが絶縁体と半導体の程度の差です。
より正確には、ある温度Tで特定のエネルギーEの準位に電子が存在する確率は、下のフェルミ分布関数(F)に従います。
F(E) = 1/(1+exp((E-Ef)/kT))
kは「ボルツマン定数」と呼ばれ、絶対温度(T)とエネルギーを関係づける物理定数です。
2.フェルミ準位とは?
ここで、Efは「フェルミ準位」と呼ばれ、EがEfに等しい場合F(E)が1/2となるようなエネルギー準位です。
フェルミ準位も温度に依存します。
絶縁体や半導体では、フェルミ準位は禁制帯のほぼ中央に位置し、有限の温度での伝導帯、価電子帯での電子の濃度は模式的に図1のように示されます。
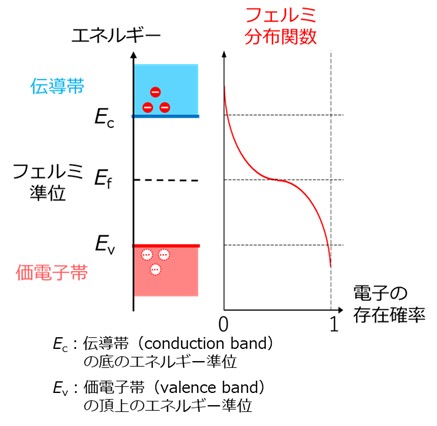
【図1 絶縁体、半導体における電子の伝導帯、価電子帯での濃度とフェルミ分布関数との関係】
フェルミ分布関数は、 F(E) = 1/(1+exp((E-Ef)/kT)) の式から、有限の温度では、
E → +∞ で、F(E) → 0
E → -∞ で、F(E) → 1
となります(図の赤線)。
図のように、有限の温度では、伝導帯の底にわずかに電子が存在し、価電子帯の頂上にわずかに電子が抜けた孔が存在します。この孔は「正孔」(ホール)と呼ばれ、電子が存在している状態で電気的に中性である場所に電子が存在しないため、プラスに帯電しているかのようにふるまいます。
3.電子密度の温度依存性
絶対零度では伝導帯は完全に空っぽで、価電子帯は完全に電子で埋まっているため、この半導体に外部から電圧をかけても電流は流れません。
しかし、有限の温度(例えば室温)では、伝導帯に上がった電子は自由に動け、価電子帯の電子も正孔の位置が移動するという形で自由に動けるため、外部からの電圧に応じて電流が流れます。
図2はバンドギャップ(Ec-Ev)が1.12eV *1)であるシリコンの伝導帯の電子密度の温度依存性です。
フェルミ分布関数は、E-EfがkTより十分大きいとき、
F(E) = 1/(1+exp((E-Ef)/kT))
~1/exp((E-Ef)/kT) = exp(-(E-Ef)/kT)
と変形できるので、横軸に1/T、縦軸に電子濃度の対数をとると直線関係になります。
室温の目安である27℃の時と、100℃の時ではシリコンの電子濃度が2桁も違うという感じを掴んでください。
![]()
【図2 シリコンの伝導帯の電子密度の温度依存性】

4.金属中の電子の状態(バンド構造)
では、導体の代表である金属では何が起こっているのでしょうか?
ここでも、正確に理解するためには量子力学の知識が必要ですが、イメージとしては金属原子の最外殻電子は原子核との結合が緩く、金属結晶全体に広がった状態になっており、広がった電子の雲の中に原子核が包まれたような状態で結合しているのが金属結合です。この状態をバンド構造で表せば次のようになります。
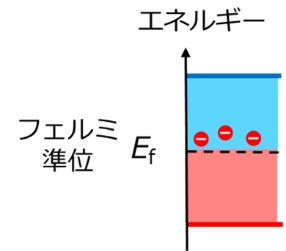
【図3 金属のバンド構造】
バンドの下部には電子が詰まっていますが、上部は空になっています。
別の言い方をすれば、フェルミ準位がバンドの中にあり、このため、自由に動ける電子は多量にあるので金属は良導体になります(図3)。
また、動ける電子の数は温度によりません。一方で電子の動きやすさ(移動度)は温度が高くなるほど小さくなります。原子核が振動するため電子がスムーズに動きにくくなるというイメージです。
このため温度が高いほど、絶対温度に比例して抵抗は大きくなります。
電気伝導度の温度依存性からみた 導体/絶縁体/半導体 の違い
あらためて、導体(金属)、絶縁体、半導体の違いを、電気伝導度の温度依存性から確認しましょう。
横軸に絶対温度の逆数、縦軸に電気伝導度の対数を取った図4で、金属は伝導に寄与する電子の数が温度によらず、低温ほど電子は動きやすくなるのでわずかに右肩上がりになります。
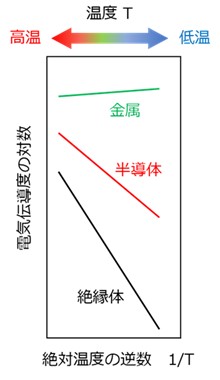
【図4 導体(金属)、半導体、絶縁体の電気伝導度の温度依存性】
半導体と絶縁体は、伝導に寄与する電子の数が、温度の逆数に指数関数的に依存するため、大きな温度依存性(桁の違い)を示し、その程度はバンドギャップの大きさによって決まっています。半導体、絶縁体でも電子の動きやすさは温度の影響を受けますが、電気伝導度に与える影響は、数の方がはるかに大きいのです。
このように半導体と絶縁体は「程度の差」ですが、第4回のコラムで説明する不純物半導体は、様相がかなり違います。
5.まとめ(おさらい)
今回のコラムでは以下のことをご説明しました。
- 絶対零度では半導体の伝導帯に電子はいないが、有限の温度では、一部の電子は伝導帯に上がる。
どの程度の電子が伝導帯に上がるかは、下のフェルミ分布関数に従う。
F(E) = 1/(1+exp((E-Ef)/kT)) - Efはフェルミ準位と呼ばれ、EがEfに等しい場合F(E)が1/2となるようなエネルギー準位である。
- 金属ではフェルミ準位がバンドの中にあり、自由に動ける電子が多量にあるため良導体になる。
次回は、n型半導体・p型半導体(不純物半導体)について解説します。
(アイアール技術者教育研究所 H・N)



































