メタマテリアルとは？原理/構造/応用例などをわかりやすく解説《透明マントも実現？》
「メタマテリアル」（metamaterial）は、人工的に作製された複合物質です。電磁波の波長に比べて小さい間隔で周期的に対象を並べたものです。そして、自然界にはない物性や性能を手に入れることができます。
ちなみに、メタ（meta）とはギリシャ語で「超越」を意味しています。
今回は、メタマテリアルの基礎知識を解説します。
目次
１． 前提知識：負の屈折率とは？
メタマテリアルを語る上で欠かせない言葉が「負の屈折率」（図1）です。
長い間、自然界における屈折率は正の値として扱われてきましたが、1967年にV. G. Veselagoが、負の屈折率の概念を提案しました。その後、1999年にJ. B. Pendryらが共振器を用いて負の屈折率を達成できる可能性を示され、2000年にD. R. Smithらがマイクロ波領域において負の屈折率を実証しています。
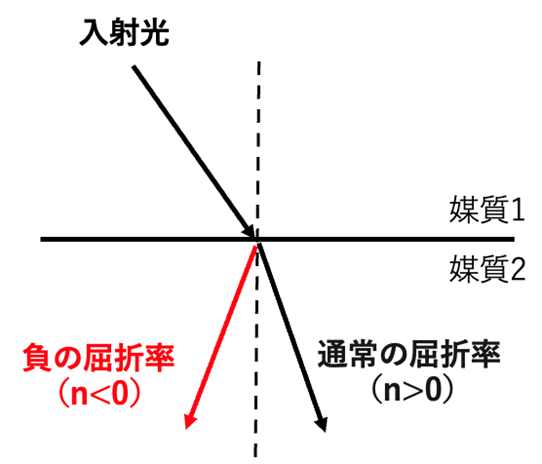
【図1 「負の屈折率」のイメージ】
例えば、水の屈折率は約1.3です。しかし、メタマテリアルの出現により負の屈折率を定義することが可能になると、今までの概念に変化が起き、多くの応用が期待されるようになりました。
（1）光周波数領域における磁気的応答
光は、電場と磁場の２つの波から成ります（図2）。
そして、電場に対する応答特性を「誘電率」、磁場に対する応答特性を「透磁率」で示します。
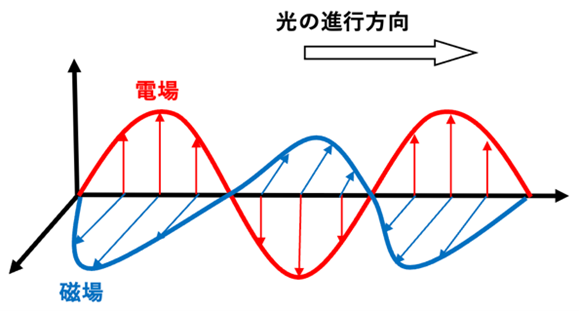
【図2 電場と磁場の関係】
周波数帯によってそれらの応答は異なります。物質の電気的な応答特性は低周波から高周波帯まで存在し、誘電率の値は正から負まで大きく変化します。
一方で、物質の磁気的な応答は高周波帯では存在しておらず、透磁率の値は真空の場合と同じになるため、高周波帯で比透磁率は1.0となります（図3）。
光周波数帯は数百THzと高周波となるため、その領域では電気的な応答のみしか存在しません。つまり、磁気的応答が考慮できずに私たちが利用できる物質の光学特性の幅が狭くなってしまいます。
そこで、人工的に光周波数帯での透磁率に変化を与える制御を行って、物質の光学特性の幅を広げる方法が提案されました。これがメタマテリアルの始まりです。
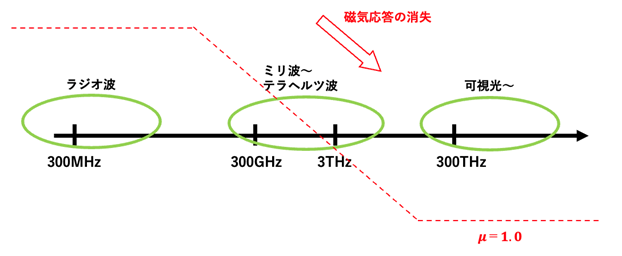
【図3 磁気応答の消失イメージ】
（2）比誘電率、比透磁率と屈折率
「屈折率」は、メタマテリアルを考えるうえで大事なので、ここで今一度確認したいと思います。
屈折率は、スネルの法則から媒質における光の屈折を表現する物理定数です。
そして、次式（1）のように表されます。
・・・（1）
また、比透磁率は次式（2）で表されます。
ただし、α(ω)はほぼ1となる無次元関数（共振近傍を除く）、aは媒質の構成単位の大きさ、λは真空中の波長です。
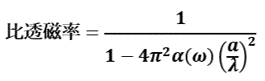・・・（2）
光学が対象とする自然界では原子が主に相互作用に寄与するので、媒質の構成単位の大きさを原子半径で見積もると、可視光領域のλに比べてaは十分に小さくなります。そのため、式(2)から光領域では比透磁率は1になります。通常、自然界の物質では屈折率が1.0〜4.0程度の正の屈折率となっており、自然界の範囲では「負の屈折率」を定義することはできません。
しかし、人工的に作製されたメタマテリアルでは、比誘電率と比透磁率を制御することで負の屈折率を達成させることが可能になります。その制御には共振器を用いますが、メタマテリアルの構造の話にもなりますので、これについては後述します。
さて、比誘電率Eと比透磁率μは角周波数ωに依存しますので、以降比誘電率をE(ω)、比透磁率μ(ω)と記載していきます。そして、それらは周波数領域によってその正負が決まります。この時、屈折率との関係が図4になります。
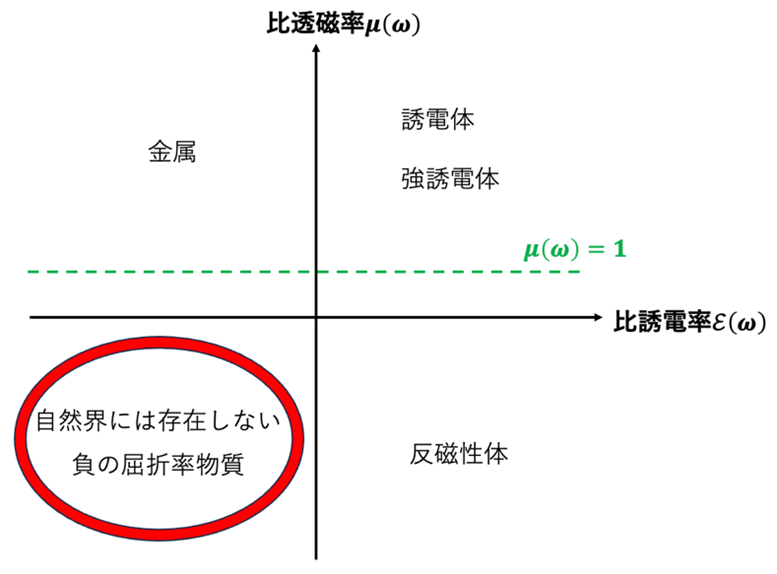
【図4 比誘電率E(ω)と比透磁率μ(ω)の関係 】
図4の各領域は次のようになっています。
第1象限
E(ω)>0,μ(ω)>0 であり、「ダブルポジティブ物質」（double positive material）と呼ばれています。
正屈折率（n>0）であり自然界に存在し、光領域における通常の物質です。
第2象限、第4象限
E(ω)<0,μ(ω)>0 または E(ω)>0,μ(ω)<0であり、「シングルネガティブ物質」（single negative material）と呼ばれています。
自然界において、金属や磁性体では特定の周波数帯で比透磁率と比誘電率の片方が負になる事があるが、同時に負になることはありません。そして、この時の屈折率は虚部を含む複素屈折率となります。
第3象限
E(ω)<0,μ(ω)<0であり、「ダブルネガティブ物質」（double negative material）と呼ばれています。
これは自然界には存在しません。
ここで、注意するべき事があります。それは、メタマテリアルにおける屈折率は共振構造に起因した周波数依存性があることから常に負であるわけではないということです。つまり、特定の周波数帯では負の屈折率（n<0）を示すがそれ以外の周波数帯では正の屈折率（n>0）を示すような物質が存在します。そのため、負の屈折率物質がメタマテリアルと同義であるとは限らない事に注意しなければなりません。
（3）負の屈折率を式で考える
比誘電率と比透磁率が共に負であり、屈折率が負であるとはどういうことかを式から考えてみます。
負の屈折率を考えるために拡張した屈折率nは次式（3）で定義します。
ただし、nは屈折率、E(ω)は比誘電率、μ(ω)は比透磁率です。
・・・（3）
図2の第3象限の場合、つまり、 E(ω)<0,μ(ω)<0を考えると屈折率は次式のように計算されます。
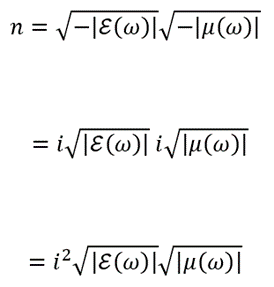
・・・（4）
もし、拡張せずに式（1）から屈折率を計算するとマイナス同士が打ち消しあって、負の屈折率とはなりません。図2の第3象限でご説明したように、周波数特性によってメタマテリアルの屈折率が負となる周波数以外の周波数帯では、式(1)が屈折率として定義され、比誘電率と比透磁率がどちらも負だったとしても負の屈折率は現れません。
なお、負の屈折率が生じるものとして、メタマテリアル以外に「フォトニック結晶」があります。
フォトニック結晶は、光の波長と同程度の周期的な屈折率分布を持つ材料です。この時、負の屈折率は周期と光波長が同程度の際の干渉によるため、メタマテリアルの負の屈折率が生じる理由とは異なります。
２．メタマテリアルの構成・構造
メタマテリアルの構成（構造）はどうなっているのかを説明します。
メタマテリアルは微細加工技術によって作られた共振器で構成されています。
これは、私たちに身近な水が水分子で構成されているのと同じイメージです。そして、それら共振器はメタマテリアルの基本素子であり、「メタ分子」などと呼ばれています。
通常、共振器が三次元的に集積した構造となっています（図5）。
（1）分割リング型共振器とは
共振器は、「分割リング型共振器」 (SRR/split-ring resonator) と呼ばれるものを用いて、比透磁率の制御を行って負の屈折率を実現させる研究が世界中で行われてきました。
SRRは、リングの部分が二重タイプや一重タイプがあります。
一重タイプについては、光の周波数領域で十分な磁気応答を示すために後に提案された方法なので、ここでは基本的な二重タイプについて説明します。
![分割リング共振器の例 ※引用[3]](https://engineer-education.com/wp/wp-content/uploads/2023/11/Meta-Material-01-10.png)
【図5 分割リング共振器の例 ※画像引用[3]】
（2）分割リング型共振器の構造
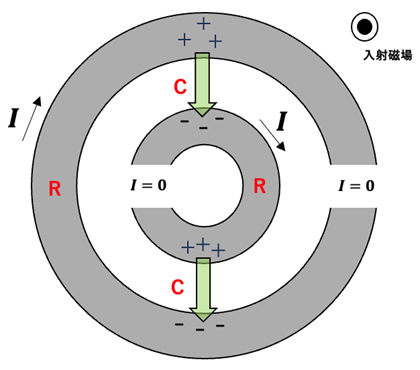
【図6 分割リング型共振器の構造】
SRRの構造は図6のようになっています。電磁波を垂直に入射すると誘導電流Iが流れて、リングが分割されているためにリング内部に電荷が蓄積されます。そして、リング間を電荷が移動するため、LC共振回路が出来上がります。この時、リング部分がコイルの役割（インダクタンスL）、リング間がコンデンサの役割（キャパシタンスC ）となっていて、SRRの共振周波数は式（5）となります。
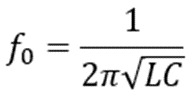・・・（5）
この共振周波数付近で、透磁率は大きく変化します。つまり、共振器を用いたメタマテリアルでは、共鳴条件を整えて透磁率を変化させることで、高周波領域でも負の透磁率を実現できるようになり、負の屈折率も実現できます。
ここで、透磁率は、高周波になると磁性体内の磁束密度の位相が磁界に対して遅れ始めるため、この位相遅れを表すために損失項（虚部）を考える必要があります（参考[4]）。この時、複素透磁率と呼び、ある周波数fで式（6）となります。
・・・（6）
そして、SRRにおける周波数による透磁率変化は図7のようになっています。
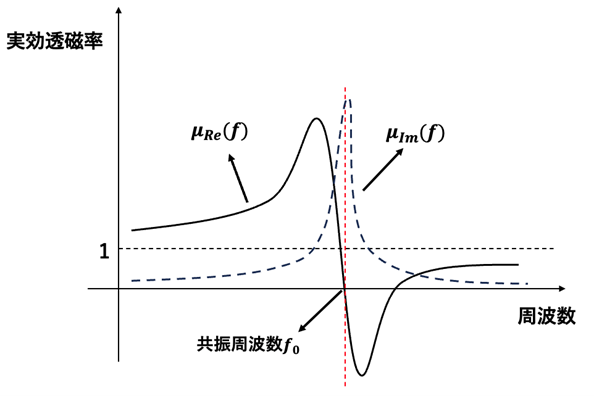
【図7 透磁率変化】
μRe(f)の変化量は、μIm(f)が鋭く変化するほど大きくなります。そして、十分大きな変化が起こると実効透磁率は負になることが可能になります。また、共振器の特性は図5の μIm(f)の鋭さで決まることから、その値が評価指標として使われます。この値をQ値と言います。以上から、SRRの設計には十分大きなQ値を持たせることが大切です。
３．メタマテリアルの応用例（用途）
次に、メタマテリアルの主な応用例について簡単にご紹介します。
（1）完全レンズ
通常、物体に光を当ててレンズによって像を作ると、像の分解能は光波長の制限を受けてしまいます（回折限界）。つまり、物体の像には光波長よりも細かい構造が反映されません。
しかし、負の屈折率からなる「完全レンズ」を使用すると、微細な構造までも結像させることが可能になります（図8）。
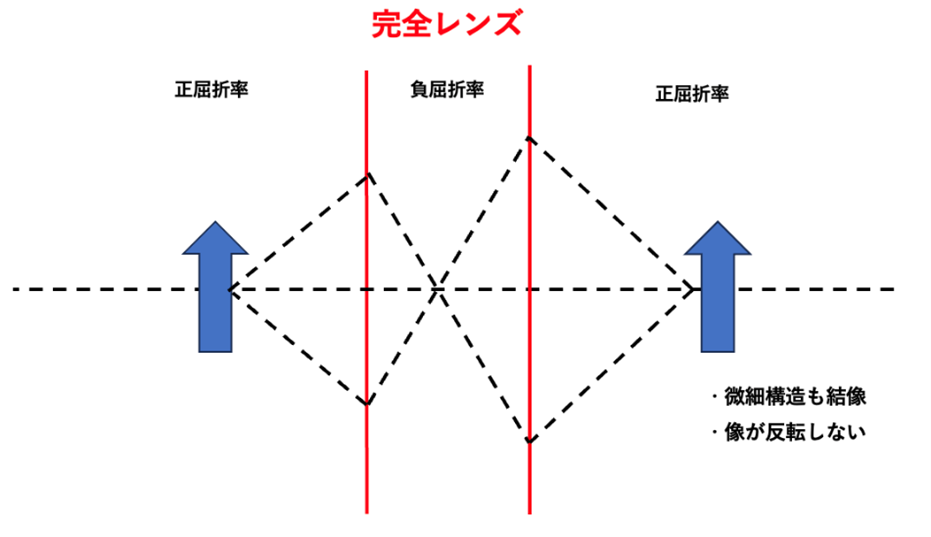
【図8 完全レンズのイメージ】
（2）光学迷彩（透明マント）
人が物体を認識するのは、光が物体に当たった反射光が目に入る、あるいは物体によって光が遮断されたときになります。
これらの要因を排除すれば、物体は人の目で見ることができなくなり透明になります。
それを実現するためには、透明にしたい物体を、メタマテリアルを用いて複雑な屈折率分布を形成した球殻状物体で覆えば良いのです。すると、図9のように人の目には後ろの景色しか見えなくなります。
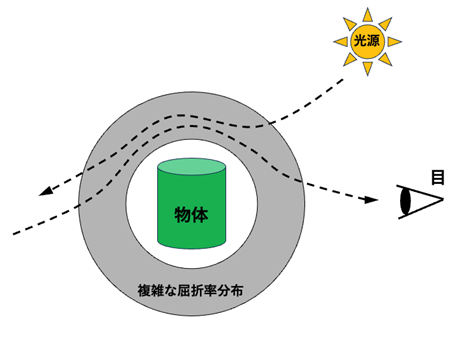
【図9 物体が透明になるイメージ】
以上、完全レンズや透明マントなど夢のある技術を紹介してきましたが、その他にも多くの応用例が生まれており、メタマテリアルはより身近なものになってきています。
（アイアール技術者教育研究所 Y・F）
【併せて読みたい関連コラム】
《引用文献、参考文献》
- [1] 「メタマテリアルのための光学入門」, 左貝 潤一
- [2] 「光マテリアル入門,」 田中 拓男
- [3] 「電磁メタマテリアルの研究動向、メタマテリアル―左手系材料を中心として― 総合報告」, 石原 照也
https://annex.jsap.or.jp/photonics/kogaku/public/36-10-sougouhoukoku1.pdf - [4] 「磁性体を用いた平面型電磁ノイズ抑制体のメカニズムと設計、特集/IoT時代を支える最新の電磁特性技術,」 室賀 翔, 遠藤 恭, 田中 元志
https://www.jstage.jst.go.jp/article/jiep/21/7/21_635/_pdf
