2024.09.10 2024.10.16

フックの法則とは？公式と考え方、応力・ひずみとの関係等をわかりやすく解説

フックの法則

当連載コラムでは、機械部材に発生する「応力」と「ひずみ」について解説してきました。
応力とひずみには密接な関係があります。

今回は両者の関係を考える上で重要となる弾性変形とフックの法則について簡単に解説します。

１．【前提知識】弾性変形とは？

物体に外力を加えると、物体は変形しますがある限界の大きさの外力以下であれば、外力が解放されてゼロになれば、変形もゼロとなり、物体は元の形（寸法）に戻ります。
このような変形を「弾性変形」（elastic deformation）といいます。

物体に外力が加われば、物体内部には応力とひずみが生じます。
弾性変形においては、外力が加わった後にゼロとなれば、物体内部の応力とひずみもゼロとなります。

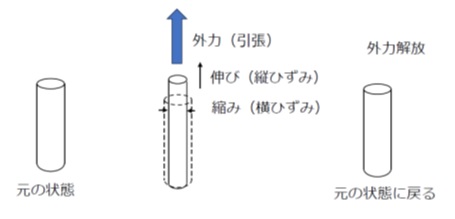
弾性変形とは
【図1　弾性変形】

２．フックの法則とその公式

物体が外力（荷重）を受けて弾性変形するとき、外力の増加とともに物体の変形量も増加します。
多くの材料では、外力がある限界値に達するまでは外力と変形量との間には単純な比例の関係が成立します。
これを「フックの法則」（Hooke’s law）といいます。

フックの法則は、1678年にイギリスの物理学者ロバート・フック（Robert Hooke）によってはじめて提唱された法則であり、弾性変形を扱う際の基礎となります。

外力（荷重）をF、変形量をxとすれば、フックの法則は次式のように表すことができます。

　　　F = kx　　・・・（１）　［フックの法則の公式］

３．ばねの変形とフックの法則《ばね定数とは？》

物体の弾性変形を利用する代表的な機械要素として「ばね」があります。
「ばね」には、「コイルばね」「板ばね」「さらばね」など、様々な種類がありますが、ばねに外力が作用したときのばねの変位x（伸びまたは縮み）と外力Ｆの関係はフックの法則（１）式で表すことができ、比例定数kを「ばね定数」（spring constant）といいます。

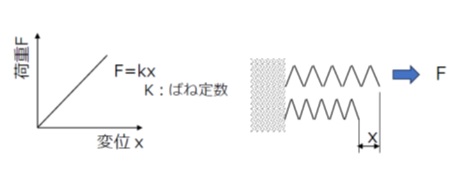
【図2　フックの法則（ばね）】

４．応力、ひずみとフックの法則

物体が外力を受けて変形するとき、物体内部に生じる応力とひずみに着目した場合にも、フックの法則をあてはめて考えることができます。

応力が、物体に使用する材料に固有のある限界値に達するまでは、応力とひずみの間にはフックの法則が成立します。
応力とひずみの比例関係が保持される限界の応力を「比例限度」といい、フックの法則が適用できる比例関係における比例定数をその材料の「弾性係数」（elastic modules）といいます。

垂直荷重を受ける物体の場合、比例限度内では垂直応力σ、縦ひずみε、弾性係数Eの間に（１）式と同様に次式のような関係が成立します。

　　　σ = Eε　　　・・・（２）

Eを「縦弾性係数」または「ヤング率」といいます。

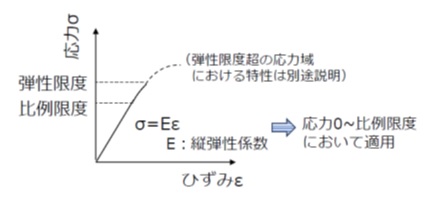
【図3　フックの法則（応力-ひずみ）】