【電気数学をシンプルに】電気回路の解析② 行列の演算方法をチェック《練習問題付》

今回のコラムでは、電気数学で必要となる前提知識のうち、「行列」の計算方法を解説します。
【前提知識】行列の演算について基本を押さえよう
(1)行列の加算 A+B
行列の加算は、対応する成分ごとに計算をします。
図1には対応する成分を色分けして示しています。
各行列のi行j列成分の和aij+ bijが行列の和のi行j列成分になります。
つまり、行列の加算は、行数と列数が等しい行列どうしでなければ計算ができません。
また、その和も、行数と列数が等しくなります。
すなわち、図1のように、3×2行列と3×2行列の和は、3×2行列になります。
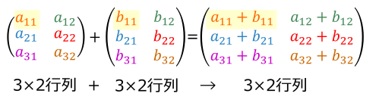
[図1 行列における加算]
なお、同じ行列Aの加算の場合、
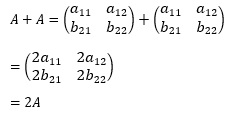
となり、行列のスカラ倍は、各成分のスカラ倍になることがわかります。
(2)行列の減算 A-B
行列の減算も、加算と同様に対応する成分ごとに計算します。
(3)行列の乗算 AB
行列の乗算は、掛けられる行列Aの列数nと、掛ける行列Bの行数nとが等しい場合にのみ定義されます。
例えば、図2に示されるように、2×3行列と3×1行列の積は定義され、その積は2×1行列になります。
掛けられる行列Aのi行成分と掛ける行列Bのj列成分を順に一つずつ掛け算したものの和が、行列の積のi行j列成分になります。行列の積は、一般に可換性がなく、AB≠BAになります。


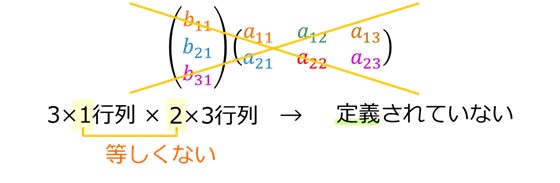
[図2 行列における乗算]
【練習問題】行列の積を求めてみよう
では、実際に行列の積を求めてみましょう。
![]()
これについて、練習問題を3問つくってみました。是非チャレンジしてみてください。
問1
ABとBAを求めよ。
《問1の解答》
《問1の解説》
問2
AOを求めよ。
《問2の解答》
《問2の解説》
問3
AEを求めよ。
《問3の解答》
《問3の解説》
3問とも正解できましたか?
行列の「除算」は・・?
ということで今回は、行列の演算として、加算、減算、乗算について解説しました。
ここで、除算については忘れているわけではありません。行列では除算が定義されていません。
ただし、除算に相当する演算としてイメージできる「逆行列」が定義されています。
次回は、その逆行列について解説しますので、それまでに本コラムの内容をしっかり理解するよう努めていただけたらと思います。
[※電気回路の解析③ 逆行列と行列式はこちら]
(日本アイアール株式会社 N・S)



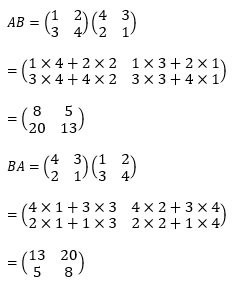
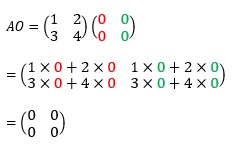
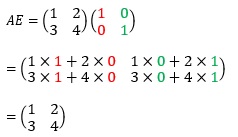







](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)
































