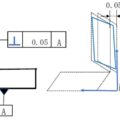
幾何公差入門【提携セミナー】
| 開催日時 | 2024/12/26（木）13:00～17:00 |
|---|---|
| 担当講師 | 北沢 喜一 氏 |
| 開催場所 | Microsoft Teamsによるオンライン受講 |
| 定員 | 8名 |
| 受講費 | 29,700円（税込） |
幾何公差入門
【提携セミナー】
主催：株式会社プラーナー
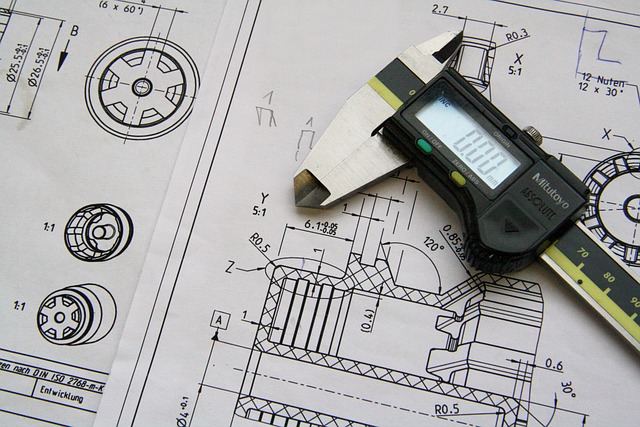
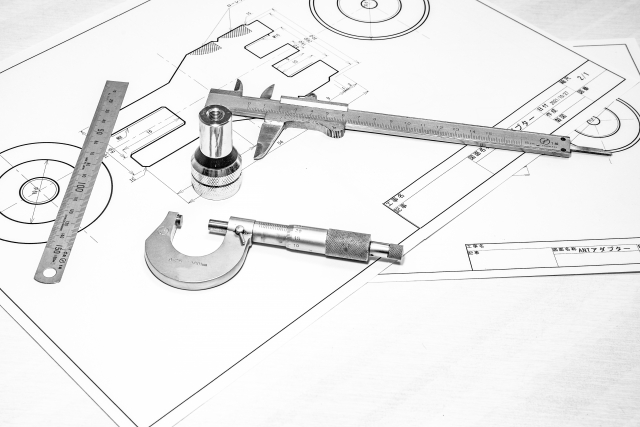
幾何公差は世界的に利用が進んでいますが、いざ使ってみようとなった時、どう使えばいいのかわからなくて悩まれる方が多くいらっしゃいます。
本講座では、幾何公差がなぜ必要となっているのか、幾何公差の基本的な考え方とはどんなものか、幾何公差に欠かせない基準（データム）の考え方、それぞれの公差の公差域など、幾何公差の基本についての知識を習得できます。
主な対象者
- これから幾何公差について学ぶ方
期待される効果
- 幾何公差の必要性、幾何公差の基礎、幾何公差に欠かせない基準（データム）の考え方、公差の公差域の知識を習得できます。
担当講師
北沢 喜一 氏
セミナープログラム（予定）
・ はじめに
どうして幾何公差が求められるのか
幾何公差とはどんなものか
1 幾何公差の用語・種類
1.1 幾何公差の用語
1.2 形体とは
1.3 公差記入枠とは
2 データム
2.1 データムとは
2.2 3平面データム系の構築
2.3 データムの優先順位
2.4 共通データム
2.5 データムターゲット
3 幾何公差図示方法の基本
3.1 公差記入枠とサイズ公差の描き方
3.2 データムの描き方
3.3 幾何公差・データムの図示の基本
3.4 特殊な幾何公差の図示方法
4 形状公差の公差域とその解釈
4.1 真直度
4.2 平面度
4.3 真円度
4.4 円筒度
4.5 線の輪郭度
4.6 面の輪郭度
5 姿勢公差の公差域とその解釈
5.1 直角度
5.2 平行度
5.3 傾斜度
6 位置公差の公差域とその解釈
6.1 位置度
6.2 同心度・同軸度
6.3 対称度
6.4 線の輪郭度
6.5 面の輪郭度
7 振れ公差の公差域とその解釈
7.1 円周振れ
7.2 全振れ
8 より実用的な使い方
8.1 複数幾何公差
8.2 自由状態
8.3 突出公差域
8.4 普通幾何公差
8.5 サイズ公差と幾何公差の関連性
9 各幾何公差の注意点
・ 付録: 最大実体公差方式
・ 最大実体公差方式の用語
・ 最大実体公差方式の考え方
・ 最大実体公差方式のメリット
・ 最大実体公差方式の説明・適用
公開セミナーの次回開催予定
開催日
2024年12月26日（木）13:00～17:00 （適宜休憩時間あり）
開催場所
Microsoft Teamsによるオンライン受講
受講料
29,700円（税込）
配布資料
電子テキスト
お客様の決済後に登録メールへ電子テキストにアクセスする接続URL、ログインID、パスワードをセミナー前に送付します。
備考
ご準備いただくもの
- PC（※インターネットに常時接続可能な環境が必須です。）
- 関数電卓
- 筆記用具
お申し込み方法
★下のセミナー参加申込ボタンより、必要事項をご記入の上お申し込みください。
※このセミナーのお申込期限は、セミナー開催日の1週間前となります。ご了承ください。
おすすめのセミナー情報
注目のセミナー
不具合未然防止の基本と実務への適用《事例で学ぶ FMEA/FTA/DRBFMの効果的な使い方》（セミナー）
開催日時 2024/12/3（火）9:30～16:30
《事例で学ぶ》リチウムイオン電池の課題解決と関連ビジネスの成功パターン（セミナー）
開催日時 2024/11/28（木）13:00～17:00
コーティング膜および機能性材料の付着・密着性評価と剥離対策（セミナー）
開催日時 2024/11/29（金）13:00-16:30
やさしい図面の書き方 図面情報編（セミナー）
開催日時 【会場受講・LIVE配信受講】2024/11/29（金）10:00-17:00 【アーカイブ受講】12/3～12/16
LTspiceで学ぶ電子部品の基本特性とSPICEの使いこなし（セミナー）
開催日時 2024/12/5（木）10:00～16:00
機械材料の選定の基礎（セミナー）
開催日時 2024/12/5（木） 10:00-16:30
磁気センサの設計手法および効果的活用法（セミナー）
開催日時 未定
人気のコラム
