QC七つ道具の基本③ 散布図とは?
QC七つ道具とは?
ものづくりの基本的な技法に、QC七つ道具というものがあります。
QCというのは、品質管理=Quality Control のことです。
QC七つ道具は、品質管理のキホン技法ということになります。製造業のあらゆる分野で用いることができる、ものづくりに関わる人にとっては必修の技法となります。
- パレート図
- ヒストグラム
- 散布図
- 特性要因図
- 管理図
- チェックシート
- グラフ(層別)
このような7つの技法を合わせて、QC七つ道具と呼びます。
一つずつみていきましょう。
このページでは、散布図について紹介します。
散布図とは?
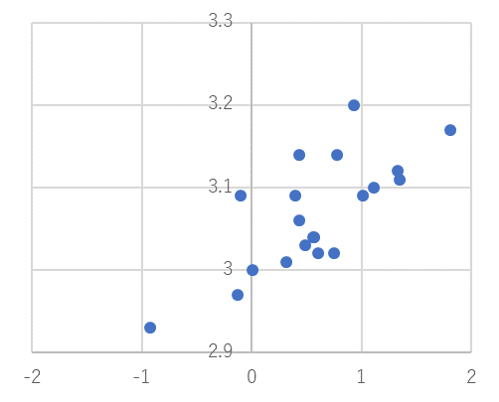
散布図は、横軸と、縦軸に、それぞれの特性値を対応させて、プロットした図です。対象とするデータは、少なくとも2つの特性を持つデータ要素となります。
たとえば、金属板の打ち抜き(ブランキング)加工において、打ち抜いた板の厚みを特性①、打ち抜いた板の反りを特性②、として、各板材(データ要素)の特性①と特性②を2軸にプロットしていきます。
このように散布図を作成すると、特性①(板の厚み)と、特性②(板の反り)との関係性がみえてきます。厚みが厚いほど、反りが大きくなる、という傾向が見えなくもありません。
このように、散布図を作成すると、複数の特性を持つデータ群の、それぞれの特性の関係性や、因果関係を見出すことができます。
散布図は、特性値のばらつきの原因を考えるときに、他の特性値が何らかの関係があるのではないか、という仮説を検証するために用いることができます。
なお、どの特性をどの軸に当てはめるかは自由ですが、原則的に、原因を横軸、結果を縦軸、という当てはめ方のセオリーがあります。数学のxy座標でも、与えたx(横軸)に対して、y(縦軸)が求められる、という関係になるのと同様です。
相関係数
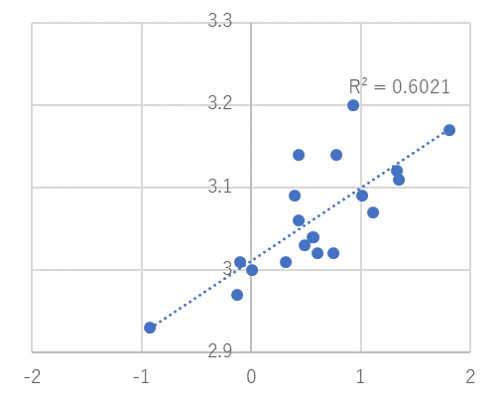
特性①と特性②の関係性を示す指標が、相関係数というものです。相関係数が1になると、すべてのデータは右上がりの直線上にあることになり、完全な相関関係を示すことになり明日。相関係数が0の場合は、無相関、つまり関係性がないということになります。なお、右下がりの傾向の場合は相関係数はマイナスの値となります。つまり相関係数は1-~+1の範囲の値をとることになります。Excelの散布図では、近似曲線を示して、そのR二乗値(相関係数の二乗値)を示すことができます。
散布図の作成方法
散布図は、Excelのグラフ作成ツールで簡単に作成できます。
特性①と特性②を持ったデータ群を準備して、データを選択してグラフの挿入を行います。
散布図活用の注意点① データの数
相関係数と、相関の強さは、当然関係がありますが、必ずしも相関係数の値=相関の強さとはいえません。一般には、相関係数の二乗(R二乗値)が0.5以上あると、多少なりとも相関関係がある、というような判断をすることが多いですが、必ずしも正しいとはいえません。その理由は、相関係数の信頼度はデータの個数に依存するためです。
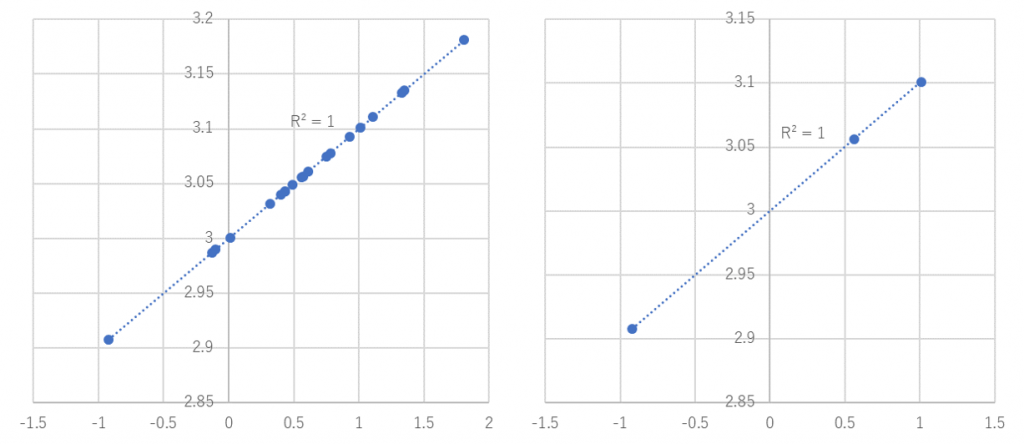
例えば、3点のデータ一直線上に並んだ場合と、100個のデータが直線状に並んだ場合とで、ともに相関係数は1(または-1)となりますが、後者の方が相関係数の信頼度は高くなります。
仮に、本当は相関関係がない特性①と特性②が、たまたま一直線上に並ぶ可能性を考えると、3点のデータではたまたま一直線に並ぶ可能性が考えられますが、100点のデータが偶然一直線上に並ぶことは極めて考えにくい、といえます。
一般に、データは50点程度あると、相関係数の値は十分信頼できる、という判断ができます。もちろん、実務において十分なデータ数を集めることが困難な場合もありますので、その場合は、データの数が少ないことを考慮したうえで結果を扱う必要があります。また、データを層別した場合に、それぞれの項目のデータ個数で考えなくてはならない点も注意が必要です。
散布図活用の注意点② 特性の関係性について
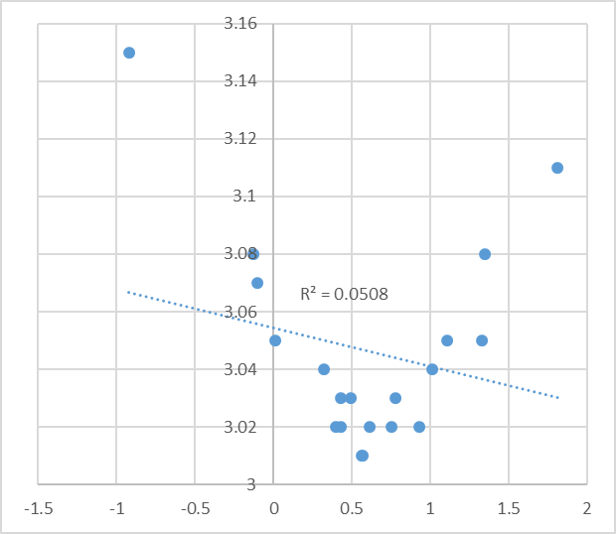
もう一つの注意点として、特性どうしの因果関係を考えるときに、必ずしも散布図にした場合の直線になるとは限らないという点があります。散布図で示す相関係数は、直線に近いかどうかで決まります。実際に、特性どうしの因果関係は、直線ではなく、曲線の関係性もあり得ます。その場合に、散布図の相関係数だけでは議論できないということになります。下の図の例では、明らかに特性①(横軸)と特性②(縦軸)に関係性があるように思われますが、R二乗値は0.05(相関係数0.23)と低い値となっています。これは関係性が直線関係でないためです。
散布図活用の注意点③ 相関関係と因果関係について
散布図の活用により、特性同士の関係性を見出すことは大変有意義な取り組みですが、因果関係について、どう判断するかは注意が必要です。
散布図で見いだされる因果関係とは、原因である特性①によって、結果である特性②が決定される、という関係性のことです。特性②の値を変化させる要因が特性①の中にある、と考えることになります。しかし、特性同士の相関関係が確認された場合に、それが因果関係を示すものであると単純にいうことはできないことに注意が必要です。
原因となる要素は、他にあり、特性①も特性②も、その要素によって支配されている、という可能性があります。また、特性①が原因で特性②が結果だ、と考えていたのが、実は逆だった、ということもありえます。
散布図では、2つの要素の関係性を視覚的に明確化することができますが、なぜそれが影響するのか、という因果関係を説明しうるものではありません。技術において、原因やメカニズムを追究する上では、その技術の理屈に沿った形の仮説やモデルを立てて、その実証として、散布図や相関の分析を行う、という形が望ましく、その逆の順序になってしまう場合は注意が必要です。
(アイアール技術者教育研究所 K・O)
関連コラム:「QC7つ道具の基本」シリーズ