【早わかりポンプ】実揚程、全揚程そしてシステムヘッド

Tweet

Pocket

今回は、当連載中で既に何度か登場している「実揚程」「全揚程」「システムヘッド」の説明です。
特に実揚程と全揚程の違いについて、詳しく解説したいと思います。

１．実揚程について

ポンプが設置される系統において、ポンプが液体に実際に付与する位置エネルギー（ヘッド）のことです。

図１の様な系統があるとします。

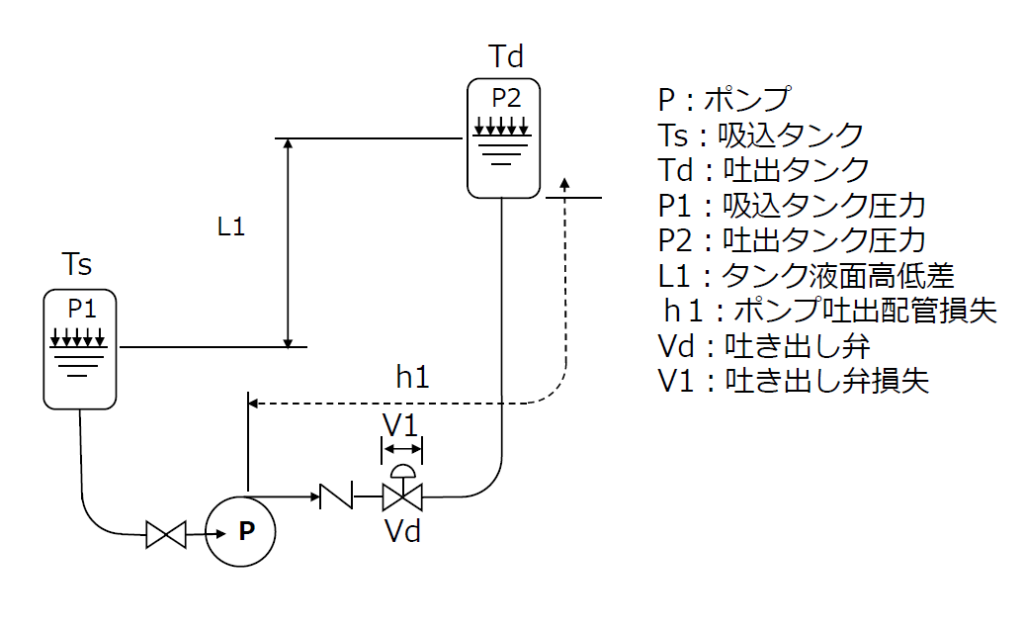
［図1：送水系統図の例 ①］

 
この系統でポンプが液に与えるべきエネルギーには次の2つがあります。

1. 圧力差：低圧の吸込みタンクから高圧の吐出しタンクへ液を送るので、圧力差P2-P1に相当するエネルギーが必要となります。
2. 高低差：低所の吸込みタンクから高所の吐出しタンクへ液を送るので、液面高低差L1に相当するエネルギーが必要となります。

実揚程とは？

ポンプが液に与える実エネルギーを「実揚程」と呼びます。
システム（ポンプ設置系統）側から見れば、揚水（送水）するために必要な位置エネルギー差のことです。
実揚程は、位置エネルギーに換算（ヘッド換算）した圧力差と液面高低差の合計となります。

液体の密度を ρ(kg/m³)、重力加速度を g(m/s²) とすると、ヘッド換算圧力差Ha1は次の式で求めることができます。

　Ha1=P2x10⁶/ρg-P1x10⁶/ρg(m)　・・・（1）

式(1)は、圧力を深さ（液柱の高さ）に換算することを意味します。

《実揚程の計算例》

例えば、水槽に張られた水の深さが10.2(m)で、水の密度ρ=1000(kg/m³)であるとします。
重力加速度をg=9.8(m/s²)とすれば、水槽の底に作用する圧力Pは、
　P=Hxρx g/10⁶ =10.2x1000x9.8/10⁶ =0.1MPa

つまり、密度1000(kg/m³)の水を扱う系統があって、ポンプ吐出し槽と吸込み槽の圧力差が0.1MPaであれば、これに相当するヘッドは10.2mということになります。

圧力差が同じ0.1MPaでも、扱う液体が例えば密度800(kg/m³)の油であるとすれば、これに相当するヘッドHは
　H=0.1×10⁶/(800×9.8)=12.75m
になり、実揚程は水の場合よりも大きな値となります。

つまり、圧力差が同じであっても、密度が小さい液の場合には必要な実揚程が大きくなります。

このように、圧力差を液面高差と同じ長さの単位を持つヘッドに換算することで、ポンプに要求される仕様を「実揚程」という共通の指標で論じることが可能になるわけです。

実揚程Haは、Ha1とL1の合計になるので、
　Ha=L1+Ha1(m)　・・・（2）
となります。

（例）
P1=0.1MPa, P2=0.2MPa, ρ=850kg/m³, g=9.8 m/s², L1=18m であるとき
（1）,（2）式より、実揚程Ha=30 m

２．全揚程について

（1）配管損失

ある流量の液体を、配管系統を通じて流せば、そこには必ず圧力損失が生じます。
これを配管損失水頭と呼びます。

配管損失水頭⊿hは次の式で計算することができます。

　⊿h=(λL/D+Σζi+ζv+1)V²/2g (m)　・・・（3）

　λ：直管の管摩擦係数
　L：直管長さ
　D：配管内径
　Σζi：エルボなどの配管要素の損失係数の合計）
　ζv：吐出し流量調整弁の損失係数
　v：配管流速 (m/s)
　1の意味：最終吐出しに必要な速度エネルギー(*注1)

(*注1)つまり配管損失を消費してなお、吐出し槽内に流速Vで流体を送り出すためのエネルギーを残しておくことが必要になります。吐出し形態が単なる吐出し口ではなくて、例えば消火ノズルのように抵抗（絞り）要素を持つ場合は、１ではなくその吐出し要素固有の抵抗係数（損失係数）で置き換える必要があります。
 

《全揚程の計算例》

図2のような送水系統があるとします。

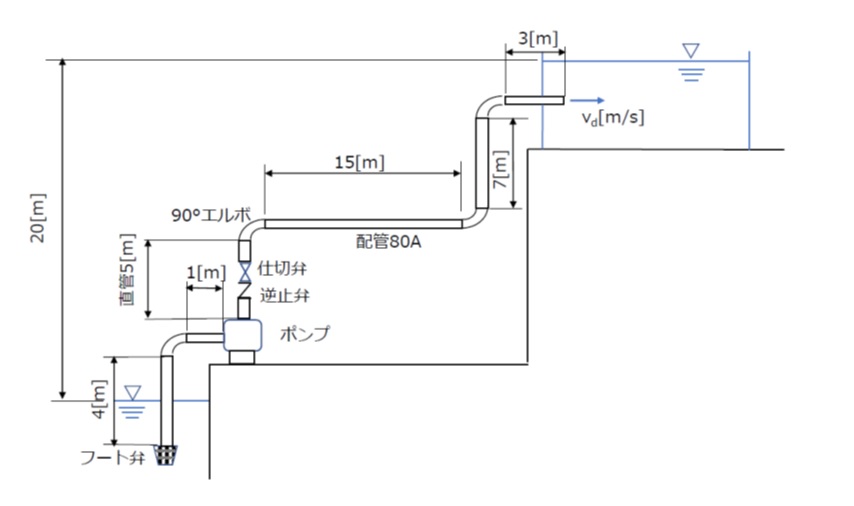
［図2：送水系統の例 ②］

配管口径は吸込み・吐出し共に80Aで内径d=80.7[mm]とします。

流量Q=1.0[m³/min]とすれば、
流速V=1.0/60/{(π/4)0.0807²}=3.26[m/s] 直管全長L=4+1+5+15+7+3=35[m]

管摩擦係数λは、配管の材質や内面粗さと流れのレイノルズ数により変化します。
ここではλを0.03とすると(*注2)、
直管の損失係数 λL/d=0.03×35/0.0807=13.01
一般的な資料より、90°エルボの損失係数0.21

図2の系統では、エルボを4個使用しているので Σζi=0.21×4=0.84

一般的な資料より、弁の損失係数を仕切弁（全開）0.18、逆止弁1.5、フート弁2.0とすれば、
弁類の損失係数 ζv=0.18+1.5+2.0=3.68

よって、式（3）より
⊿h=(13.01+0.84+3.68+1)x3.26²/(2×9.8)=10.0[m]

吸込み、吐出し共に大気圧が作用するとすれば圧力差はゼロですので、実揚程は吸込み・吐出しの水面高低差のみとなり Ha=20[m]

したがって、ポンプの必要な全揚程 H=Ha+⊿h=20+10=30[m] となります。

(*注2)ポンプ全揚程を決定する際には、配管の経年劣化を考慮して、λにある程度余裕を見込んでおく必要があります。

（2）全揚程とは？

Vを配管流速 (m/s)とするとき配管損失水頭は流速Vの２乗に比例します。
流速Vは流量Qを配管断面積で除した値ですので、配管径が一定であるとき、流速は流量Qに比例します。

したがって、損失水頭は次のように表すことができます。

　配管損失 h1=A₁xQ²　・・・（4）　
　吐出し弁損失 V1=A₂xQ²　・・・（5）

（※A₁,A₂：流速を流量に置き換えたときの配管および吐出弁の損失係数）

ポンプが流量Qの液体を、配管系統上の所定の位置まで送る（実揚程を付与する）ためには、実揚程Haに加えて配管損失水頭に相当するエネルギーを液体に与える必要があります。
すなわち、全揚程は実揚程と配管損失（弁を含む）の合計のことを指します。

　A₁+A₂=Aとおけば、式(2),(4),(5)より
　全揚程H=Ha+AQ²　・・・（6）

（3）システムヘッド

上記の（6）式からわかるように、実揚程は流量によらない定数、配管損失は流量の2乗に比例する関数となります。
横軸に流量、縦軸に全揚程をとって表すポンプQHカーブに、配管損失を重ねて表示すると、縦軸上の実揚程に相当する点を起点とする二次曲線として表されます。
これを「システムヘッドカーブ」といいます。

ポンプの運転点は、QHカーブとシステムヘッドカーブの交点となります。

例えば
　Q=50, A=0.008（システムヘッド1),Ha=30のとき、H=50
　Q=50, A=0.012（システムヘッド2),Ha=20のとき、H=50
とすると、両者ともポンプ要項はQ=50,H=50となりますが、実揚程とシステムヘッドが異なります。

これをポンプ特性（QH曲線）と重ねてみると図3のようになります。
 

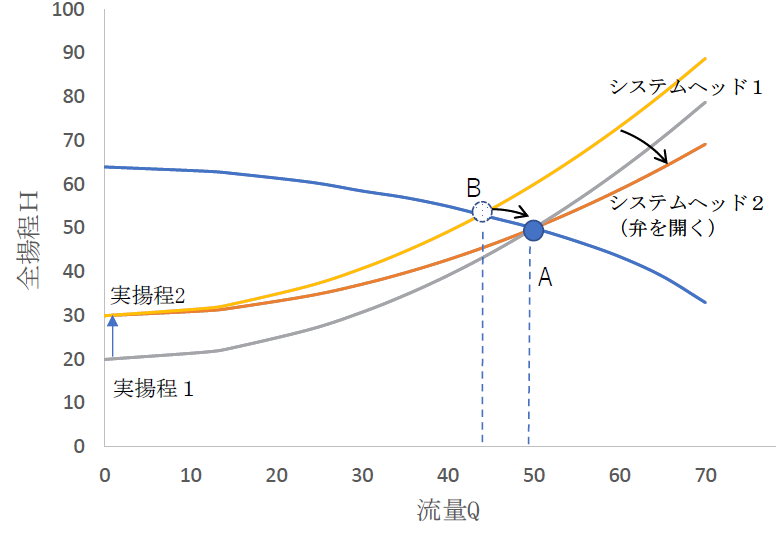
［図3：QHカーブとシステムヘッド］

• システムヘッド1の場合：実揚程は低いが配管損失が大きい
• システムヘッド2の場合：実揚程は高いが配管損失が小さい

ある実揚程を得るためには、弁を含む配管損失（システムヘッド）に打ち勝って流量Qを送るために必要な揚程（ヘッド）を加える必要があるので、ポンプ要項は、実揚程ではなく全揚程で表示します。

また、実揚程は流量には依存しませんが、季節あるいはシステム負荷などの要因によっては変動することもあります。（水位差、貯槽の圧力変化など）

実揚程が大きくなって、システムヘッド特性が同じであれば、ポンプ流量は小さくなります。（図2のA点からB点へ移行）
この場合は、弁開度を大きくしてシステム抵抗を下げ、元の流量点Aが再び得られるようにします。（システムヘッド1から2へ）

《吐出し弁と流量制御》

配管損失計算例の図2の系統では、実揚程20[m]のときに、吐出し弁を全開にして規定の流量を得られるように計画すると、吐出し水位が上昇して実揚程が当初の20[m]より大きくなったとき（図3の実揚程1から2に相当）、吐出し弁を開く余地がないので規定流量へ回復させることができません。

吐出し弁以外に流量調整手段がなく（回転速度一定）、将来的に実揚程が上昇する可能性がある場合は、当初の実揚程に対して、ある程度吐出し弁を閉めて規定流量が得られるように計画する必要があります。

図2では計算例として吐出し弁を仕切弁（全開）としました。
仕切弁は開度を絞ったときの流量調整機能が良くないので、弁開度で流量調整する場合は、仕切弁ではなく玉形弁とする必要があります。ただし、玉型弁は全開時でも仕切弁に比べると損失が大きいので注意が必要です。
 

（４）実揚程の高低と回転速度制御

当連載コラムの「ポンプの効率と省エネ化」の回で、ポンプを可変速仕様とすることにより、吐出し弁で流量調整する場合と比較して省エネ効果が大きいことを書きました。
回転速度の許容変化幅は、実揚程とシステムヘッド特性で大きく変わります。

たとえば図4のように空調用に用いる循環ポンプは、閉ループ配管系統の間を水が循環して戻ってくるので実揚程は小さく（冷却塔の落差程度）、熱交換器など機器を含む配管損失が大半を占めます。
このような場合は、回転速度の許容変化幅が大きくなり、図の例では40％速度でも運転が可能です。

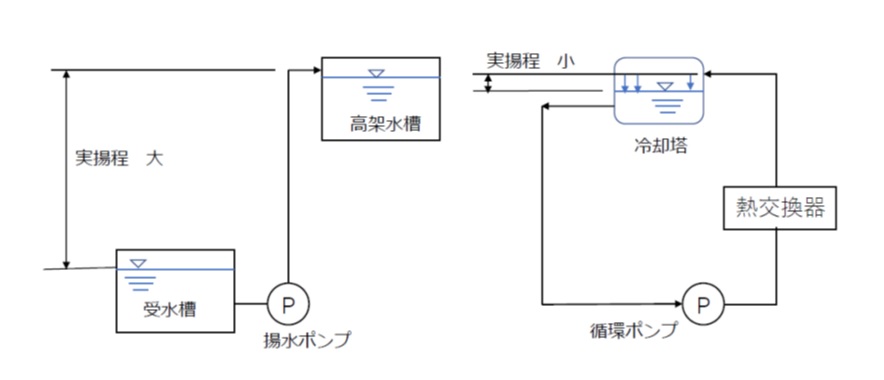
［図4：用途による実揚程の大小の例］

一方、高架水槽など高い所に水を送水する場合は、配管抵抗よりも実揚程が占める割合が大きくなります。
図5の場合、60％速度ではQHカーブがシステムヘッドを下回るので揚水ポンプとしては運転することができません。可変速仕様を導入する場合には、ポンプQHカーブとシステムヘッドの関係から運転可能最低回転速度を確認することが重要です。

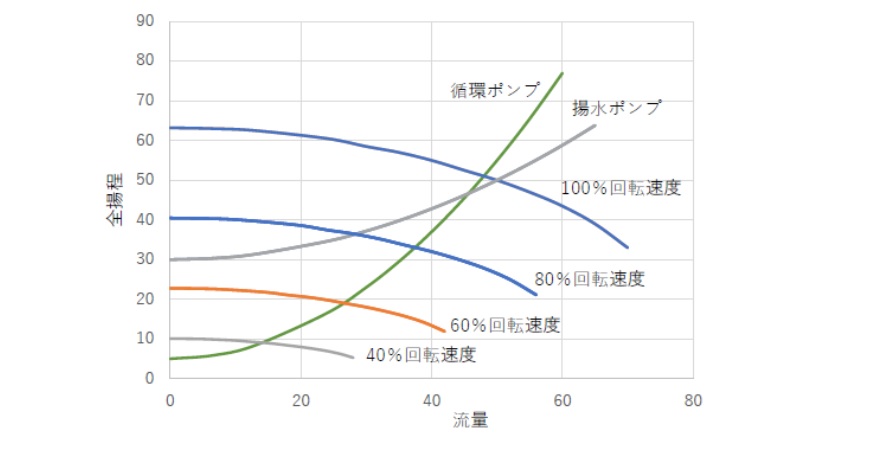
［図5：実揚程・システムヘッドと回転速度制御］

（5）ポンプ全揚程の測定

工場における性能試験で、あるいは現地で、ポンプの全揚程を直接測定することはできません。
ポンプの吸込み・吐出しに設置した圧力計の測定値から全揚程を換算することになります。

このとき、圧力計で測定されるのは静圧で、一方、全揚程は静圧と動圧の和すなわち全圧をヘッドで表した値であることに注意する必要があります。
また、吸込み・吐出しの圧力計設置高さが、ポンプ基準高と異なる場合には、位置エネルギー差の補正が必要となります。

吐出し圧力計の指示値をPd[kPa]、吸込み圧力計の指示値をPs[kPa]、吐出し流速をVd[m/s]、吸込み流速をVs[m/s]、吐出し・吸込み圧力の測定点高差をhm[m]とすれば、ポンプ全揚程H[m]は次式のようになります。

　H=(Pd-Ps) x10³/ρg+(Vd²-Vs²)/2g+hm　・・・（7）
 

例として、下図の系統で全揚程を計算してみましょう。

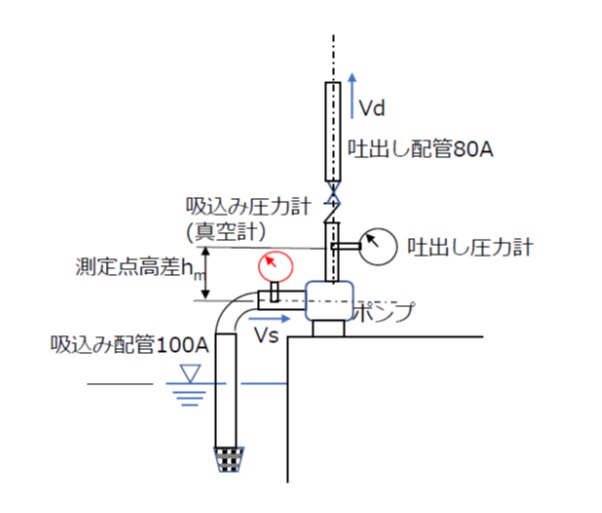
［図6：ポンプ全揚程の測定（例）］

図6の吸込み配管100A(内径105.3[mm])、吐出し配管80A(内径80.7[mm])の系統で、
ポンプ流量Q=1.2[m³/min]、ポンプ軸心と同じ高さに設置した吸込み真空計の指示値が-30[kPa]、ポンプ軸心より0.3[m]高い位置に設置した吐出し圧力計の指示値が200[kPa]、であったとします。

吐出し流速 Vd=1.2/60/{(π/4)0.0807²}=3.91[m/s]　
吸込み流速 Vs=1.2/60/{(π/4)0.1053²}=2.30[m/s]

式（7）より、全揚程Hは次のようになります。
（ただし、水の密度ρ=1000(kg/m³)、重力加速度g=9.8(m/s²)としています。）

　H=(200-(-30)) x10³/ρg+(3.91²-2.3²)/2g+0.3=24.3[m]

このように、ポンプを論じる或いはポンプ購入仕様書を作成する際には、実揚程と全揚程を明確に区別して、ポンプQHカーブとシステムヘッドの関係、およびポンプ運転点の決定方法について理解する必要があります。
 

（日本アイアール株式会社　特許調査部　S・Y)

Tweet

Pocket