断面二次モーメントを徹底解説!基本概念から求め方・計算例までわかりやすく説明

「断面二次モーメント」は、構造物の断面の特性を表す量です。
なぜ、断面二次モーメントは曲げ剛性に関係しているのでしょうか?
計算式で検証することで、断面二次モーメントについて理解していきましょう。
目次
1.曲げ剛性と材質および断面形状の関係
材料力学でよく言われる「曲げ剛性(≒曲げにくさ)が強い・弱い」というのは、具体的には何が原因なのでしょうか?曲げにくさの原因として以下の二つが考えられます。
(1)材質による曲げにくさの相違
片持ち梁を例として、図1に示すように、同じ断面形状のゴムと金属では、やわらかいゴムの方が変形しやすく、硬い金属の方が変形しにくいです。つまり、金属はゴムより曲げ剛性が強いと感覚的にわかります。
これはフックの法則より、同じ断面形状の場合、金属の方がゴムよりもヤング率(材質固有の値)が高いと考えられるためです。
フックの法則によると、部材内に生じる力と変形の間には比例関係が成立します。
σ = E・ε ・・・式1(フックの法則)
ここで、σは応力、εは「ひずみ」(= 変形量 / 元の長さ)、E はヤング係数です。
ε(ひずみ)= 変形量 / 元の長さ ・・・式2
[※関連記事:ひずみとは? 縦ひずみ/横ひずみ、せん断ひずみの求め方、式・記号などを解説 ]
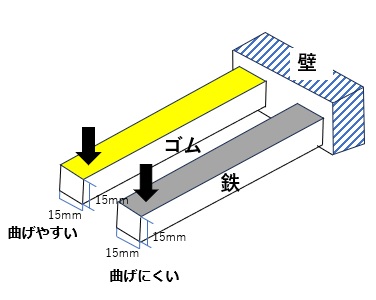
【図1 材質による曲げにくさの相違】
(2)断面形状による剛性(曲げにくさ)の相違
同じ材質(例えば同じ材質の鉄)であっても、図2左図に示すように断面面積が異なれば、曲げにくさは異なります。
一方、同じ材料(例えば鉄)・同じ断面積(15mm×5mm)の角棒であっても、図2右図に示すように、曲げの中心軸(図のy軸)に対する断面形状が異なれば、曲げにくさは異なります。つまり、曲げにくさは断面積だけでは決定できず、曲げの中心軸に対する形状の影響を強く受けることがわかります。
この指標となるのが「断面二次モーメント」なのです。

【図2 断面形状による剛性(曲げにくさ)の相違】
2.断面二次モーメントとは
図3に示すような図形の重心(図心G)を原点とする直角座標系 (y,z) を考えます。
赤色で示す微小面積要素dAと、dAのy軸から距離をzとします。
y軸に関する断面二次モーメントIyは次式で求められます。(一般に断面二次モーメントはIを使用しています)
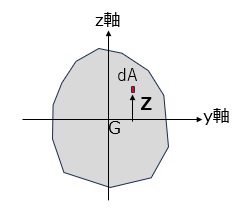
【図3 部材の断面の断面二次モーメント】
![]()
この積分の意味は、断面上のすべての位置について “z2” を足し合わせていく(全断面Aに対して積分する)ということです。
この式から、「断面二次モーメント」とは、曲げの中心軸であるy軸からz方向にどれだけ離れたところに微小面積要素dAが存在するかを表しているということを意味しています。
したがって、y軸に関する断面二次モーメントは、y軸に対し縦方向(z方向)に拡がった形になる方が、断面二次モーメントを大きくする効果が大きいです。一方、z軸に対し、横方向(y方向)への断面の拡がりは、あまり断面二次モーメントには効かないことも意味します。
断面二次モーメントの求め方(計算例)
図4左に示す横方向(y方向)に拡がった断面の長方形断面①について、y軸に関する断面二次モーメントを導出してみましょう。
長方形の図心Gを通り、各辺に平行な座標系を考えると、y軸から距離Zの位置にある微小要素の面積は、次式で求められます。
dA = H × dz
そしてy軸からdAまでの距離zを2乗したものを乗じて、断面の縦寸法に亘って積分します。この場合-B/2~+B/2の範囲となります。(以下の式はこれを表したものです)
![]()
次に、図4右に示す縦方向(z方向)に拡がった断面の長方形断面のy軸に関する断面①の二次モーメントを求めてみましょう。
長方形の図心Gを通り,各辺に平行な座標系を考えると、y軸から距離Zの位置にある微小要素の面積は次式で求められます。
dA = B × dz
そしてy軸からdAまでの距離zを2乗したものを乗じて、断面の縦寸法に亘って積分します。この場合-H/2~+H/2の範囲となります。(以下の式はこれを表したものです)
![]()
H>Bのため、断面②の断面二次モーメントBH3/12の方が、断面①の断面二次モーメントHB3/12より大きいことがわかります。
今度は、材質が同じ断面①・断面②について、どちらの方が剛性が強いか考えてみましょう。
下図のように、断面②のほうが曲げにくい(剛性が強い)ことが感覚的にわかります。つまり、材質が同じの場合、断面二次モーメントが高いと剛性は強いということです。
なぜこのような結果になるのかを、以下で説明します。
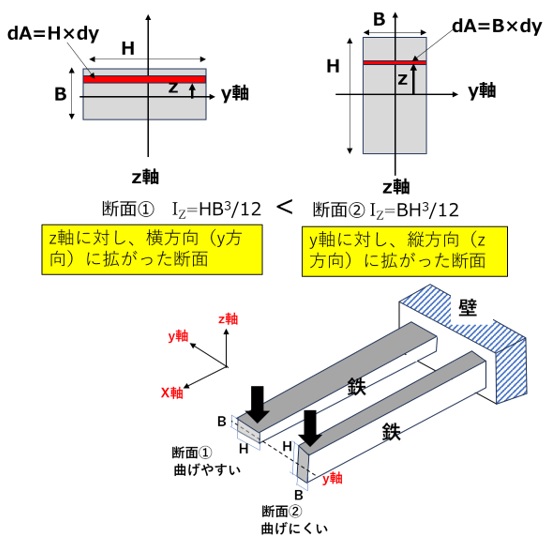
【図4 断面二次モーメントの計算例】
3.曲げモーメントより発生する応力
(1)断面上に作用する応力
図5に示すように、右端に横荷重(曲げの力F)が作用する長さℓの片持梁に作用する応力について考えます。
曲げの力Fにより点Bに生じる曲げモーメントはF(ℓ-x)となります。
つまり、曲げモーメントはx=0のA点で最大となりF・ℓとなり、x=ℓの先端では0になります。
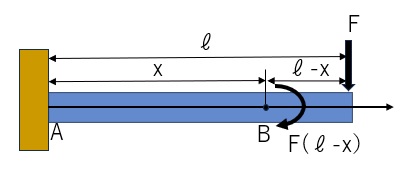
【図5 片持梁】
ここで、梁の任意の位置x=x1微小距離dxにおける断面上に作用する応力について考えます。
図6Aに示すように、曲げの力Fにより、点線で示すように梁はたわみます。図6Bで示すように、微小距離dxにおける断面の図心を通る中立面をx軸とし、中立面の曲率半径をRとします。
中立面より上側で引張応力、下側で圧縮応力が発生します。中立面上の位置では、応力が0になります。また、中立面から離れるに従い大きくなり、上外表面h1、下外表面h2で最大となります。
図1で示した鉄とゴムの比較でもわかるように、同じ曲げモーメントに対し曲率半径Rが大きい場合は、曲げにくいことになります。逆に、同じ曲げモーメントで、曲率半径Rが小さい場合は、曲げやすいことになります。
ここで、断面の応力を詳細に検討してみます。
図6Bに示すように、引張応力により中立面aa面が、bb面に変形したことになります。
式2: ε(ひずみ) = 変形量 / 元の長さ より、
ε=【(R+Z)dθ- dx】/dx =Z/R ・・・式4
(∵ dx=Rdθ ,dθとはdx 離れた2面のなす角度)
フックの法則(式1)に、式4を代入すると
σ = E・ε = E/R ×Z ・・・式5
式5の意味を検討してみましょう。
曲率半径Rは、xの位置によって変化しますが、微小区間dxでは定数となります。
さらにヤング率Eは定数です。したがって、応力αはZの1次関数になります。
このことからも、中立面Z=0で応力は0となり、上外表面Z=h1、下外表面Z=h2で最大値となります。
[※関連記事:「はり」の基礎知識を解説!SFDとBMD、たわみの計算方法などがわかる ]
(2)応力σによる曲げモーメントMの求め方
図6Cに示すように、y軸から距離Zの応力σによるy軸回りの曲げモーメントを計算してみます。
図6Dに示すように、aa面に作用する応力σによる微小面積dAのy軸回りのモーメントは、Z × σdA(腕の長さ×力)となります。
Z × σdAを全断面について積分したものが、全断面に作用する曲げモーメントMになり、以下の式となります。
![]()
式6に式5を代入すると、
![]()
ここで、式3より式8の関係が成り立ちます。
M = (E × Iy) /R ・・・式8
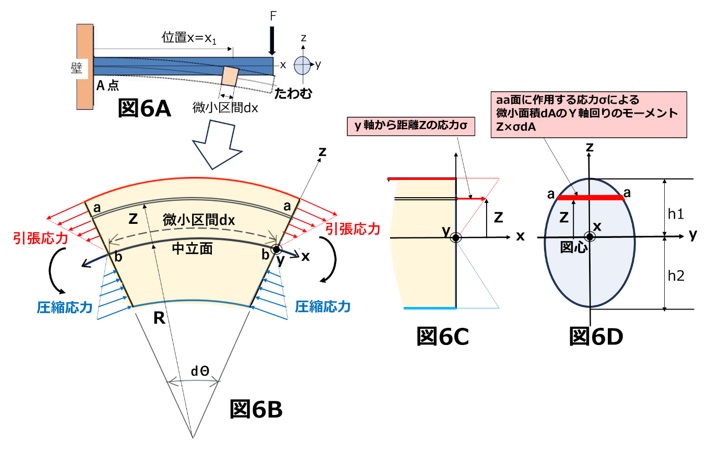
【図6 断面上に作用する応力】
4.計算式による剛性の検証
右端に横荷重(曲げの力F)が作用する長さℓの片持梁に作用する曲げにくさ(剛性)について、前述のように感覚的に判断したことを、式8で検証してみましょう。
(1)材質による曲げにくさの検証
前述しましたように、断面形状が同じの場合、鉄の方がゴムより、曲げにくいのは材料の持つ固有の値であるヤング率が高いためでした。
断面形状が同じの場合は、断面二次モーメントIyが同じことになります。
同じ曲げモーメントMが同じの場合、式8を変形すると、
M/Iy = E/R ・・・式9
式9は、M、Iyが同じの場合、つまり式9の左辺が同じの場合に、式9の右辺はE(ヤング率)が大きいほど、曲率半径Rが大きくなります。
曲率半径が大きいとは、曲げにくいことなので、式9で材質によるヤング率と曲げにくさの検証ができました。
(2)断面形状(断面二次モーメントIv)による剛性の検証
材質が同じの場合、断面二次モーメントIvが高いと剛性は強いことが分かりました。材質が同じの場合は、E(ヤング率)が同じことになります。
曲げモーメントMが同じの場合、式8を変形すると
M/E = Iy/R ・・・式10
式10は、M、Eが同じの場合、つまり式10の左辺が同じの場合に、式10の右辺のIy(断面二次モーメント)が大きいほど、曲率半径Rが大きくなります。「曲率半径が大きい」とは、曲げにくいことなので、式10で断面形状(断面二次モーメント)による剛性(曲げにくさ)の検証ができます。
ということで今回は、断面二次モーメントを理解するための知識と考え方、計算について解説しました。
(アイアール技術者教育研究所 T・I)
《引用文献、参考文献》
- 日本機械学会誌(WEBサイト):やさしい材料力学 第7回 はりの曲げ応力
- 金沢大学:「材料力学 Strength of materials」