【機械設計マスターへの道】カルノーサイクルと逆カルノーサイクル［熱力学の基礎知識④］

Pocket

今回の連載コラムは、熱機関や冷凍機などで行われる作動流体のサイクルについて解説します。

１．熱力学における「サイクル」

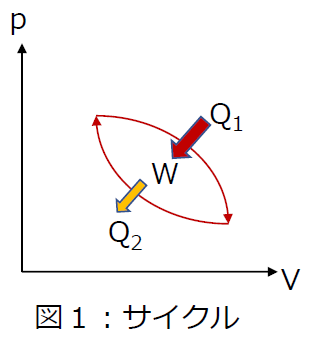
図1のように、作動流体がある経路を通って状態変化し、違う経路をたどって元の状態へ戻るとき、状態変化の経路は閉曲線となります。この変化を繰り返す連続的な循環をサイクルといいます。

熱力学の第2法則によれば、熱機関は高温熱源から熱量Q1を受け取り、外界へ仕事Wをなし、残りの熱量Q2を低温熱源へ放出します。仕事Wが大きいほど熱の有効利用率が高い、つまり効率が良いことになります。

サイクルの熱効率 η=W/Q=(Q1-Q2)/Q1=1-(Q2/Q1)　　　・・・（1）

また図1において閉曲線の上側は、熱源から熱をもらって膨張する過程、下側は圧縮して外部へ仕事をするとともに、低温熱源へ熱を捨てる過程を示します。

したがって、閉曲線で囲まれた面積は1サイクルで行われる有効な仕事量Wを表しています。
閉曲線で囲まれる面積が大きいほど、熱機関の熱効率が大きく、工業的に有用であることを示します。

サイクル

２．カルノーサイクル (Carnot Cycle)

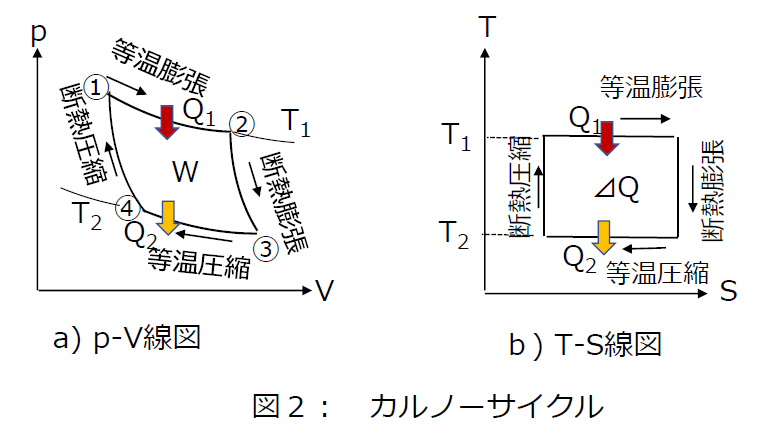
フランスの物理学者カルノーは、熱機関の研究を行い1824年、図2(a)に示すような等温変化と断熱変化で構成されることで、熱効率が最大となる理想的なサイクルが得られることを示しました。
カルノーサイクルは、理想気体を動作流体とし、次の4工程からなる可逆サイクルです。
（※可逆変化は現実には存在しませんが、熱力学では一般に、可逆変化を仮定して状態変化を考えます。）

１）等温膨張（図2の①→②）高熱源温度T1一定で、この間に熱量Q1を受け取る

２）断熱膨張（図2の②→③）膨張して外部へ仕事をなし、温度が低下する

３）等温圧縮（図2の③→④）低熱源温度T2一定で、この間に熱量Q2を捨てる

４）断熱圧縮（図2の④→①）圧縮して温度が上昇し、①の状態に戻る

カルノーサイクル

等温変化と断熱変化からなるカルノーサイクルでは、熱量Qと温度Tの間に次の関係が成り立ちます。

Q2/Q1=T2/T1　　　・・・（2）

したがって（１）、（２）式より、カルノーサイクルの熱効率ηcは

ηc=1-(T2/T1)　　　・・・（3）

カルノーサイクルの熱効率は、高温低温熱源の温度だけで決まります。

なお、完全な断熱や、温度一定など、カルノーサイクル成立条件の実現は困難であり、実際にカルノーサイクルを用いた熱機関を製作することはできません。
あくまで実用的サイクルの効率を比較する際の基準として用いられます。

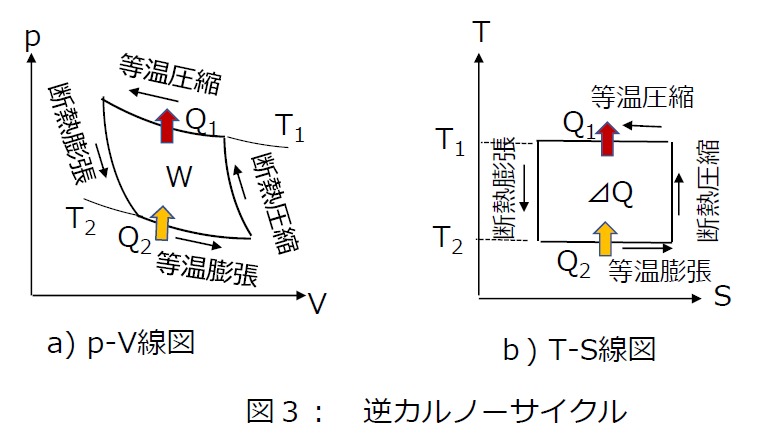
３．逆カルノーサイクル（カルノー冷凍サイクル）

冷凍機やヒートポンプ、エアコンの理想サイクルで、図3(a)のようにカルノーサイクルを逆方向に作動させるものです。

逆サイクルですから外部へ仕事をする代わりに、外部から仕事をもらって、等温膨張する際に低温熱源から熱を受け取り、等温圧縮する際に高温熱源へ熱を放出することができます。作動流体（冷媒）が膨張する際に、シリンダ内部の温度が低温熱源より低下するので熱を取り込むことができます。
このサイクルを回すために外部から与える仕事が消費動力（消費電力）ということになります。

性能指標として熱効率ではなく成績係数(COP)を用います。
COPは消費動力に対してどのくらいの冷房能力あるいは暖房能力を発揮できるか、つまりどのくらいの熱を取り込むことができるかを示すもので、効率と違って1より大きな数字となります。

逆カルノーサイクル