物体まわりの流れパターンとカルマン渦の基本がわかる！ [流体力学の基礎⑥]

流体力学：カルマン渦

物体が流れの中に置かれたり、物体が流体中を動いたりするとき、物体の後方に渦が生じ、物体に力が働きます。航空機、自動車、船舶などの流体中を動く機械を設計するためには、流体中の物体まわりに起きる現象、物体まわりの流れの様相について理解する必要があります。

１．物体まわりの流れと境界層
２．抗力と揚力
- 抗力を減少させている具体例
３．円柱まわりの流れとカルマン渦
- カルマン渦の周波数との共振による事故例
  - ① タコマ橋の崩落
  - ② 高速増力炉「もんじゅ」のナトリウム漏洩

１．物体まわりの流れと境界層

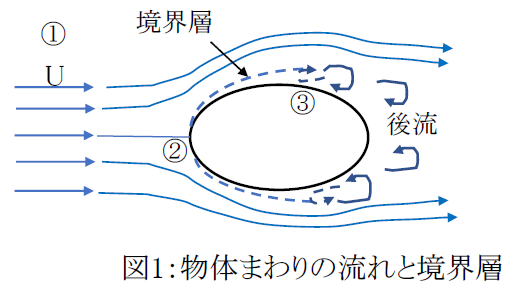
図1に物体まわりの流れの様相を模式的に示します。
物体から十分離れた地点①における流速をUとします。物体前方の点②は流れがせき止められて流速が０となる個所で「よどみ点」といいます。
よどみ点より下流の物体壁面近傍では、粘性力のために減速して速度勾配を有する薄い層が形成されます。これを「境界層」といいます。境界層には流速によって「層流境界層」と「乱流境界層」とがあります。

境界層は、下流に向かうにしたがって厚さが増していき、点③で壁面に沿うことができなくなり、はく離します。はく離点③の下流では、逆流や渦を伴う低圧領域＝後流が形成されます。

物体まわりの流れと境界層

２．抗力と揚力

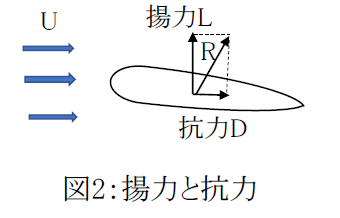
図2のように、物体が相対流速Uで流体中に置かれるとき、物体には力Rが作用します。
Rを流れの方向成分のDと、流れに垂直な方向成分Lに分解したとき、Dを「抗力」、Lを「揚力」といいます。

揚力と抗力

主流中の相対速度をU、流体の密度をρ、物体の代表面積をAとしたとき、抗力、揚力は次式で与えられます。

　抗力D=C_DAρU²/2　　・・・(1)
　揚力L=C_LAρU²/2　　・・・(2)

C_D, C_Lは、それぞれ「抗力係数」「揚力係数」と呼ばれ、実験から求められる無次元数です。

抗力は、流体中を進む物体に対する抵抗となるので、できるだけ抗力を小さくするように設計することが重要です。
抗力には、流れに垂直な方向の「圧力抵抗」と、流れに平行な方向の「摩擦抵抗」とがあります。圧力抵抗を小さくするように工夫された物体形状が「流線形」と呼ばれるものです。
抗力にはこの他に、物体から放出される縦渦による「誘導抵抗」、衝撃波や水面波による「造波抵抗」、複数物体の相互作用による「干渉抵抗」などがあります。

揚力は、航空機や軸流型流体機械の、空力性能・水力性能を向上させるために重要な指標です。
揚力と抗力の比を「揚抗比」といいます。揚抗比が大きいほど、空力・水力性能の向上に寄与（飛行機の燃費が良くなるなど）します。

抗力を減少させている具体例

抗力を減少させる例にゴルフボールのくぼみ（ディンプル）があります。図3を参照ください。

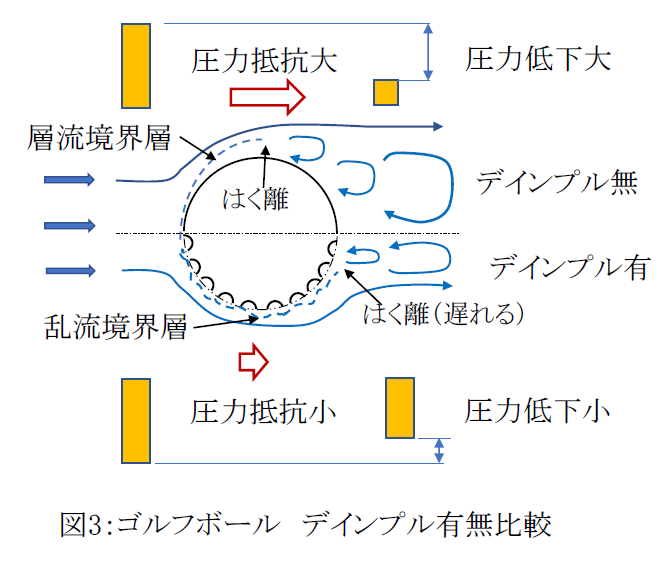
効力を減少させる例（ゴルフボールのディンプル有無比較）

ディンプルのない球状の場合、表面の境界層が層流のまま発達してよどみ点から4分の1周程度の地点ではく離します。はく離点後流には渦が生じて圧力が低下し、上流側との圧力差が大きくなり、圧力抵抗が増えて飛距離が低下します。
そこで、ディンプルを設けることで、境界層が早く乱流境界層に遷移し、境界層のはく離点がディンプルなしの場合よりも後流側になります。そのため、後流側における圧力低下が緩和され、圧力抵抗が減少するので飛距離が伸びます。
表面にくぼみを設けることで摩擦抵抗は増えますが、それ以上に圧力抵抗低減効果が大きいということです。

３．円柱まわりの流れとカルマン渦

断面直径dの円柱が、速度Uの流れに直角に置かれている場合、流体の動粘度をνとしたとき、レイノルズ数 Re=Ud/ν （※レイノルズ数については「管路における圧力損失の考え方と計算」の回を参照）により、円柱後流の流れの様相を分類すると次のようになります。図4を参照ください。

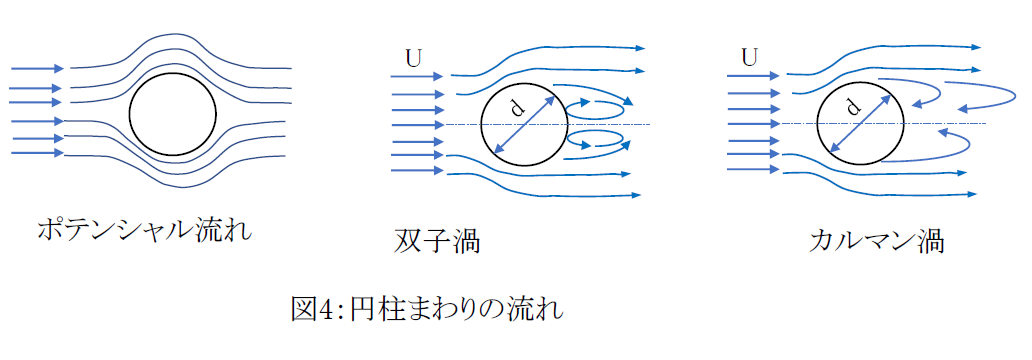
ポテンシャル流、双子渦、カルマン渦

① R_e<5
粘性が支配的で、流れは「ポテンシャル流れ」と呼ばれる、円柱前後でほぼ対称で渦の無い流れとなります。

② 5e<50
円柱背面ではく離が起きて、逆流により回転方向の異なる一対の渦（双子渦）が上下に発生します。

③ 50< R_e (～2×10⁵)
双子渦のような対称性が失われ、渦は交互に放出されて、後流に二列の千鳥状渦列が形成されます。この渦列を「カルマン渦」といいます。
円柱には、周期的な正負の揚力と抗力が発生して、その変動が振動や騒音をもたらします。
冬の風が強い日に、電線がどこかもの悲しい唸り音（もがり笛）を発するのは、カルマン渦の発生によるものです。渦の周波数を f[Hz] とすれば、f とU, d の間には次式の関係があります。

　St=fd/U　　・・・(3)

Stは「ストローハル数」と呼ばれる無次元数で、500< R_e <2x10⁵ の範囲では、ほぼ一定値(St≒0.18)になるため、（3）式を用いて簡単に周波数を求めることができます。

カルマン渦の周波数との共振による事故例

カルマン渦の周波数fが物体の固有振動数と一致すると、共振により重大な損傷が発生する可能性があります。事例を二つ紹介します。

① タコマ橋の崩落

1940年、米国シアトルで橋の完成4か月後に、風速19m/sの風で橋が激しい振動により崩落しました。
橋桁の剛性が低く、ねじれやすい構造であったことに加え、H型鋼を用いた橋桁の端で空気の剥離によるカルマン渦が発生して、橋のねじれ固有振動数と一致したために激しい共振現象を起こして崩壊に至ったものです。

② 高速増力炉「もんじゅ」のナトリウム漏洩

1995年、高速増殖炉「もんじゅ」で、配管の温度検出器取り出し部からナトリウム漏洩が発生しました。
温度計はさや管（ウェル）とよばれる円柱形状の筒に収められて液体ナトリウム中に曝露されますが、後流に発生したカルマン渦の周波数がさや管の固有振動数と一致し、さらにさや管付け根部の形状が不適切で、応力集中によってさや管の付け根部が疲労破壊したものです。
（※応力集中については「強度設計の基礎知識」、疲労破壊については「疲労強度の確認方法と疲労限度線図」の各ページもそれぞれご参照ください。）

このように航空機、自動車、船舶など以外にも、流体（空気、水）中に置かれる機器を設計する際には、空気や水の動き（速度）をよく考慮することが必要です。

（日本アイアール株式会社　特許調査部　S・Y)

≪参考文献≫

・西海孝夫著『図解　はじめて学ぶ　流体の力学』日刊工業新聞社、2010

※本コラムで基礎を概説した流体力学についてさらに深く学びたい方に、おススメの書籍です。

【連載：機械設計マスターへの道】流体力学の基礎シリーズ