【機械設計マスターへの道】主応力とモールの応力円の求め方
当連載「機械設計マスターへの道」の第20回でで三次元応力と破壊学説について説明しました。
今回のコラムでは、その前に基本的に理解しておくべき平面応力の考え方とモールの応力円について、できるだけわかりやすく解説してみたいと思います。
1.平面応力と主応力
例えば図1のような直六面体の二方向に引張り力が作用する状態を考えます。
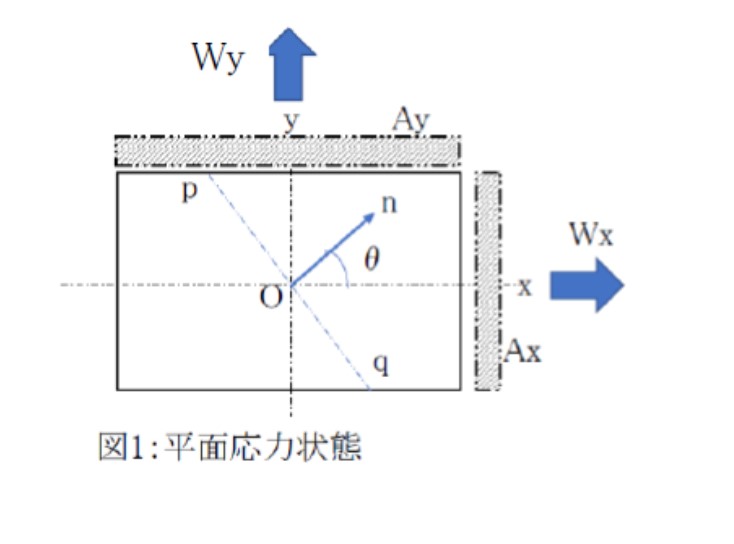
x軸に垂直な断面積をAx、y軸に垂直な断面積をAy、 x軸方向に作用する引張荷重をWx, Y軸方向に作用する引張荷重をWyとします。
次にx軸に対して任意の方向に傾いた断面pqを想定します。断面pqの法線Onがx軸となす角度をθとおけば、断面pqの断面積はAx/cosθです。
Ayとy軸に対して傾いた断面についても同様の考え方を取ることができます。
したがって、荷重WxとWyによって断面pqに生じる垂直応力σとせん断応力τは次のようになります。
σ=Wx/( Ax/cosθ) cosθ+Wy/( Ay/sinθ)sinθ=(Wx/Ax)cos2θ+(Wy/Ay)sin2θ ・・・(1)
τ= Wx/( Ax/cosθ) sinθ-Wy/( Ay/sinθ)cosθ=1/2{(Wx/Ax)-(Wy/Ay)}sin2θ ・・・(2)
(2)式は、三角関数の倍角公式によります。
また、x方向引張荷重Wxとy方向引張荷重Wyによって生じる断面pqのせん断応力は、互いに方向が反対となるため正負の符号となります。
(1)(2)式で、
θ=0[度]のとき σ=Wx/Ax, τ=0
θ=90[度]のときσ=Wy/Ay, τ=0
このように、荷重を受ける物体にはせん断応力がゼロとなる断面が存在し、その断面生じる垂直応力のことを「主応力」と呼びます。また、主応力の最大値を「最大主応力」、最小値を「最小主応力」といいます。
2.モールの応力円
「モールの応力円」は、荷重を受ける物体の任意の方向の断面に生じる垂直応力(引張、圧縮)とせん断応力の大きさを表す円です。
図1の例で、せん断応力 τ=0 となる主応力には、 Wx/Ax と Wy/Ay の2つがあります。
Wx/Ax>Wy/Ay であるとすれば、Wx/Ax=σ1 が最大主応力、Wy/Ay=σ2 が最小主応力となります。
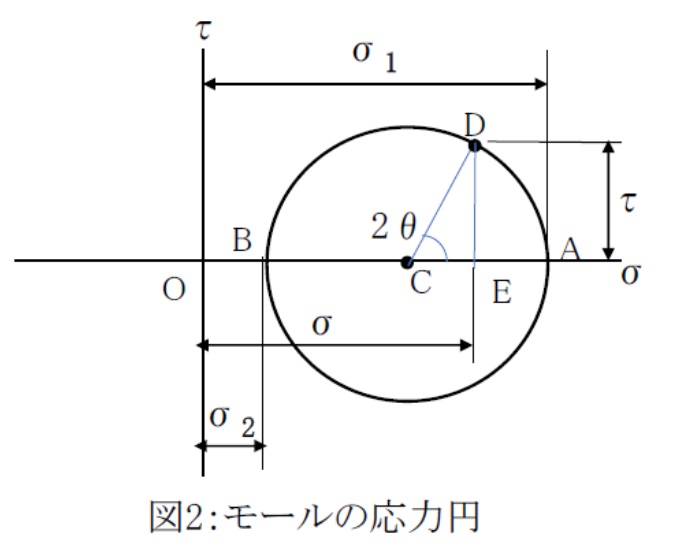
図2のように横軸に垂直応力σ(引張を+、圧縮を-)、縦軸にせん断応力τをとります。
横軸上にσ1とσ2の値をプロットして点A,Bとしたとき、直径ABの円がモールの応力円となります。
この応力円の中心をCとします。
Cを中心に線分CAを、角度2θ回転した応力円上の点Dの横軸座標Eの値は、図1においてx軸から角度θ傾いた方向の垂直応力、Dから横軸に下した垂線DEの縦軸方向値は断面pqのせん断応力を表します。
OE=OC+CE=σ2+(σ1-σ2)/2+1/2(σ1-σ2)cos2θ=1/2(σ1+σ2)+ 1/2(σ1-σ2)cos2θ
=σ1/2(1+cos2θ)+ σ2/2(1-cos2θ)= σ1cos2θ+σ2sin2θ=(1) (倍角公式より)
DE=CDsin2θ=1/2(σ1-σ2)sin2θ=(2)
θ=45のとき、τは最大値となり、その値は ±1/2(σ1-σ2) に等しくなります。
すなわち、互いに直交するx、y軸方向に垂直荷重を受ける物体は、軸に対して45度方向の断面に最大せん断応力が発生します。
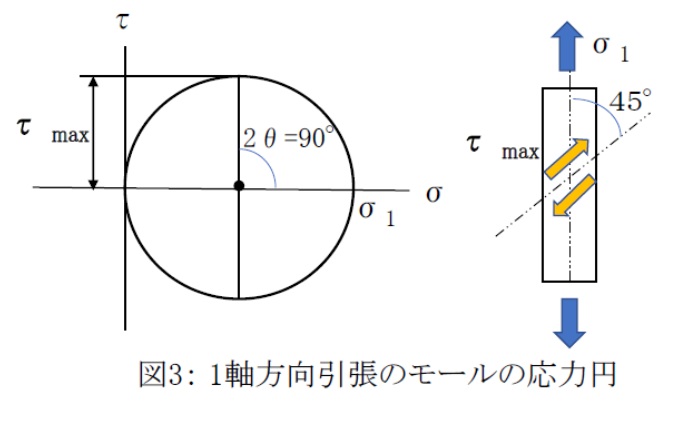
これはWyがゼロの1軸垂直荷重状態でも同じであり、この場合σ2=0ですから、モールの応力円は図3のように、縦軸に接する円になります。
単純引張の場合でも、引張よりせん断に弱い材料特性によっては最大せん断応力が作用する45度方向の断面で破断することがあります。
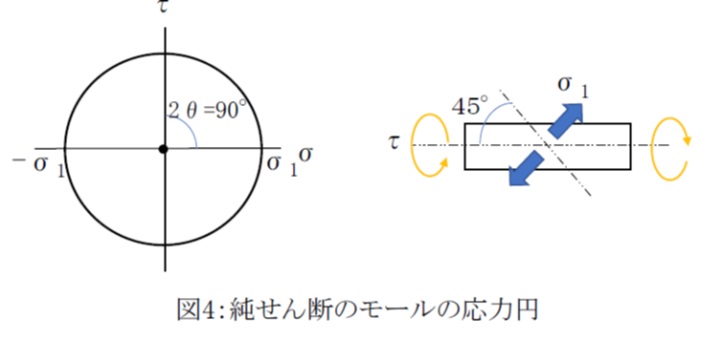
またσ1とσ2の大きさが等しく、σ1が+(引張)、σ2が-(圧縮)の場合には、モールの応力円は図4のように原点を中心とする円となり、垂直荷重方向と45度の角度をなす断面には垂直応力が作用しない純せん断の状態となります。
例えば、丸棒のねじりは純せん断に相当しますが、図4のように45度方向には最大主応力が作用します。
せん断より引張に弱い材料特性によっては、純せん断から45度傾いた面に生じる最大主応力(引張応力)σ1 により破断することがあります。
任意の直交する二方向の垂直応力とせん断応力が与えられたとき、モールの応力円を作図することにより、主応力と主応力面を求めることができます。
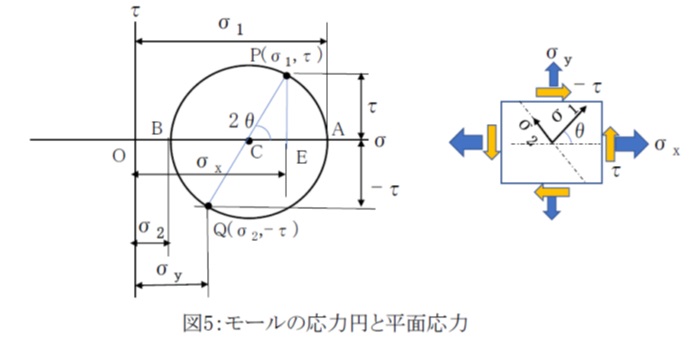
平面応力状態の物体のある表面の応力が σx、σy、τ であったとき、図5のように (σx,τ) の点Pと、(σy,-τ) の点QとをプロットしてPとQを直線で結べば、線分PQと横軸の交点Cを中心とする直径PQの円がモールの応力円となります。せん断応力τは、そのつり合いの関係から±のセットとなります。
図5で応力円と横軸の交点のうち、値の大きいほうの点Aが最大主応力σ1、小さいほうの点Bが最小主応力σ2を表します。
線分PCが横軸となす角度の2分の1=θが、最大主応力面への法線(最大主応力の方向)がx軸となす角度となり、測定された応力状態に対する主応力面と主応力の方向を求めることができます。
このようにモールの応力円は、荷重に対して物体内に発生する応力の状態と方向、あるいは測定された応力値から最大主応力、最大せん断応力の値と方向を知ることができる便利な手法です。
実務で使いこなせるように、確実に理解しておきましょう!
(日本アイアール株式会社 特許調査部 S・Y)