【機械設計マスターへの道】自重による応力とひずみ／自重を考慮した平等強さの計算

Pocket

自重と応力

当連載「機械設計マスターへの道」において、「荷重と応力、ひずみ」の関係について解説しました。

今回は機械自体の重さ（自重）による応力とひずみについて解説したいと思います。

自重による応力とひずみを計算する

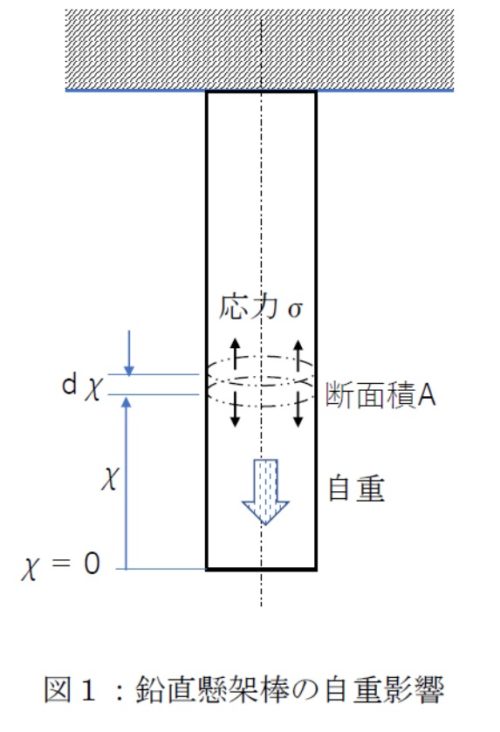
外部から荷重が加えられていなくても、下の図1のように長い棒の上端を固定して鉛直に懸架するなどの場合は、棒自体の重量（自重）によって生じる応力やひずみも無視できない大きさとなる場合もあるので、設計上注意が必要となります。

自重による応力とひずみ

自重による応力の計算

棒に使う材料の密度をρ[kg/m³]、棒の断面積をA[m²]　とすれば、棒の下端から距離χ[m]　にある断面には、該断面より下にある部分の質量ρAχに重力加速度g [m/s²]を乗じた値が引張荷重として作用しますから、該断面に生じる引張応力σは
　σ=ρAχg/A=ρχ g [m^-1・kg・s^-2]= ρχ g/10⁶[MPa] 　・・・(1)
となります。

鉄鋼材料の密度ρ=7.85×10³[kg/m³]、重力加速度g =9.8[m/s²]とすれば、例えば棒の下端からχ =5[m]の位置で自重による生じる応力は（1）式より、以下のようになります
　σ=7.85×10³ x 5 x 9.8 x10^-6= 0.38[MPa]

棒の材料が一般構造用圧延鋼材SS400であるとすれば、その引っ張り強さは400[MPa]であり、上記の自重による応力は特に問題ない値のように考えられます。

自重による「ひずみ」と変形の計算

次に自重によって生じる　ひずみと変形（伸び）についても考えてみましょう。

棒材のヤング率をE[MPa] とすれば、棒の下端から距離χ [m]　にある断面におけるひずみは、
σ/E=ρχ g/(Ex10⁶) となります。

棒の下端から距離χ [m]　にある微小部分dχ の伸び⊿λは、
　⊿λ=ρχ g/(Ex10⁶) dχ
であり、棒の全長をL[m]とすれば、棒全体の伸びλは次のようになります。
　

また、棒材のヤング率E=206×10³[MPa] とすれば　L=5[m]のとき棒全体の伸びは（2）式より
　λ=7.85×10³ x 9.8 x 5² /(2x 206 x10⁹)=4.67×10^-3[mm]
となり、自重により発生する伸びも特に問題ない数値のようです。

しかし、実際の機械構造においては様々な外部荷重が加わり、また単純引張だけでなく、曲げ、せん断など荷重条件も多様となります。
自重により発生する応力や伸び（ひずみ）の基本的な求め方を理解しておくことは重要です。
また外部荷重が加わったときに、長棒による懸架構造を、より合理的に設計するためにも役立ちます。

自重を考慮した、平等強さの計算

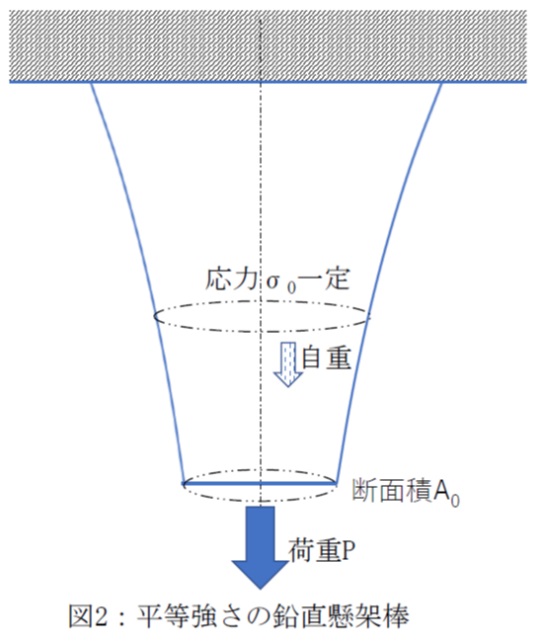
天井から鉛直に懸架された棒の下端（底面）に荷重Pが作用するとき、荷重Pと棒の自重によって発生する応力が、棒の全長にわたる各断面で一定値となる、平等強さ形状を求めてみましょう。

棒の下端を座標原点とし、下端の棒断面積をA₀とします。
下端における応力をσ₀とおけば
　σ₀ = P/ A₀　・・・(3)
となります。

下端から距離χの位置における棒の断面積をAとし、微小長さdχにおける力のつり合いを考えます。
dχ間の面積の増分をdAとするとき、この微小長さ領域の増分断面積に作用する自重による応力がσ₀に等しくなるように断面変化形状を設計できれば良いことになります。

したがって、まず、
　σ₀ = ρg A dχ/dA　・・・(4)
という(4)式の変数を分離すれば、
　dA/A =　(ρg / σ₀) dχ　・・・(5)
となり、この(5)式両辺を積分して
　lnA = 　(ρg / σ0) χ+C
　A = e^{(ρg / σ0) χ} ・e^C　・・・（6）
（e：自然対数の底）
となります。