【電気数学をシンプルに】電気回路の解析⑤ 3×3行列を用いた行列法［ホイートストンブリッジの例］

Tweet

Pocket

今回は、3×3行列を用いた行列法を使って連立方程式を解いていきます。

［※2×2行列を用いた方法は「電気回路の解析④ キルヒホッフの法則と行列法」をご覧ください。］
 

１．ホイートストンブリッジの平衡条件を求める

《問題》

図1の回路において、抵抗R_Gに流れる電流I_G=0となる条件を求めてみましょう。

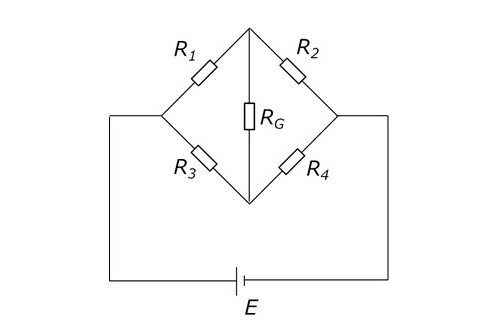
［図1　ホイートストンブリッジ］

求める方法は一通りとは限りません。
本問では、キルヒホッフの法則を用いて閉路方程式を立てて解いていく例を紹介します。
 

２．閉路電流法(閉路方程式)を3×3行列を用いた行列法で解く

《解説》

閉路電流法（閉路方程式）を用いた場合の解き方

手順は以下の通りです。

• ①：閉路を見つける。
• ②：閉路に流れる電流を未知数にする。電流の向きも決める。
• ③：キルヒホッフの電圧則を適用する。

この手順に従うと、
①ここでは、図2で示される黄色部分、緑色部分と水色部分の3つの閉路を見つけたとします。
②各閉路に流れる電流をそれぞれ未知数I₁、I₂、I₃とし電流の向きは図2における矢印の向きとします。

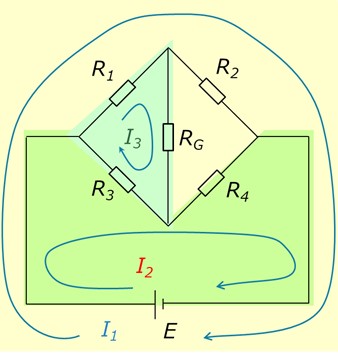
［図2　3つの閉路と電流の向き］

③キルヒホッフの電圧則を適用して方程式をたてます。

黄色部分の閉路について、
オームの法則より、V=RI
E＝(I₁+I₃)R₁ +R₂I₁

緑色部分の閉路について、
E＝(I₂–I₃)R₃ +R₄I₂

水色部分の閉路について、
(I₃+I₁)R₁ +I₃R_G+(I₃–I₂)R₃＝0　←キルヒホッフの電圧則

式を整理して、I1、I2、I3の連立一次方程式にして解きます。

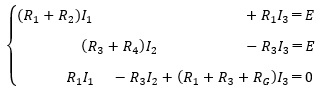
まず、連立一次方程式を行列で表現します。

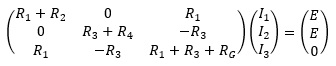
両辺に左から逆行列をかけます。

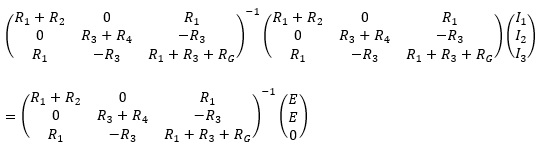
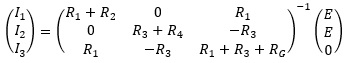
ここで、逆行列　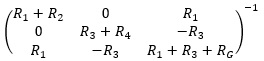　を計算します。

［※3×3行列の逆行列の求め方は「電気回路の解析③ 逆行列と行列式」をご参照下さい。］

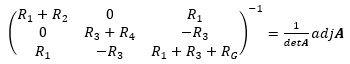
余因子行列adjAを求めます。

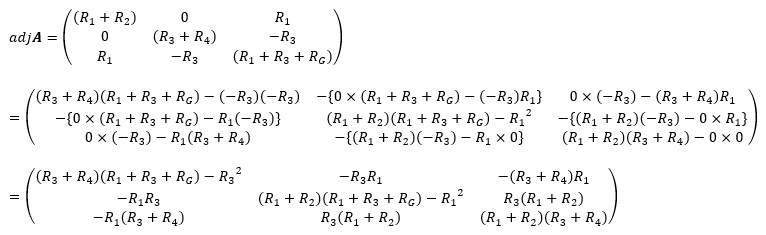
よって、

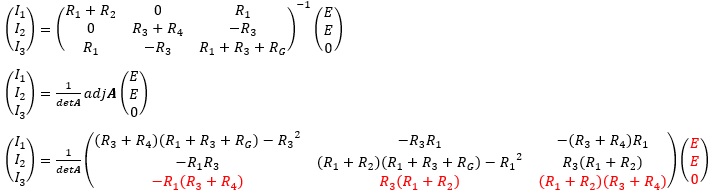
ここで、抵抗R_Gに流れる電流I_G=0となるためには、I₃=0になればよいので、式の赤字部分を取り出して、I₃のみ計算すると、

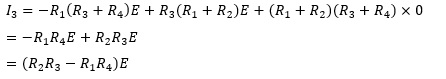
したがって、
I₃=0になるのは、R₂R₃-R₁R₄=0、すなわち、R₁R₄ = R₂R₃のときになります。
以上より、I_G=0となるための条件は、R₁R₄ = R₂R₃になります。

《参考》
本問を解くためには、行列式の値まで求める必要はありません。
行列式detAの値を求めます。

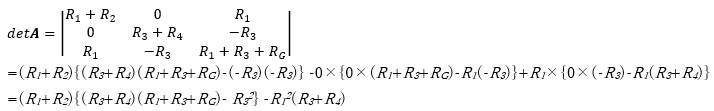
３．ホイートストンブリッジについて

図1の回路は、主に高精度の抵抗測定回路として使われています。
物理学者ホイートストン（Charles Wheatstone）が伝えたブリッジ回路ということで「ホイートストンブリッジ」と呼ばれます。「ブリッジ回路」とは、図1のように1本の導線から2つの並列回路に分かれた後また1本の導線で再結合する電気回路のことです。

また、問題で求めた電流I_G=0となる条件を「平衡条件」といいます。
平衡している（R₁R₄ = R₂R₃が成り立つ）ときは、抵抗R_Gがない状態と同じなので、図1の4つの抵抗R₁、R₂、R₃、R₄のうち3つの値がわかれば残りの1つの値を知ることができます。
つまり、ブリッジ回路をつくり、中間点の電流を0になるように調整することで、未知の抵抗の値が測定できるのです。
 

（日本アイアール株式会社　N・S)
 

Tweet

Pocket