【電気数学をシンプルに】電気回路の解析④ キルヒホッフの法則と行列法

Tweet

Pocket

今回のコラムでは、行列法を用いて実際に電気回路を解析する問題をご紹介します。

※連立一次方程式や行列法の前提知識については次の各コラムを参照下さい。

• 電気回路の解析① 行列の基本《連立一次方程式を行列法で解く》
• 電気回路の解析② 行列の演算方法をチェック

１．2つの電源を含む回路を解析する

《問題》

早速ですが、キルヒホッフの法則を用いて図1の回路を解いてみましょう。
（回路に流れる電流を求めてみましょう。）

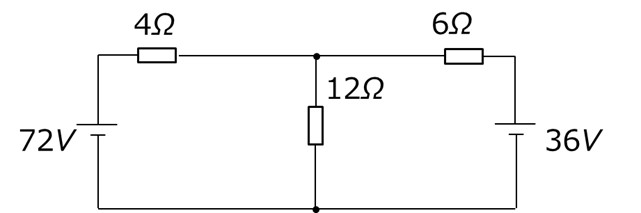
［図1　２つの電源を含む回路］

回路を解析するときは、未知数のとり方によって立てる方程式が変わってきます。

本問では、”キルヒホッフの法則を用いて”と問われていますので、解説1として閉路方程式、解説2として節点方程式を立てて解いていく一例を紹介します。
 

２．閉路電流法（閉路方程式）を2×2行列を用いた行列法で解く

《解説1》

閉路電流法（閉路方程式）を用いた場合の解き方

手順は、
① 閉路を見つける。
② 閉路に流れる電流を未知数にする。電流の向きも決める。
③ キルヒホッフの電圧則を適用する。
になります。

この手順に従うと、
①ここでは、図2で示される黄色部分と緑色部分の閉路を見つけたとします。
②黄色部分の閉路と緑色部分の閉路に流れる電流をそれぞれ未知数I₁、I₂とし、電流の向きは図2における矢印の向きとします。

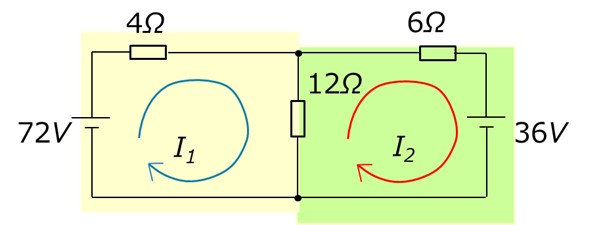
［図2　2つの閉路と電流の向き］

③キルヒホッフの電圧則を適用して方程式をたてます。

黄色部分の閉路について、
オームの法則より、V=RI
　72＝4I₁+12(I₁-I₂)　← キルヒホッフの電圧則
緑色部分の閉路について、
　36＝-6I₂+12(I₁-I₂)
式を整理して、I₁、I₂の連立一次方程式にして解きます。

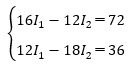
まず、連立一次方程式を行列で表現します。

両辺に左から逆行列をかけます。

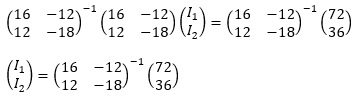
ここで、逆行列　を計算します。

行列式の値を求めます。

=16×(-18)-(-12)×12
=-288+144
=-144

よって、

したがって、

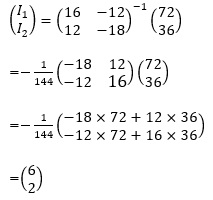
以上より、I₁=6、I₂=2の解が得られます。
解答例としては、図2における矢印の向きで電流I₁=6[A]、I₂=2[A]になります。

３．節点電圧法(節点方程式)を3×3行列を用いた行列法で解く

《解説2》

節点電圧法（節点方程式）を用いた場合の解き方

手順は、
① 接地点を任意に選ぶ。
② 電源に流れる電流を未知数にする。電流の向きも決める。
③ 接地点以外の節点にキルヒホッフの電流則を適用する。
になります。

この手順に従うと、
①ここでは、図3の中央下に示される接地点を選んだとします。
②左側の電源72[V]と右側の電源36[V]に流れる電流をそれぞれ未知数I_a、I_cとし電流の向きは図3における矢印の向きとします。

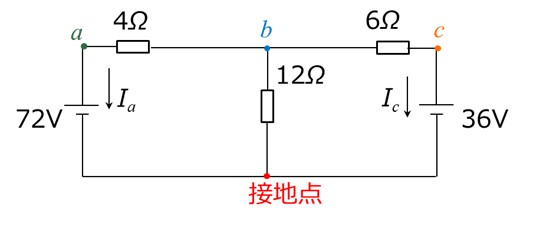
［図3　節点と電流の向き］

③図3に示した接地点以外の節点a、b、cにキルヒホッフの電流則を適用して方程式をたてます。

オームの法則より、V=RI

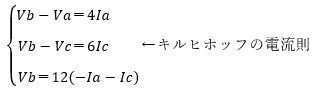
V_a＝72、V_c＝36であるから、

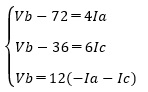
式を整理して、I₁、I₂の連立一次方程式にして解きます。

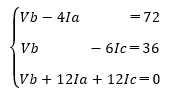
まず、連立一次方程式を行列で表現します。

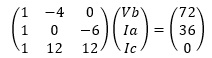
両辺に左から逆行列をかけます。

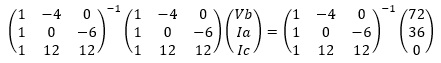
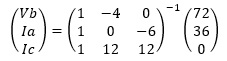
ここで、逆行列　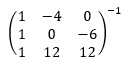　を計算します。

［※3×3行列の逆行列の求め方はこちらのコラムをご参照下さい。］
 

行列式の値を求めます。

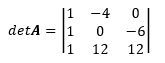
=1×0×12+(-4)×(-6)×1+0×1×12-{0×0×1+(-4)×1×12+1×(-6)×12}
=0+24+0-(0-48-72)
=144
よって、

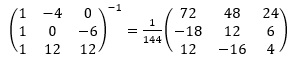
したがって、

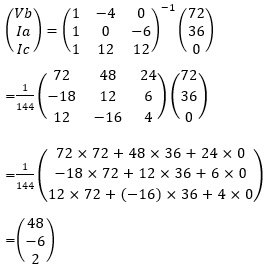
以上より、I_a=-6、I_c=2の解が得られます。
解答例としては、図3における矢印の向きで電流I_a=-6 [A]、I_c=2 [A]になります。

ということで今回は、実際に電気回路を解析する場面を想定し、行列法で電流を求める方法について解説しました。この問題を解くことにより、電気数学を学ぶ理由と必要性も理解いただけることと思います。

 
次回の連載コラムでは、ホイートストンブリッジを例とした問題について解説いたします。

（日本アイアール株式会社　N・S)
 

Tweet

Pocket