【電気数学をシンプルに】オイラーの公式と交流電圧
交流回路を解析して計算していくためには複素数を用いると便利です。
本コラムでは、虚数により三角関数と指数関数を結びつける「オイラーの公式」について解説します。
［※虚数については、当連載の「複素数とベクトル」の回をご参照ください。］
１．オイラーの公式とは
「オイラーの公式」は、一般的には、以下の式で表されます。
eix = cos x + i sin x （iは虚数）
左辺が指数関数で、右辺が三角関数で虚数により結びついた式です。
指数関数eixのeは「ネイピア数」と呼ばれる定数です。（e=2.718…）
さて、虚数と同様に、電気分野におけるオイラーの公式は、虚数iをj、xをθまたはωt(θ=ωt)と表記します。
ejθ = cosθ + j sinθは
オイラーの公式により三角関数を指数関数に置き換えることで、三角関数の大変な計算をしなくて済みます。
このような計算の工夫は、特に微分方程式やフーリエ級数などを扱うときに重宝します。
また、オイラーの公式において、
θ=πのとき、
ejπ = cosπ + j sin π は
= -1 + 0
= -1
よって、ejπ + 1 = 0 となります。
この式は、「オイラーの等式」として、世界一美しい数式と言われています。
２．交流電圧の式を三角関数で表現する
交流波形は、サインカーブになり、y = sin ωtで表すことができます。
［※詳細は、当連載の「角速度と角周波数を求める」の回をご参照ください。］
図1に示すように、波形のピークがVmである交流電圧は、三角関数を用いて次式で表されます。
v(t) = Vm sin ωt
ここで、Vmは「最大値」、v(t)はある瞬間tでの値なので「瞬時値」といいます。
なお、一般に交流の値を表すのは実効値になります。
「実効値」とは、直流がする仕事と同じ仕事をする交流の値をいいます。
例えば、一般家庭での商用電源は交流100[V]ですが、この100[V]というのは実効値です。理論上は最大値が141[V]の正弦波交流になります。
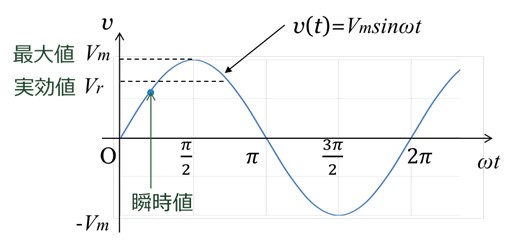
［図1 交流電圧 v(t) = Vm sin ωt ］
３．交流電圧の式を指数関数で表現する
それでは、三角関数で表された交流電圧の式をオイラーの公式にあてはめて、指数関数で表してみましょう。
オイラーの公式 ejθ = cosθ + j sinθ において、
θ = ωt であるから、
ejωt = cos ωt + j sin ωt
ここで、虚部をとります。（ejωt の虚部のみをとりだすときに、Im[ejωt]と表記します。）
Im［ejωt］=sin ωt
ejωt = sin ωt
となります。
交流電圧の式は、
v(t) = Vm sin ωt であるから、
v(t) = Vm sin ωt
= Vm ejωt
となり、指数関数で表すことができました。
図2に示すように、交流電圧の値は虚軸の値であるから、虚部のみをとって計算することができます。
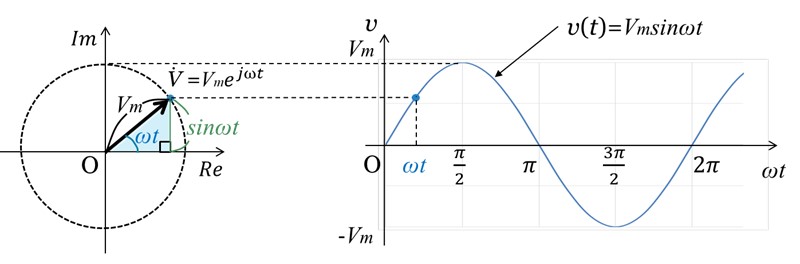
［図2 交流電圧を指数関数で表した図と三角関数で表した図］
以上のように、交流電圧の式は三角関数でも指数関数でも表すことができます。
場面によって使い分けることができますので、どちらの表記にも慣れておくことが必要です。
（日本アイアール株式会社 N・S)
