【電気数学をシンプルに】RLC直列回路とベクトル[ベクトル/三角関数/複素数の関係②]

交流は電流と電圧の向きと大きさが周期的に変化するため、ベクトルで表現することもできます。
今回は、電気回路に使われる代表的な素子である抵抗、コイル、コンデンサについて、実際にはどのようにベクトルを使っていくのかを解説します。
1.抵抗とベクトル
抵抗は、直流でも交流でも電流を妨げるはたらきをします。
図1には、左から抵抗の回路記号、ベクトル図、波形を示しています。
抵抗に交流電流が流れても、電圧vと電流iの位相が等しくなります(同相)。
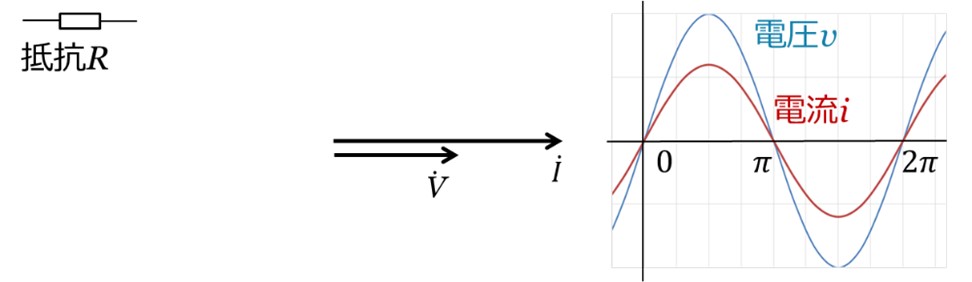
[図1 抵抗のベクトルと波形]
2.コイルとベクトル
コイルは、直流では短絡ですが、交流電流を妨げようとします。
この交流の流れにくさを「誘導リアクタンスXL」と呼びます。
また、コイルには自己インダクタンスがあります。
そのため、交流電流が流れると誘導起電力(逆起電力)が生じ続けます。
したがって、逆向きの電流を発生させる分電流が遅れます。
図2には、コイルの回路記号と電流iを基準にしたベクトル図、波形を示しています。
ここで、コイルは物理量がインダクタンスなので、回路中ではインダクタンスLと表記しています。
電流iは、電圧vに対して遅れ位相となります。
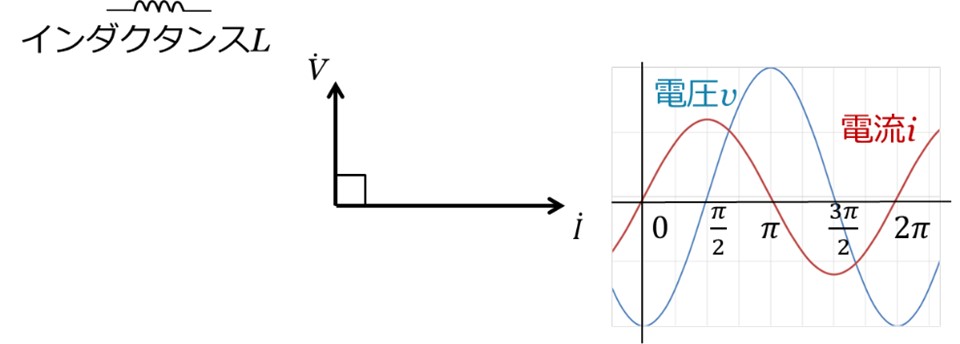
[図2 インダクタンスのベクトルと波形]
3.コンデンサとベクトル
コンデンサは直流では開放ですが、交流では、抵抗やコイルと同様に電流を妨げようとします。
この交流の流れにくさを「容量リアクタンスXC」と呼びます。
また、コンデンサには静電容量があります。
そのため、交流電流が流れると充電と放電を繰り返します。
したがって、充電される分電圧が遅れます。
図3には、コンデンサの回路記号と電流iを基準にしたベクトル図、波形を示しています。
ここで、コンデンサは物理量が静電容量なので、回路中では静電容量Cと表記しています。
コイルと異なり、電流iは、電圧vに対して進み位相となります。
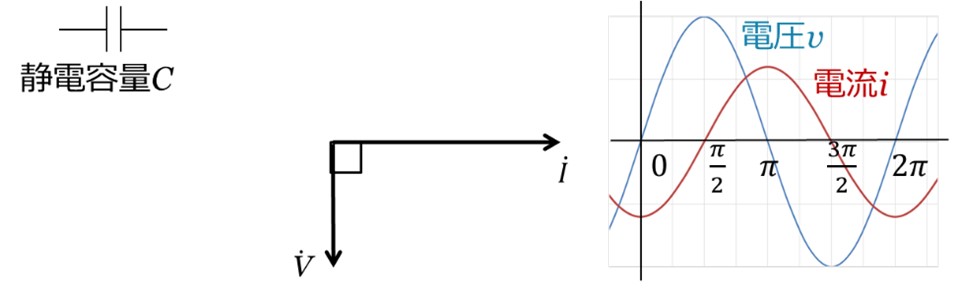
[図3 静電容量のベクトルと波形]
4.RLC直列回路におけるベクトルの使い方
以上の内容をふまえて、図4に示した抵抗、コイル、コンデンサを直列接続して交流電源につないだRLC直列回路におけるベクトルの使い方を解説します。
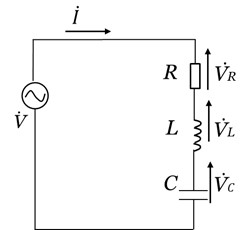
[図4 RLC直列回路]
(1)各素子における電圧と電流のベクトルの関係
交流回路でコイルやコンデンサが使われているときには、どちらも電流を妨げようとすることの他に、位相を考慮しなければなりません。
図5は、各素子における電圧と電流の関係を表したベクトル図です。すべて電流![]() を基準にしています。
を基準にしています。
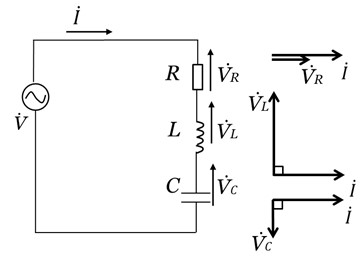
[図5 RLC直列回路と各素子における電圧と電流のベクトル図]
ここで、直列回路の合成インピーダンスZは、抵抗RとリアクタンスXの和になるので、
Z=R+XL+XC
となります。
では、各素子のベクトルを合成します。
![]() =
=![]() +
+![]() +
+![]()
(2)合成ベクトルの求め方
実際には、回路全体の電圧![]() は
は![]() と
と![]() の関係で決まります。つまり、誘導リアクタンスXLと容量リアクタンスXCとの大小で決まり、回路の特性が確定します。
の関係で決まります。つまり、誘導リアクタンスXLと容量リアクタンスXCとの大小で決まり、回路の特性が確定します。
そのため、図6に示したように、まず、![]() +
+![]() から求めていきます。
から求めていきます。
![]() =
=![]() +(
+(![]() +
+![]() )
)
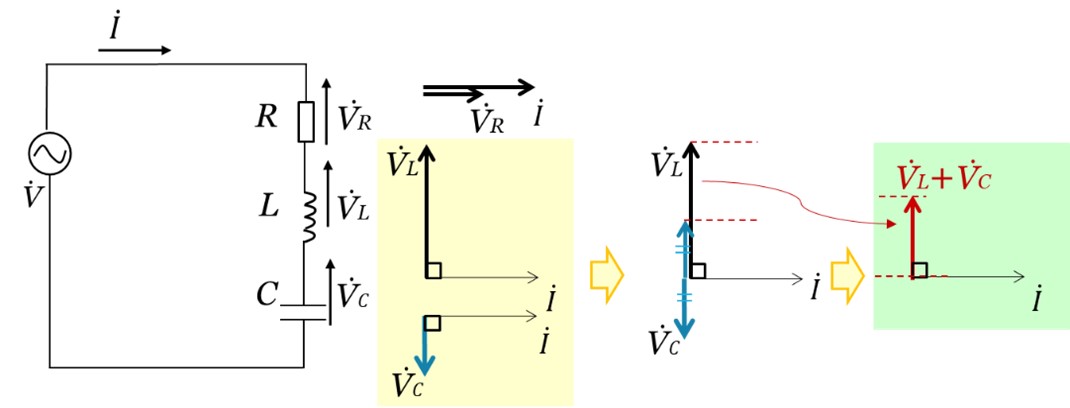
[図6 RLC直列回路における(![]() +
+![]() )を合成したベクトル図]
)を合成したベクトル図]
![]() と
と![]() は、向きが逆であるから、その合成ベクトル
は、向きが逆であるから、その合成ベクトル![]() +
+![]() は、大きさにより
は、大きさにより![]() または
または![]() のどちらかの向きになります。
のどちらかの向きになります。
図6では、![]() の大きさが
の大きさが![]() の大きさよりも大きいので、合成ベクトル
の大きさよりも大きいので、合成ベクトル![]() +
+![]() は
は![]() の向きになります。
の向きになります。
次に![]() +(
+(![]() +
+![]() )を求めていきます。
)を求めていきます。
図7に示したように、先ほど求めた、![]() +
+![]() (赤いベクトル)と
(赤いベクトル)と![]() の合成ベクトルを考えることで、回路全体の電圧V ̇を求めることができます。
の合成ベクトルを考えることで、回路全体の電圧V ̇を求めることができます。
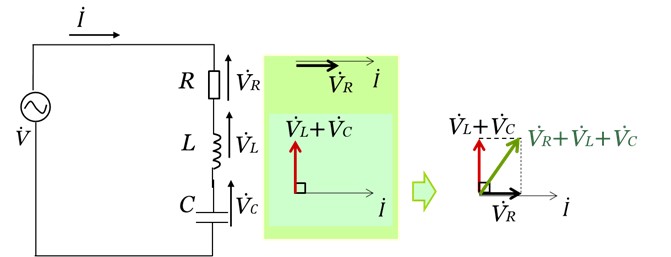
[図7 RLC直列回路における![]() +(
+(![]() +
+![]() )を合成したベクトル図]
)を合成したベクトル図]
以上がRLC直列回路における各素子のベクトルの関係になります。
このあと電圧![]() の大きさを求めていくためには、複素ベクトルを用いると便利です。
の大きさを求めていくためには、複素ベクトルを用いると便利です。
[※複素ベクトルについては別のコラムで解説予定です。]
(日本アイアール株式会社 N・S)














](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)































