2021.06.14 2024.06.03

【電気数学をシンプルに】角速度と角周波数を求める

角速度と周波数の解説

本連載の最初のコラムにおいて、交流波形をベクトルとして考えることができることを紹介しました。

交流波形を考えるには円運動の知識も必要になります。
なぜなら、原点Oを始点とする単位ベクトルの終点は単位円上を円運動するからです。
（※詳細は、別コラム「ベクトルと位相・位相角」のページをご覧ください）

今回のコラムでは、円運動を考えた場合の角速度について解説します。

１．位相角θと角速度ω

図1に示すように、原点Oを始点とする単位ベクトルを考えたとき、単位ベクトルの終点は単位円を円運動します。
そこで、ベクトルが向く角度の時間変化量をω[rad/s]とすると、ωは角速度にあたります。
つまり、角速度ωとは、円運動している点が1秒間に進む角度を表しています。
したがって、位相角θは角速度ωと時間tの積で求めることができます。

　θ=ωt

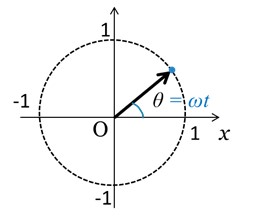
［図1 位相角と角速度の関係］

２．周期Tと周波数f

位相角θは、角速度ωと時間tの積になることから、図2のように、交流波形は、横軸をωt、縦軸をyとするとy=sinωtで表すことができます。

ここで、y=sinωtは、山と谷を繰り返していく波形になります。

波形において、繰り返しの最小単位となる山と谷の1セットを1サイクル（周波）といい、1サイクルに要する時間をT［s］といいます。
周期Tは、図2左の円周を一周する時間に当たります。また1秒間のサイクル回数を周波数f［Hz］といいます。

つまり、周期Tと周波数fには次式の関係が成り立ちます。

　f=1/T

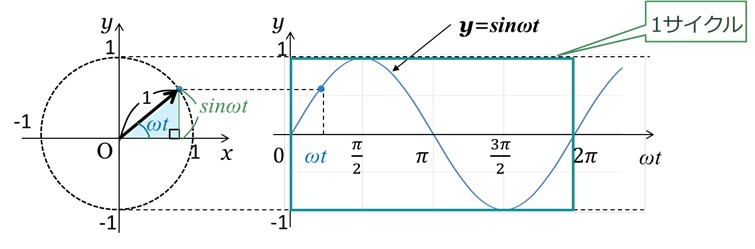
［図2　y=sinωtの1サイクル（周波）］

３．角周波数

図2左の単位円を一周する場合を考えてみましょう。

位相角θは、角速度ωと時間tの積になることから、
　θ=ωt
ここで、単位円の円周角は円周と等しく2πなので、
　ωt=2π
このとき、円周を一周する時間は周期T であるから、t=Tになります。したがって、
　ωT =2π
周期は周波数の逆数（f=1/T）なので、
　ω=2πf
になります。

つまり、角速度ωは、周波数fをを2π倍したものになります。
そのため、角速度ωは2π倍の周波数なので、「角周波数」とも呼ばれています。
交流に限らず、周期的な現象を扱う場合には、周波数よりも角周波数を用いるのが一般的です。
その理由は、もちろん計算が楽になるからです。