【電気数学をシンプルに】複素数とベクトル（位相の表し方）
交流回路を解析して計算していくためには複素数を用いると便利です。
本コラムでは、複素数と複素平面上におけるベクトルについて解説します。
１．複素数と複素平面上におけるベクトルの基本
複素数Zは、2つの実数a、bと虚数jを用いて表すことのできる数です。
Z=a+jb
aを実部（Real）、bを虚部（Imaginary）といいます。
図1左に示したように、複素数Zは、横軸を実部Re、縦軸を虚部Imとする複素平面上において、点（a, b）と考えることができます。
また、図1右のように、複素数Zは、原点Oと点（a, b）を結ぶベクトルで表すこともできます。
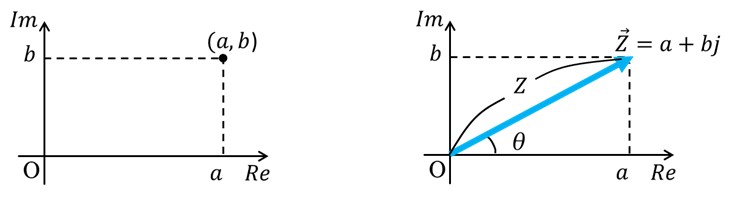
［図1複素平面上の点（a, b）とベクトルZ］
２．虚数とベクトルの対応
虚数（Imaginary number）は、2乗したらマイナス1になる数として定義されています。
つまり、
です。
ここで、実数1にjをかけていくと
1×j = j
j ×j =j2= -1
j2×j =j3= -j
j3×j =j4= 1
j4×j =j5= j
……というように1, j, -1, -j, 1,……の値を繰り返しとります。
この値を複素平面上にベクトルとして表したのが図2になります。
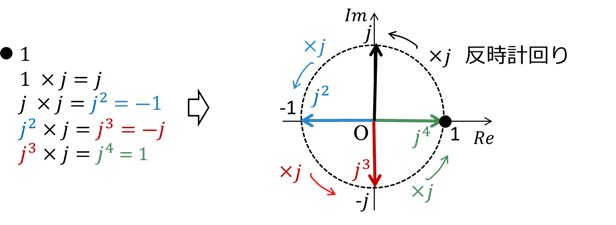
［図2 虚数jの乗算と複素平面におけるベクトルとの対応］
図2右に示されたベクトルの動きから、虚数jの乗算は、ベクトルが反時計回りに90°回転することに対応していることがわかります。
同様に、虚数-jの乗算は、ベクトルが時計回りに90°回転することに対応します。図3に図示します。
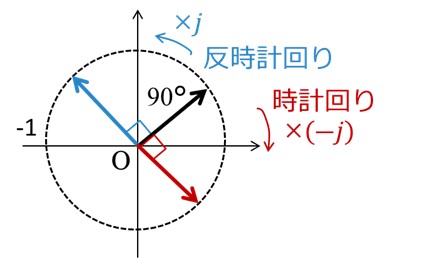
［図3 虚数jの乗算および虚数-jの乗算と複素平面におけるベクトルとの対応］
３．位相と複素数の関係（虚数を用いた位相の表し方）
反時計回りに90°回転というと、位相と位相角の対応を思い出された方もいらっしゃると思います。
位相角が反時計回りに90°回転することを、”90°位相が進む” と表現しました。
（※詳細については「ベクトルと位相・位相角」の回をご覧ください。）
虚数jをかけていくとベクトルが反時計回りに90°回転することがわかりましたので、虚数を用いて位相を表してみます。
例えば、コイルの場合、交流電流iは、電圧vに対して遅れ位相となることを取り上げてみます。
まず、オームの法則より、直流においては、電圧は電流と抵抗の積になります。
交流においても電圧の大きさは電流の大きさとインピーダンスの大きさの積になります。
V=IZ
交流では位相を考慮する必要がありますので、電圧と電流は大きさと向きをもつベクトルで考えます。
電圧vは電流iよりも位相がπ/2進みます。ベクトルで描くと図4左のようになります。
このことは、複素平面上では、電圧
は電流
に虚数jをかけることに対応しています（図4右）。
=jZ
要するに、この式を見ただけで、電圧は電流に虚数jをかけているから、位相がπ/2進んでいるということがわかります。
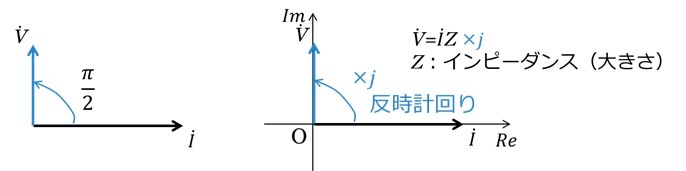
［図4 位相がπ/2進むことと複素数の関係］
同様に、コンデンサの場合、電圧vは電流iよりも位相がπ/2遅れます。
複素平面上では、電圧は電流に虚数-jをかけることに対応しています（図5）。
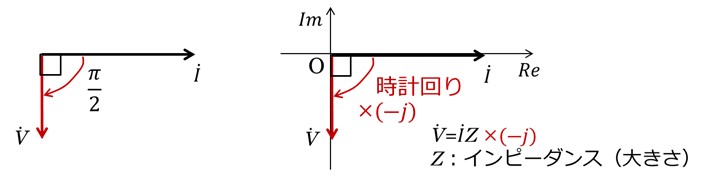
［図5 位相がπ/2遅れることと複素数の関係］
以上より、複素数で位相を表していることと、複素数の式を計算することが位相の計算もしていることになっているのがわかります。
（日本アイアール株式会社 N・S)
