【QC検定3級対策】工程能力指数の判断基準とCp・Cpkの計算問題

QC検定は、JSA日本規格協会グループが主催する品質管理の知識を問う筆記試験です。
内容は品質管理とは何か?から始まり、改善活動の基礎知識、統計的なプロセス管理など多岐にわたります。
受験者数は年々増加しており、毎年の受験者数が10万人を超える製造業ではメジャーな試験です。
[※関連記事:【技術系資格ナビ】QC検定(1〜4級の難易度/合格率/勉強方法/メリット)はこちら]
この連載では、各級の頻出範囲について例題を交えて解説を行います。この連載を通じて、QC検定の受験準備をしてみましょう。
3級の試験範囲は日本規格協会のHP(品質管理検定レベル表)をご確認ください。
【3級解説:第6回】工程能力指数
(1)工程能力指数とは
「工程能力」とは規格内で生産できる能力、「工程能力指数」とはこの能力の程度を表す数値です。
一般的に工程能力指数は”Cp“(Process Capability Index)と表されます。
また規格が両側規格の場合、Cpだけではなく、平均値が規格の中央にあるかどうかを示す“Cpk“(Process Capability Index based on Katayori)を併用します。
工程能力指数の計算方法は下記の公式を用います。
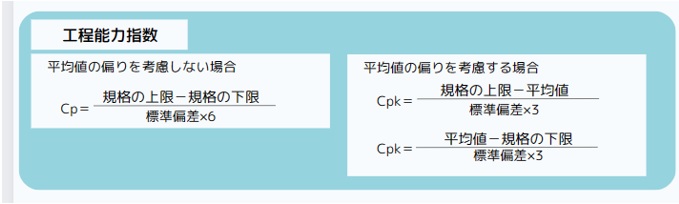
※関連コラム: 工程能力の詳しい解説は 【生産技術のツボ】工程能力の計算方法と評価方法がこれでわかる!両側規格と片側規格の計算事例 のページをご参照ください。
(2)工程能力指数の判断基準
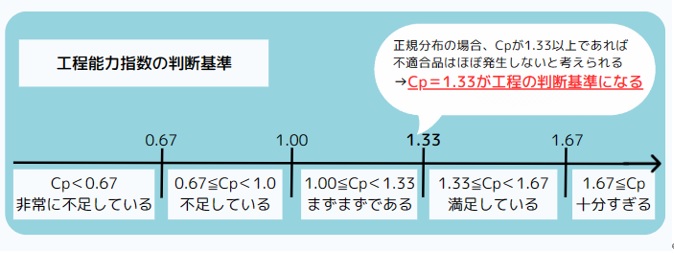
工程能力指数の判断基準については、QC検定3級では Cp=1.33 以上が工程能力が十分であるかどうかの判断基準になるということを覚えておきましょう。
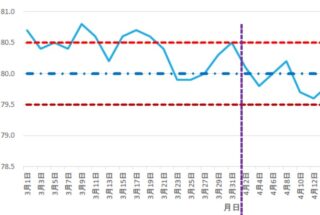
これは、平均値μ、標準偏差σの正規分布の場合に
- μ±σの範囲に入る確率は約68%
- μ±2σの範囲に入る確率は約95%
- μ±3σの範囲に入る確率は約99.7%
であることが知られているためです。
工程能力指数Cpは(規格上限-規格下限)÷(標準偏差σ × 6)なので、
規格の幅が6σの場合Cp=1.00、規格の幅が8σの場合Cp=1.33となります。
このことは工程能力Cpが1.33であれば規格を外れた不適合品はほとんど発生しないことを意味しています。
このためCp1.33以上が工程能力が十分である判断基準になります。
それでは例題にチャレンジしてみましょう。
《例題1》
工程能力指数に関する次の文章について正しいものには〇を、正しくないものには×を記せ。
ある工程で製造される部品の長さが平均10.7mm、標準偏差0.12mmの正規分布に従う。この製品の長さの規格は10.0±1.00㎜である。
① この工程の工程能力指数Cpは2.78である。
② この工程のかたよりを考慮した工程能力指数Cpkは4.72である。
③ この工程の工程能力指数Cpの評価は「十分満足している」と判断できる。
④ 一方、この工程の工程能力指数Cpkの評価は「十分満足している」と判断できる。
⑤ 標準偏差0.12mmのままできるだけ小さく改善することで平均をCpk=1.33とするためには、平均を10.7mmから10.5mm に改善する必要がある。
⑥ 平均値はそのままでCpk=1.33とするためには標準偏差を0.10mmに改善する必要がある。
《例題1》[解答と解説]
《例題2》
次の工程能力指数に関する文章について( )内に入る言葉を下の選択肢から選べ。
上限規格が85、下限規格が72、平均77、標準偏差2のとき、工程能力指数Cpは(①)、偏りを考慮したCpkは(②)である。
このとき、Cpkは(③)より大きく(④)より小さいので「不足している」と言える。
このため、(⑤)を早急に調査して工程を改善する必要がある。
選択肢
[ア.0.67 イ.1.0 ウ.1.33 エ.1.67 オ.原因 カ.結果 キ.0.50 ク.0.83 ケ.1.08 コ.3.25]
《例題2》[解答と解説]
まとめ
今回は工程能力指数について解説しました。
工程能力指数は管理図とともに実際の製造工程でも非常に重要な概念ですので、ぜひマスターしましょう。
次回は手法分野の最終章「相関分析」について解説します。
(アイアール技術者教育研究所 A・K)