き裂の進展と応力拡大係数について丁寧に解説｜疲労き裂のメカニズムと設計上の注意点がわかる！

Tweet

Pocket

１．き裂（亀裂）の発生

機械部材には、キー溝、段付き、などの応力集中部があります。また溶接構造では、溶接ビードと母材との境界部（止端部）などが応力集中部となります。

機械を使用して部材が負荷を受けることにより、これらの応力集中部の金属組織にずれが起きて、「き裂」（亀裂、crack）が生じることがあります。
負荷を受けることにより発生する、つまり使用期間中に発生するき裂の他にも、加工や溶接により発生した残留応力などの要因により製造時に発生する、非破壊検査で検出されない微細なき裂もあります。

機械の使用期間中に、き裂が進展すると、やがて破壊に至ります。
特に、繰り返し応力を受けるような使われ方をする機械の場合、繰り返し応力の大きさとその変動幅により、き裂が進展して疲労破壊に至るかどうか検討することが重要となります。

２．応力拡大係数とは

「応力拡大係数」（stress intensity factor）Kとは、き裂先端における応力やひずみの厳しさ度合いを示す量であり、次の式で表されます。

　　　　　・・・（1）
　F：き裂の形状や、母材との寸法比によって定まる無次元係数

Fは、き裂長さが小さい範囲では一定値とみなすことができます。
き裂長さが大きくなると母材寸法に対するき裂長さの比の関数となります。

• σ：き裂が無いとした場合の応力（公称応力）
• ａ：き裂の長さ

応力拡大係数の単位は、MPa・m^0.5で、切欠きを有する金属部材の破壊に対する抵抗力を示す指標として使われる破壊靭性値も同じ単位となります。

式（1）の係数Fの具体的な値を、図1のような3通りのき裂位置の場合における例について示します。

１）半無限板の片側に亀裂のある場合

　　　　　・・・（2）

厳密には、（1）式の係数Fは、き裂長さと板の幅の比の関数となりますが、aに比べて板幅が十分大きい場合は（2）式を適用することができます。

２）半無限板の中央に亀裂のある場合

　　　・・・（3）

ここでは図1（2）に示す、き裂全長2aに対して、aを用います。

３）有限板の中央に亀裂のある場合

　　　　・・・（4）

厳密には、（1）式の係数Fは、に、さらに、き裂全長2aと板の幅Wの比の関数をかけた形となりますが、近似式として応力拡大係数は（4）式を適用して求めることができます。

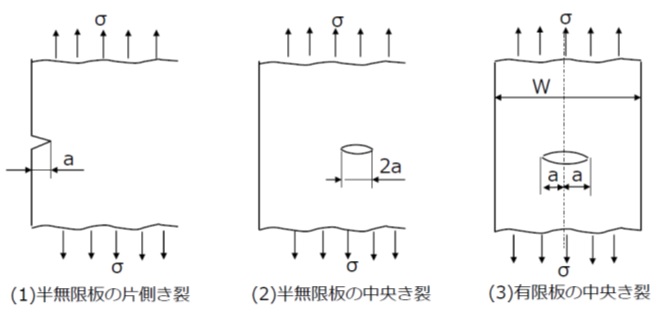
【図1　板に生じるき裂形状の例】

３．疲労き裂の進展

外力が変動して繰り返し機械部材に作用するとき、繰り返し応力による「疲労き裂」（疲労亀裂）の進展が問題となります。

外力の変動幅に対応する応力拡大係数の変動幅のことを応力拡大係数範囲⊿Kといいます。

変動する外力により発生する最大応力をσ_max、最小応力をσ_min、応力拡大係数最大値をK_max、最小値をK_minとするとき、

　　　　・・・（5）

応力の繰り返し1回あたりの疲労き裂長さの進展のことを、「き裂進展速度」（亀裂進展速度）といい、da/dnで表します。
⊿Kの、き裂進展速度da/dnの関係は、一般的に図2のような形になり、３つの段階に分けて考えることができます。

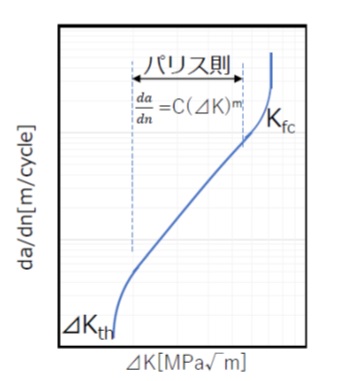
【図2　⊿Kと疲労進展速度の関係（両対数）】

１）き裂進展が不連続の領域（⊿Kが小さい領域）

疲労き裂進展の機構は不連続的で、材料の微視的組織や環境の影響を強く受けます。
⊿Kが小さい領域では⊿Kが減少すると、き裂進展速度が急激に減少していき、ある⊿Kにおいて、き裂進展速度が0となり、き裂進展が停止します。
このときの⊿Kを「下限界の応力拡大係数範囲」（threshold stress intensity factor range）といい、⊿K_thで表します。この値は、部材に存在または発生した微細な欠陥やき裂から、き裂が進展するか否か（有害性の有無）を判断するときの重要な指標となります。⊿K_th以下であれば、き裂は成長せず疲労破壊しないということがいえます。そういった意味で、S-N線図における疲労限度応力と対比して考察しながら強度設計に利用することができます。

鉄鋼材料における⊿K_thの値は目安として6～10[MPa ]　程度といわれています。

２）安定的な連続進展の領域（⊿K中間領域）

⊿Kの中間領域においては、安定した疲労き裂の進展が見られるようになります。
⊿Kとda/dnの関係は両対数で表したとき直線性を示します。

また、この領域における疲労き裂進展は連続的で、疲労破面には「ストライエーション」と呼ばれる応力の繰り返しごとにき裂が進展した痕跡である縞状の模様が形成されます。
この領域では微視組織や応力比、環境などの影響は比較的小さくなります。

この領域における安定した疲労き裂進展について、Parisらは式（6）で表されるべき乗関係が成立することを見出しました。

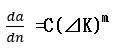　　　　・・・（6）

この関係のことを「パリス則」（Paris’s rule）といいます。
様々な材料や条件を規定した疲労き裂進展試験法が制定されていて、試験から得られたべき乗数mと定数Cに関するデータ集が発行されています。
m値としては2～7程度の値となることが知られています。

３）不安定破壊に至る領域（⊿Kが大の領域）

き裂進展速度と⊿Kの関係が両対数で表したとき線形となる中間領域より⊿Kが大きくなると、き裂が急激に進展する不安定破壊の領域となります。き裂の進展に伴い荷重を負担する部材の断面積が減少するため、き裂の進展速度が加速度的に増加して、応力拡大係数最大値K_maxが材料の疲労破壊靭性値K_fcを超えたときに破壊します。

すなわち不安定破壊の条件は次の式で表されます。

　K_max≧K_fc

なお、破壊靭性値には静的破壊靭性値と疲労破壊靭性値とがあって、疲労破壊靭性値は静的破壊靭性値よりも若干小さい値となります。また温度の影響を大きく受ける値であるので注意が必要となります。

４．疲労き裂進展に影響する因子

１）応力比の影響

応力比が負となる、すなわち引張と圧縮を繰り返し受けるような負荷状況の場合には、圧縮時にき裂が閉口することによって疲労き裂進展に対する抵抗が大きく増大します。
このため、同一の応力拡大係数範囲であっても、正の応力比（引張‐引張）の場合に比べて、き裂進展速度は小さくなります。

２）温度の影響

一般的に温度が上昇すると、疲労き裂進展速度は速くなります。

３）切欠きの影響

キー溝などの切欠きや孔から発生したき裂は、切欠き底部における応力集中の影響を受け、き裂進展速度は速くなります。特に応力拡大係数範囲が小さい領域で影響が大きくなるので注意が必要です。

４）材料の影響

き裂進展速度は、材料によって違いが生じます。特に高張力鋼の場合は、下限界の応力拡大係数範囲⊿K_thが低くなり、微細欠陥や加工傷などに対して敏感となるので注意が必要です。
また材料によっては熱処理温度や板厚の違いによる影響を受けるものがあります。

５．疲労き裂進展寿命推定

パリス則が適用できる中間領域の⊿Kでは、定数m、Cがわかればパリス則の式（6）をき裂長さで積分することにより、疲労き裂進展寿命を推定することができます。
き裂長さが小さい範囲では式（2）、（3）、（4）の例のように、式（1）における係数Fを一定値とみなすことができるので、き裂寸法が初期値a₁からある長さa₂まで成長するまでの繰り返し数（寿命）Nは、式（1）、（6）より

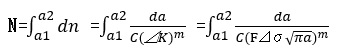　　　　・・・（7）

（7）式の解は、mが2ではないとき

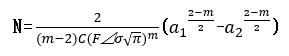
m=2のときは

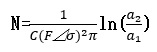
き裂寸法がある程度大きくなると、Fはき裂と母材の寸法比の関数となるので、上記の解は適用できなくなります。数値積分法などの手法を用いて、き裂進展寿命を推定する必要がありますが、微小な範囲におけるき裂の進展寿命を簡便に推測するためには、上記の解法を適用することができます。
 

以上、今回は機械を設計する上で最低限知っておくべき「疲労き裂の進展メカニズム」について概要を解説しました。

（日本アイアール株式会社　特許調査部　S・Y）
 

Tweet

Pocket