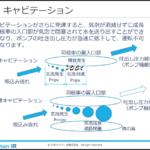
ベルヌーイの定理を応用した流量・流速の測定 [オリフィス流量計/ベンチュリ管/ピトー管]

以前の本連載コラムでは、流体力学の基礎知識として「連続の式とベルヌーイの定理」を解説しました。
今回は、ベルヌーイの定理を応用した流量と流速の測定について紹介します。
1.オリフィス流量計
オリフィス流量計の原理
管路の途中にフランジで挟むなどして設置される、内径よりも小さい穴を空けた薄板形状の部品を「オリフィス」といいます。流路面積が絞られることで抵抗となり、オリフィス前後に生じる圧力損失を利用して、流量を測定することができます。
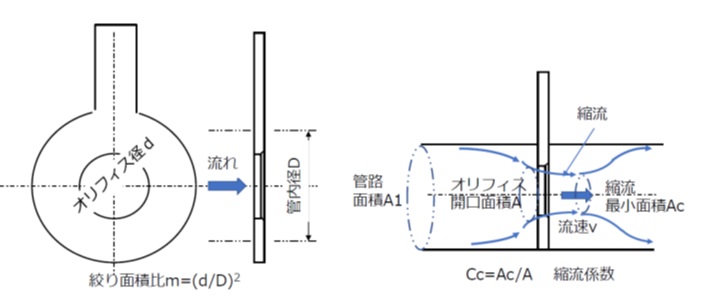
【図1 管路内のオリフィス(縮流と縮流係数)】
管路内の流れはオリフィスで絞られて、流体の慣性のためにオリフィスの下流で断面積が最小となります。このような流れを「縮流」といいます。
また、流れの最小面積をAc,オリフィスの開口面積をAとするとき、Cc=Ac/Aを「縮流係数」といいます。
オリフィス流量計の計算
オリフィス板の上流部と下流の最小流れ面積部にベルヌーイの定理を適用すると、オリフィスが水平な流れに置かれ、位置エネルギーの変化がないとすれば
1/2ρV12+p1=1/2ρV22+p2 ・・・(1)
[※ ρ:流体の密度、添字1はオリフィス上流、2は下流の縮流部]
オリフィス前後の流れには、連続の式を適用することができるので、上流の面積をA1 下流の最小流れ面積をAc、流量Qとすれば、
Q=A1V1=AcV2=CcAV2 ・・・(2)
オリフィス下流の縮流部における実際の流速vは、流れのはく離による損失が生じるため、V2よりも若干小さくなります。
v=CvV2
ここでCvを「速度係数」といいます
(1),(2)式を、速度係数を用いて整理すると
流量Q=αA√(2(p1-p2)/ρ) ・・・(3)
と書くことができます。
ここでαは「流量係数」といい、次式のようになります。
α=CcCv/√ (1-Cc2m2) ・・・(4)
(ただし m=A/A1・・・オリフィス絞り面積比)
流量係数を測定する際の注意点
流量係数は、多くの実験に基づく図表や式が用意されており、それらの資料から読み取ります。
管路内の流れの乱れの影響を避けるため、オリフィスは直管部に取り付け、上流は管内径の5~80倍程度、下流は4~8倍程度をとることが必要とされます。また、オリフィス内径部が摩耗すると測定誤差が生じてしまうため、流体中への固形物の混入を避ける必要があります。
上記のような注意点を守れば比較的高い測定精度が得られるので、オリフィス流量計は、ポンプの性能試験に多く使用されます。
ポンプ性能試験は、吐出しから吸込みへの循環経路配管を用いてポンプを運転しますので、オリフィスによる減圧は吐出し圧から吸込み圧へ戻す点においてむしろ好都合となるのも利点です。低揚程ポンプの場合は、せき(Weir)を用いて流量測定を行います。
オリフィス前後の圧力取り出し口を「オリフィスタップ」といい、JIS Z8762「絞り機構による流量測定」では、フランジタップ、コーナータップ、D・D/2タップの3種類が規定されています。
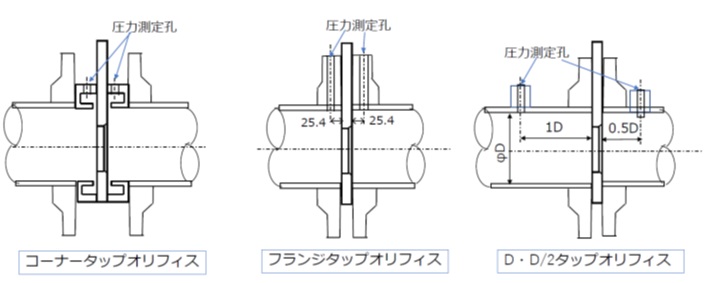
【図2 オリフィスタップの種類】
2.ベンチュリ管
オリフィスは、比較的製作が容易で価格的にも有利ですが、オリフィス下流で流れがはく離して、圧力損失が大きくなる点が短所です。(オリフィスは、絞り比を大きくして圧力損失を利用した減圧機構として使用される場合も多くあります)
一方、「ベンチュリ管」は円錐形状の絞り機構で、オリフィスに比べると圧力損失が小さく、耐摩耗性に優れている点が長所ですが、測定誤差を少なくするために高い加工精度が要求されます。
ベンチュリ管は、オリフィスに比較するとやや高価ですが、電磁流量計などに比較すれば安価で、固形物の堆積が少なく摩耗しにくいため、工業用水、工場排水など大口径の用途に適しています。
ベンチュリ管の流量計算
ベンチュリ管の場合は、オリフィスの場合のオリフィスより下流の圧力ではなく、ベンチュリ絞り最小面積部(スロート部)の圧力をp2として、ベルヌーイの定理を適用することにより、(3)式を用いて流量を求めることができます。
流量 Q=αA√(2(p1-p2)/ρ)
(Aはベンチュリ管の面積 A=πD22/4)
ベンチュリ管の流量係数αは次のようになります。
α=C/√(1-β4)
Cは「流出係数」といい、上流部とスロート部で若干のエネルギー損失が発生することの補正係数です。ベンチュリ管の材質、加工方法、管内径、絞り直径比、流速、動粘度などにより異なってきますが、一般的に0.98~0.99となります。
また、β=D2/D1で、上流部とスロート部の「絞り直径比」といいます。
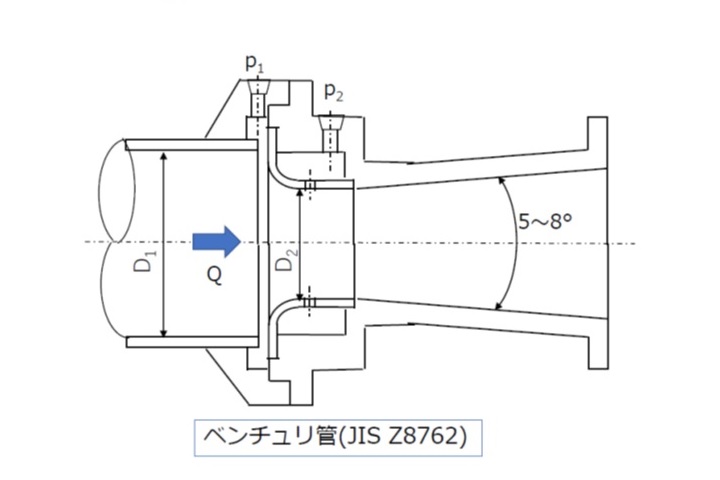
【図3 ベンチュリ管の構造】
3.ピトー管
「ピトー管」とは、流体の速度を測定するのに使用される計器です。
図4はJIS B8330に規定されている標準ピトー管で、先端に全圧測定孔、側面に静圧測定孔が設けられています。ピトー管はプロセス流量や流速の計測、風洞実験等に使われる他、飛行機の速度計測にも用いられています。
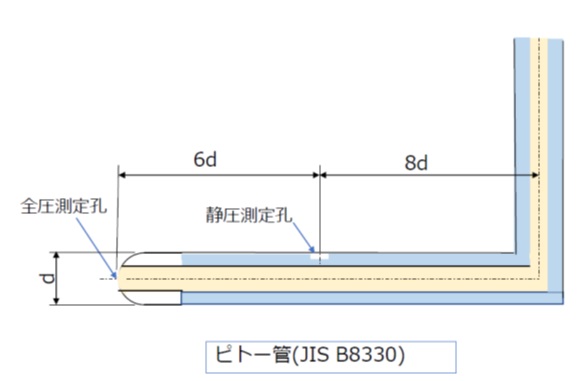
【図4 標準ピトー管の構造】
ピトー管による流速計算
図5のように、先端が丸みを帯びた円柱状の物体を流れに対向させると、流線は物体の形状に沿って滑らかに変化しますが、物体先端に向かう流線においては、物体先端の点②で流速がゼロとなります。この点を「よどみ点」といいます。
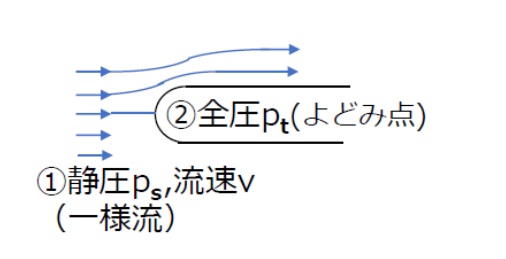
【図5 よどみ点】
上流の一様な流れ①と②に対してベルヌーイの定理を適用すると、物体が水平な流れに置かれ、位置エネルギーの変化がないとすれば、
1/2ρV12+p1=p2 ・・・(5) [※ ρ:流体の密度]
すなわち、物体先端で流れがせき止められることにより、圧力が左辺第1項の動圧1/2ρV12 の分だけ上昇することになります。
p1 は静圧であるのでこれをps と表し、p2 は動圧の分も含めた全圧になるのでこれをpt と表すことにすれば、(5)式より、流速v は
v=√(2(pt-ps)/ρ) ・・・(6)
つまり、全圧と静圧を測定すれば、流速を求めることができます。
このようにベルヌーイの定理は、流量や流速の実用的な計測に応用されています。流体を扱う機械・装置の設計等に関わる方にとって、ベルヌーイの定理を理解しておくことは極めて重要と言えるでしょう。
(日本アイアール株式会社 特許調査部 S・Y)