【機械設計マスターへの道】振動の基礎知識・重要ポイントを厳選解説（機械力学）
機械工学4力学の一つである「機械力学」は、機械の動きと、機械に働く力の大きさや方向などについて調べたり解析したりする学問です。
本コラムでは機械力学が扱う現象の中で、代表的なテーマの一つであると考えられる「振動」をとり上げます。
機械は、エネルギーを得て動くことにより、いろいろな仕事をするものです。
機械の動きには、機械が目的の仕事をするための本来の動き、すなわち平衡状態を保って仕事する位置から微小量の変位の往復を規則的に繰り返す現象が、多少なりとも伴います。これを「振動」といいます。
１．振動系と自由度、線形性
機械振動は、最も簡便には図1に示すように、質量m [kg]と、ばね定数k[N/m]のばね、からなる「ばね・質量系」として模式的に表すことができます。
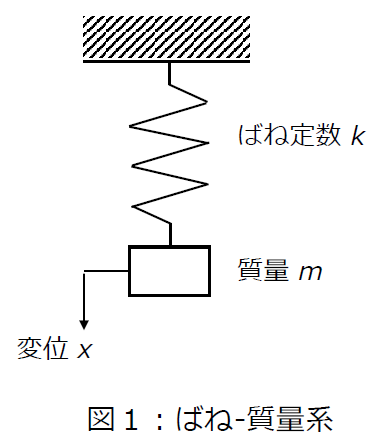
図１の系の運動方程式は、次式で表されます。
図２のように両端支持の細長いはりに質量m [kg]がついた系を考えます。
はりをシャフト、両端支持点を軸受、付加質量を羽根車とすれば、この図はポンプなどの回転機械の基本的な振動モデルです。
はり(シャフト)の縦弾性係数をE、断面二次モーメントをI、とすれば図２のモデル(質量が中央)において、シャフトのたわみに対するばね定数は、材料力学の公式よりk=48EI /L3 となります。
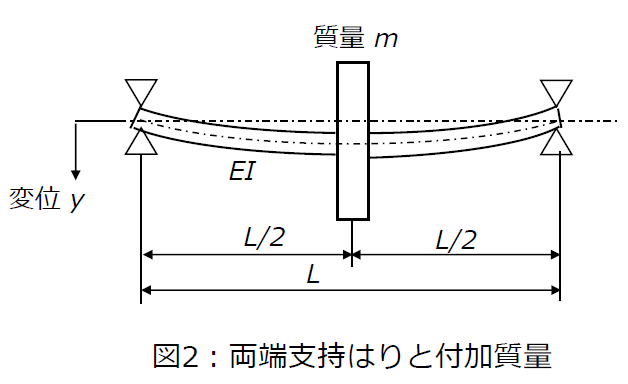
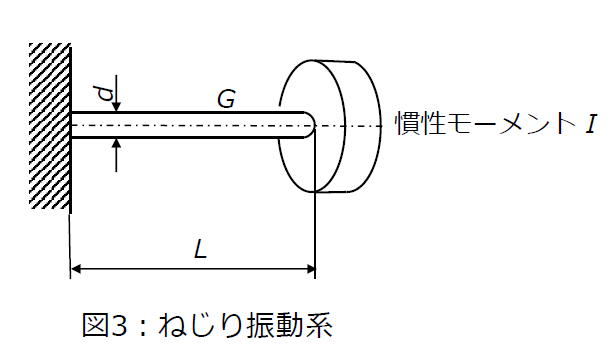
図３のように細長い軸の一端が固定され、他端に慣性モーメントI の剛体がついた振動系を考えます。
剛体にトルクTをかけたときのねじれ角をθ（シータ）とすれば、運動方程式は、次式で表されます。
駆動トルクを受ける回転機械のねじり振動の基本的なモデルです。
中実丸軸で直径d、軸材のせん断弾性係数をG とすれば、材料力学の公式より
k =πＧｄ４/32L となります。
質量・剛体の数が1つのものを「1自由度振動系」、2つあるものを「2自由度振動系」、3つ以上あるものを「多自由度振動系」といいます。
(1),(2)式の左辺第2項は、ばねの復元力を示します。
(1),(2)式のように、復元力がf(x)=kx の形で表されるものを「線形」、f(x)=αx+βx3のように変位に対して単純比例ではない特性のものを「非線形」といいます。
多自由度や非線形の振動系は、取り扱いが複雑で難解になってきます。
1自由度線形振動が基本となります。
２．振動に関連する単位
機械が一定の変位で規則的に振動するとき、平衡位置（中心）から片側変位の振れ幅を「片振幅」、両側変位の振れ幅を「両振幅」といいます。
振幅の計測には、両振幅が用いられます。単位はμm（ミクロン）P-P (Peak to Peak)です。
回転軸の動き自体の健全性を評価したいときは、両振幅計測が適しています。
振動による変位の速さを「振動速度」といいます。単位はmm/s RMSです。
”RMS”は”Root Mean Square”（二乗平均平方根）の頭文字で「実効値」とよばれ、振動波の大きさの時間平均を表します。
振動速度は振動エネルギーの大きさを表すものであり、回転軸を支える転がり軸受のハウジング上で計測し、回転体の健全性を評価する指標となります。ISOに振動診断のための振動速度評価基準が定められています。
振動速度の変化の大きさを「振動加速度」といいます。
重力加速度との比であるGが、計測単位としてよく用いられます。
振動による衝撃力の大きさを表すので、回転軸を支える転がり軸受の損傷検出などに役立ちます。
振動が正弦波状の単振動である場合、1秒間に規則的に繰り返される正弦波の数fを「振動数」、または「周波数」といいます。周波数fの単位としてHz（ヘルツ）を使用します。
ω=2πf[rad/s] を「角速度」といいます。
速度は変位の1回微分、加速度は変位の2回微分であるので、片振幅をDとしたとき、変位x、速度v、加速度aの間には次の関係があります。
- 変位 x = D sinωt
- 速度 v = Dωcosωt
- 加速度 a = -Dω2 sinωt
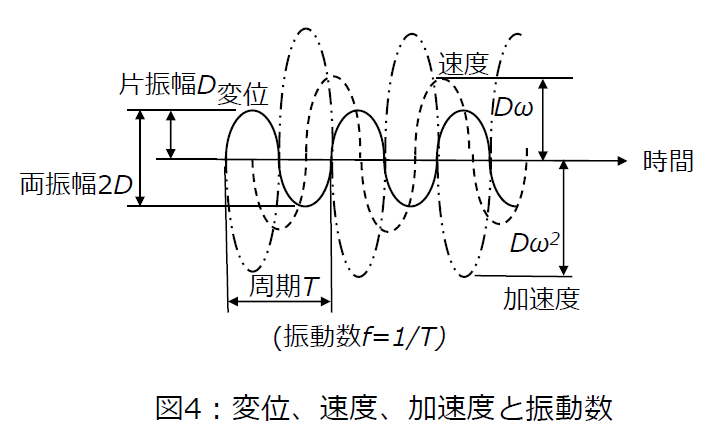
図４に、正弦波振動と、変位、速度、加速度、振動数（周波数）の関係を示します。
振動数は、周期Tの逆数です。
３．自由振動と強制振動
系に外力が作用しない場合の振動を「自由振動」、外力が作用する場合の振動を「強制振動」といいます。
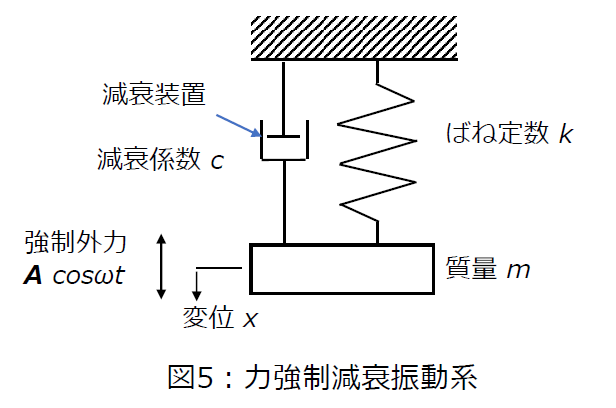
また減衰力（抵抗力）が働かない振動を「非減衰振動」、減衰力（抵抗力）が働く振動を「減衰振動」といいます。
多くの機械では、振動を抑制する抵抗力を持たせるために、図５のような「減衰装置」（ダンパー）が設けられます。
機械の振動は、何らかの外力（加振力）が作用し、かつ減衰のある「力強制減衰振動」である場合が多くあります。機械に用いられる減衰機構は、振動速度に比例する減衰特性を持つものが多く、これを「粘性減衰」といいます。（線形特性となります）
粘性減衰の振動速度比例定数を減衰係数cと表します。
図５は、力強制減衰振動モデルを示したもので、正弦波状に与えられる強制外力の片振幅をA、角速度をω、時間をt とするとき、この振動モデルは次式で表されます。
（慣性力+減衰力+復元力=外力）
４．固有振動数と共振
ここでは振動を考える上での重要な指標についてご紹介したいと思います。
固有振動数fn は、次式で表されます。
fn =(1/2π)√(k/m) ・・・（４）
系の質量とばね定数から一律に決まる値であり、ある周波数が加振されることで系が振動を起こす、系に固有の数値です。
次式で表される数を、臨界減衰係数CC といいます。
CC =2 √mk ・・・（５）
減数係数と臨界減衰係数の比C/CC をギリシャ文字ζ(ジータ)で表します。
質量 、粘性減衰 、ばね、からなる図５の系に、静的外力Aを付加したときの変位をxst、角速度（あるいは振動数）ごとの強制振動の変位をx 、x / xst を振幅倍率、といいます。
また、強制振動数の比f/fn をギリシャ文字λ（ラムダ）で表します。
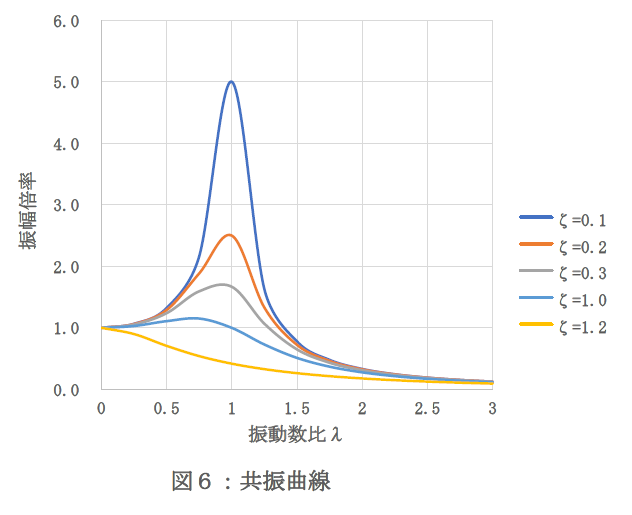
解は省略しますが（３）式より振幅倍率とλ、ζの関係を求め、図６のように横軸にλ=f/fn 、縦軸に振幅倍率x / xstをとり、ζ=C/CC をパラメータとして、図示したものを「共振曲線」といいます。
図６より、強制振動の振動数が、系の固有振動数に一致したとき、減数係数が小さい場合には、振幅倍率が増大することがわかります。これを「共振現象」といいます。
共振は多くの場合機械にとって好ましくないので、次のような対策により共振を防ぐ必要があります。
- 強制外力の振動数が、系の固有振動数から離れるように、加振源に対策を施す。（回転速度を変更する等）
- 振動系を構成する質量（軽くする、重くする）、あるいはばね定数の大きさ（硬くする、軟らかくする）を変えて、固有振動数を加振周波数から離す。
- 減衰装置の減衰を大きくする。図６よりζ>1.0となるように減衰係数を大きくすれば共振による振幅増大が起きないことがわかります。
５．危険速度
回転機械の場合、回転速度が回転体の固有値に近づくと共振現象により軸が振れ回りを起こし、軸受に過大な面圧が作用したり、内部の摺動部品が接触することで摩耗したりして健全性が損なわれ、最悪の場合には軸の折損や軸継手の破壊など重大な損傷を引き起こす場合があります。
回転体の固有値に相当する回転速度を「危険速度」といいます。
図２のように水平に設置された軸に１つの付加質量m[kg]を取付けた回転体を考えてみます。
このとき危険速度は（４）式を用いて求めることができます。
kは、回転体のたわみに対するばね定数[N/m]であり、水平に設置された主軸が静止状態で、たわみyを生ずるとき、kとyの間には次式の関係があります。
mg=kｙ ・・・(６)
（４）、（６）式より 軸の危険速度Nc[min-1]は
・・・(７)
となります。
共振を回避するため、回転速度Nが、N<0.8Ncあるいは N>1.3Ncとなるように設計します。
前者は危険速度を回転速度より十分高くする場合で「リジッドシャフト」、後者は危険速度を超えた高速回転を行う場合で「フレキシブルシャフト」といいます。
実際には、軸には段差があるなど形状変化に富んでおり、付加質量も１つではない（多自由度）場合が多く、軸受や内部摺動部品のばね特性、減衰特性を考慮するなど、危険速度の計算には複雑な過程を必要とします。
また回転機械は、軸継手を介して駆動トルクを受けて回転するものであるので、ねじれ角θが変動する回転振動を伴います。継手の慣性モーメントIと軸のねじりばね定数から求められる、系のねじり固有振動数に対する共振回避も考慮する必要があります。図３および式（２）を参照ください。
以上、機械設計を行う上で最小限必須と考えられる振動の基礎知識について簡単に紹介しました。
振動はいわば、機械がその目的を果たすための本来の動きからの逸脱ということになりますから、振動は小さいほど好ましいといえます。許容できる振動の大きさは、機械ごとに決められており、その閾値を超えて振動が大きくなると、故障の原因となったり最悪の場合には機械の破損にもつながったりします。
振動に関する文献や講習会などで更に知見を深めて、より良い機械の設計に役立ててください。
（日本アイアール株式会社 特許調査部 S・Y)
