【電気数学をシンプルに】電気分野では弧度法で![三角関数①]

交流は、電流・電圧が周期的に変化する電気です。
周期的に変動しているものが一周期のうち、どの位置にいるかを表現するために用いられるのが位相です。
位置情報なので、基準からのずれを表現する際にも位相が使われます。
位相を知りたいときは、位相角を調べる方法もあります。
(※詳細は当連載の「ベクトルと位相・位相角」のページをご参照ください。)
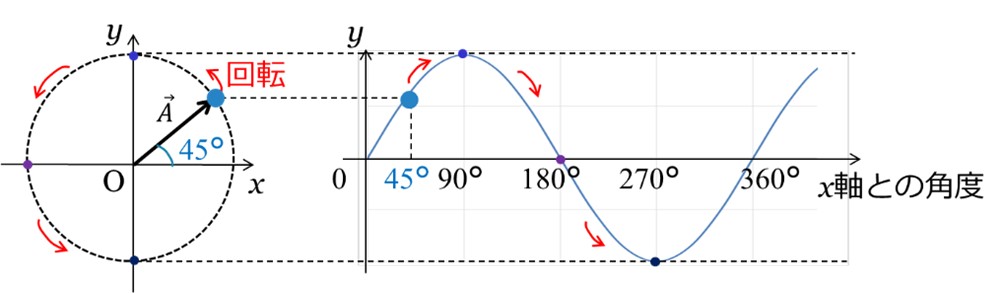
例えば、図1において、x軸との角度が0°のときを基準とすると、●の位相は45°になります。位相角は45°です。この角度を°(度)で表す方法を「度数法」といいます。
度数法は円周を360等分したときの円弧に対する中心角を1°としています。
したがって、1周は360°になります。
[図1 位相角の考え方]
交流では、計算のしやすさから、角度を「度数法」で表すよりも「弧度法」で表す方が一般的です。
交流に限らず、三角関数を扱う場合には弧度法を使うことをお勧めします。
本コラムでは、弧度法について解説します。
1.弧度法(ラジアン法)
弧度法では、円弧が半径と等しいとき、円弧に対する中心角を1[rad(ラジアン)]とします。
半径1の円(単位円)で考えると、図2のように、円弧が1のとき、1[rad]になります。

[図2 単位円における円弧と中心角の関係]
図3のように、半径r、円弧lのとき、その比 l/r は一定になります。
円弧lに対する中心角をθとすると、θは次式で定義されます。
θ=l/r
この式からわかるようにθは比なので、角度を弧度法で表現するときは通常単位[rad]をつけません。

[図3 弧度法による角度の定義]
2.角度とラジアンの対応
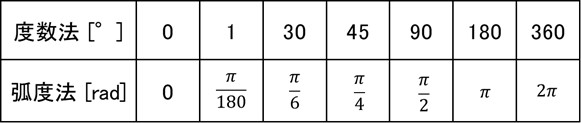
図4は、角度とラジアンの対応を表で示しています。度数法は1周を360°としています。
一方、弧度法では一周が2πになります。
[図4 角度とラジアンの対応表]
3.円弧の求め方
半径rの円周は2πrになります。したがって、図5に示すように、円弧lの大きさを度数法と弧度法で求めると以下のようになります。
度数法の場合:l = 2πr × θ/360
弧度法の場合:l = 2πr × θ/2π = rθ
このように、度数法に比べて弧度法を使うと、円弧=半径×中心角 とシンプルな式になるのがわかります。
なお、円弧を求める場合に限らず、三角関数の極限や微分積分なども扱いやすくなります。

[図5 円弧lの求め方]
以上のように、位相を表す場合には弧度法を用いて表現するのが効果的です。
正弦波交流に代表されるように、交流の波形は三角関数で表現されますので、今後、具体的に計算をしていく過程においても、弧度法で表現するありがたみを感じることと思います。
(日本アイアール株式会社 N・S)