【電気数学をシンプルに】ベクトルと位相・位相角[ベクトル/三角関数/複素数の関係①]
前回のコラム「電気数学とは?初心者が押さえておくべき前提知識を解説」では、交流波形をベクトルとして考えることができることをご説明しました。
具体的には、xy平面上で、原点Oを始点とするベクトルが原点Oを中心に反時計回りに回転したとき、そのベクトルの終点は円運動に対応していて、ベクトルの終点をy軸に投影したグラフが正弦波になることについて解説しました。
1.y=sinθとy=cosθ のグラフ(位相と位相角)
先に述べた原点Oを始点とするベクトルの大きさが1(単位ベクトル)の場合を考えます。
このとき、単位ベクトルの終点は半径1の円(単位円)を円運動します。
図1のように、水色で示した三角形の高さがそのままsinθになります。
また、三角形の底辺の大きさがcosθになります。
そして、図1のy=sinθのグラフと、図2のy=cosθのグラフを比べてみると、波形は同じで90°だけずれていることがわかります。このずれを「位相」といいます。
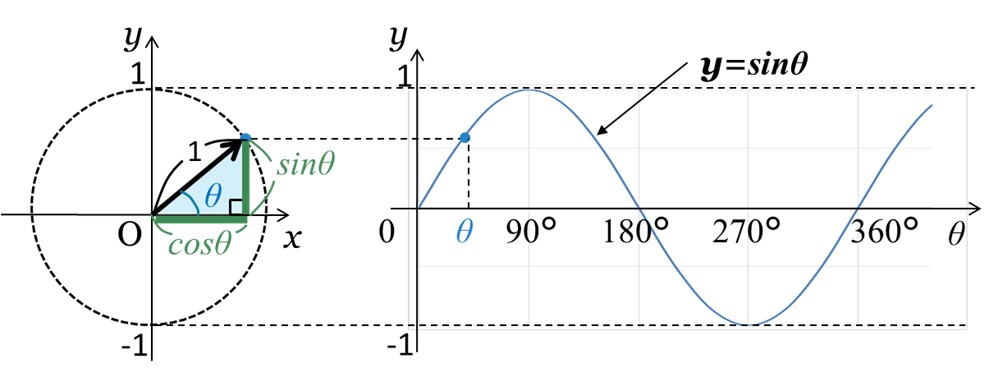
[図1 単位円におけるsinθの大きさとy=sinθのグラフ]
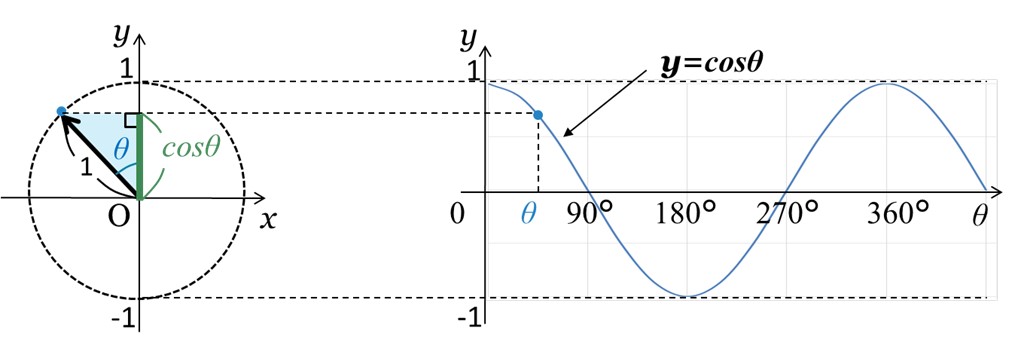
[図2 単位円におけるcosθの大きさとy=cosθのグラフ]
ここで、図3に示すように、図1における単位ベクトルと図2における単位ベクトルを比べてみると、2つのベクトルのなす角は常に90°になることがわかります。
つまり、2つのベクトルのなす角度と波形のずれとが等しくなることがわかります。
そのため、2つのベクトルのなす角度は「位相角」と呼ばれます。
また、ベクトルは、反時計回りに回転し円運動しているので、y=cosθは、y=sinθよりも位相が90°進んでいることがわかります。このように位相と位相角は対応しています。
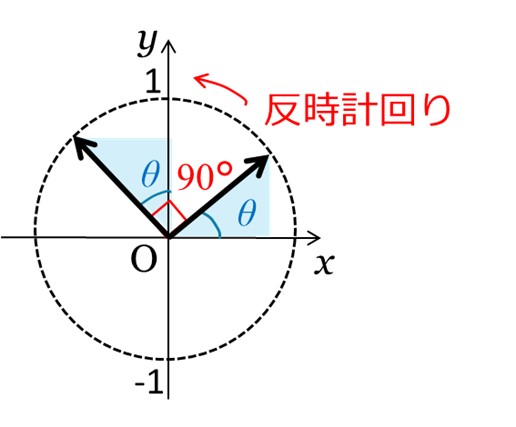
[図3 位相角]
2.位相の求め方
位相と位相角が対応するということは、位相を知りたいときには、位相角がわかればよいということです。
図4は、交流回路における波形の例を示しています。赤、緑、青の3つの波形を読み取ることができます。
実務上は、このように位相の違いや、振幅が異なる波形を目にすることがほとんどです。もっと複雑な波形に出会うこともあるかもしれません。
では、位相を求めてみましょう。
一見、波形から求めることは難しそうですが、ベクトルの位相角を調べることで簡単に求めることができます。
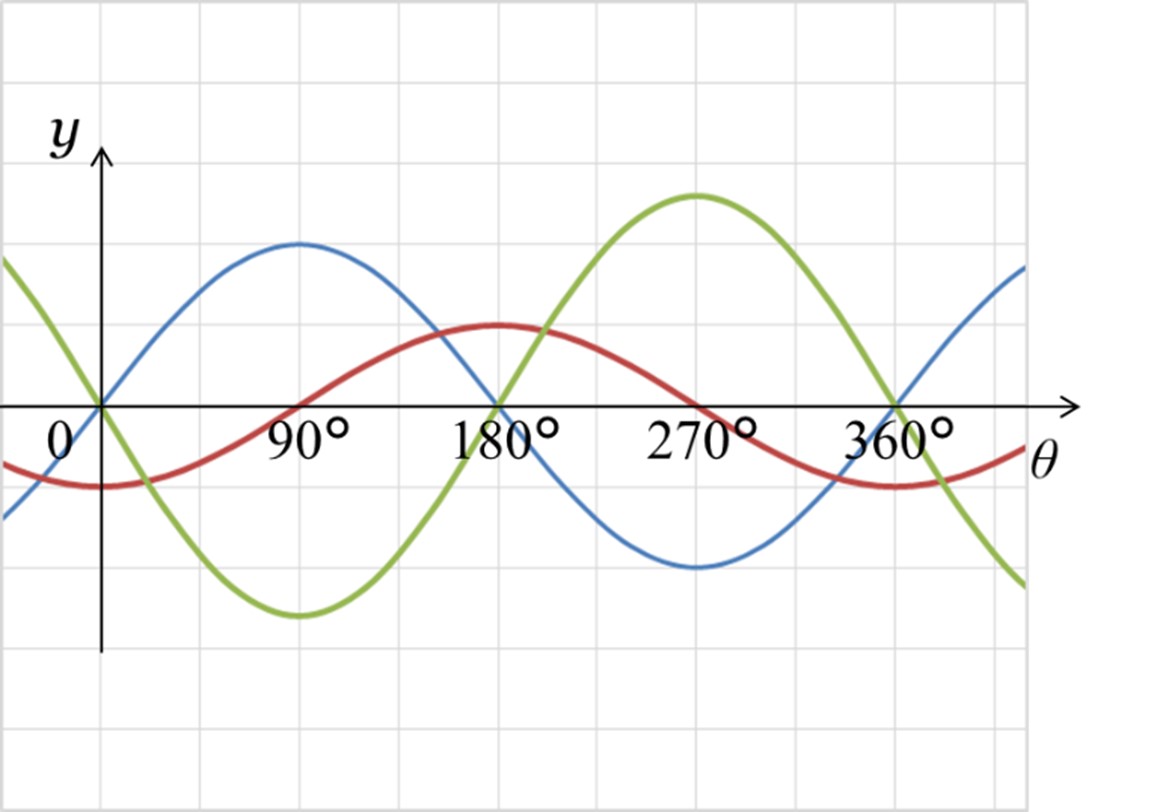
[図4 交流回路における波形の例]
図5の左側に示したように、赤、緑、青の波形について振幅に等しい円を考えます。
ベクトルの大きさは、電圧や電流の最大値になります。
そして、グラフに対応するベクトルをそれぞれ作成すると、ベクトル間の角度が位相になります。
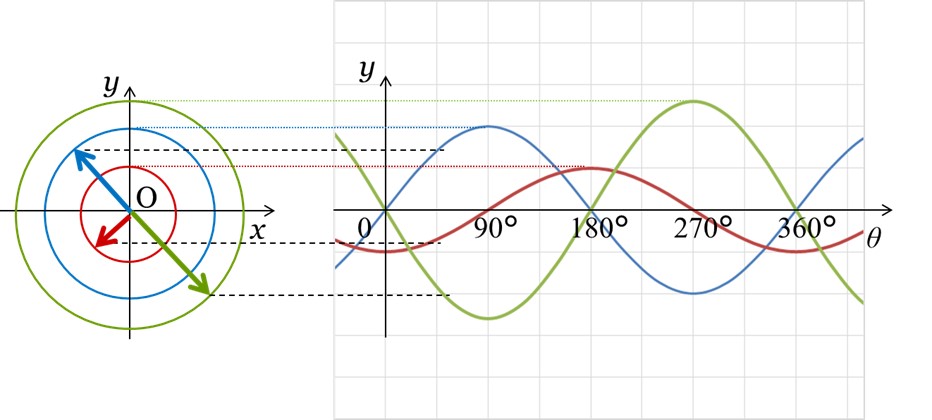
[図5 回転ベクトルと正弦波]
以上、今回は位相と位相角の基本について解説しました。
次回は、RLC直列回路を題材として、ベクトルの使い方を説明します。
(日本アイアール株式会社 N・S)