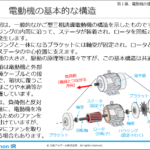
3分でわかる 希土類金属(レアアース)の発光原理

希土類元素(レアアース)は、殆どが4f軌道に不対電子をもっています。
前回のコラム「希土類金属(レアアース)と磁性」では、この不対電子の働きによる磁性体への応用についてご紹介しました。
不対電子は、光や電気などのエネルギーで励起して、他の軌道に一時的に移ることができます。
そして、元の軌道に戻るときにもらったエネルギーを光として放出すると、発光となります。
今回のコラムでは、希土類金属の基本的な発光原理を解説します。
1.角運動
周期表に118種類の元素がありますが、発光する元素は主にランタノイド(レアアース)と第一遷移元素(原子番号21のScから29のCu)に集中しています。
これらの元素に共通するのは内殻軌道に不対電子をもつことです。
4f軌道の電子配置は表1をご参照ください。
なお、Sc3+、Y3+ とLa3+はf電子を持たず、Lu3+は7つの軌道が全て2個のペア電子で埋まっており、不対電子がないので表に載せていません。
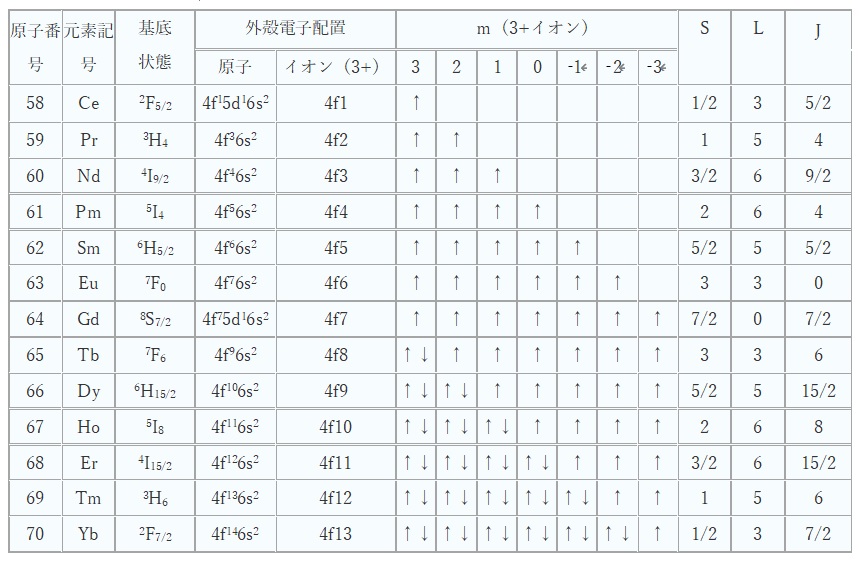
【表1 希土類元素の電子配置と量子化学データ】
磁気量子数m、スピン角運動量S、全軌道角運動量L、全角運動量J
発光を考えると、軌道の分裂やエネルギー準位は避けて通れない量子化学課題です。
ここでまず「角運動」について説明します。
表1の「基底状態」とは、電子配置が最もエネルギーの低い電子配置のことをいいます。
電子の状態を表すために、まず磁気量子数mとS、L、Jの角運動量を説明します。
ご存じのように、4fには7つの軌道があり、それぞれ違う方位に向きます。
各軌道の角運動量について、XYZ軸上のZ成分の違いを示す磁気量子数mは、それぞれ3, 2, 1, 0, -1, -2, -3で区別します。Hundの規則(※後述)に従って、CeからGdにかけて、これらの軌道に上向きスピンの電子が磁気量子数mの大きい方から1個ずつ入っていきます。Gdで不対電子7個であり、半充填となります。
TbからYbにかけては、下向きスピンの電子が入りペアを作っていくので、不対電子の数は減少していき、Ybの不対電子は1個になります(表1)。
スピン角運動量
Sは「スピン角運動量」といい、電子向きの違いによって+1/2(上向き)、-1/2(下向き)で表して、複数電子の場合はスピンの和となります。
例えば、Nd3+は上向きのスピン3個で、S=(+1/2)x3=3/2、
Er3+は上下逆の電子対は4つで(+1/2+(-1/2)=0)、
上向きの不対電子3個なので、S=(+1/2)x3 =3/2
となります。
全軌道角運動量
Lは「全軌道角運動量」といい、1電子の軌道角運動量 Lを組み合わせたものです。
その組み合わせ方は、Lをベクトルとして、そのベクトルの和によって考えられます。
計算方法は磁気量子数mの和です。
Nd3+の場合、m=3、2、1に1コずつの不対電子があるので、
L=3+2+1=6、
Er3+はm=-1, -2, -3に3つの不対電子があるので、
L=∣(-1)+(-2)+(-3)∣=6となります。
Lの値に対応して、記号で表します。
Nd3+ とEr3+ の場合、Lの記号はIです(式1)。
L: 0, 1, 2, 3, 4, 5, 6・・・
記号:S, P, D, F, G, H, I・・・ 式1
全角運動量
Jは「全角運動量」といい、全軌道角運動量Lとスピン角運動量Sを合成したものです。
合成の方法は、CeからEuまでの軽希土類ではJ=L-S、GdからYbまでの重希土類ではJ=L+Sになります。
例えば、NdではJ=6-3/2=9/2、ErではJ=6+3/2=15/2です。
2.電子項記号の意味と表示方法
表1の基底状態の欄にある記号は「スペクトル項」あるいは「項記号」と呼ばれ、式1の形で表します。
左上の数字 2S+1 はスピン多重度の意味で、例えば S=1 だと3になり、3重に縮重した状態で、スピン軌道相互作用により3つに分裂することが分かります。右下は全角運動量Jで、縮重は(2J+1)となります。
例えば、L=2、S=1の場合は、3D1、3D2、3D3と表示して、この一つ一つの組み合わせを電子項と呼びます。
2S+1LJ 式2
表1の基底状態のNd3+とEr3+の場合を考えると、それぞれ4I9/2と4I15/2となります。
3.フントの規則(フントの法則)
フント(Hund)の規則は、エネルギー準位図において、軌道を安定な軌道から並べる際の重要な規則です。
一般的なエネルギー準位図では、安定な軌道が下に描かれます。
以下のルールによって、安定準位が決められます。
- スピン多重度の最も大きな項は安定。
(例:3Dより5Dが安定) - スピン多重度が最大の項が複数あるときは、全軌道角運動量Lが大きい項が安定。
(例:3Pより3Fが安定) - スピン多重度と全軌道角運動量が同じ場合は、
3-1.準殻の電子が半分以下の場合、Jが小さい項が安定。
(例:4F2より4F1が安定)
3-2.準殻の電子が半分以上の場合、Jが大きい項が安定。
(例:7F5より7F6が安定)
4.発光のエネルギー準位図
希土類イオンの発光は、軌道の分裂や電子遷移によって複雑となります。
細かい軌道分裂を省略すると分かりやすくなります。
図1に示したように、Er3+軌道間のエネルギー差に合った波長(980nm)の光を照射すると基底状態(4I15/2)の4f電子が上位準位4I9/2へ励起されます。
励起された電子は非発光で 4I13/2 へ遷移したあと、波長1550nmの光を放出して、基底状態に戻ります。
また、Er3+は、1480nmの光で 4I13/2 へ直接励起して発光させることも可能です。
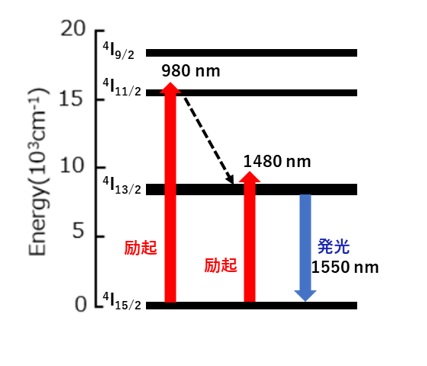
【図1 Er3+の発光とエネルギー準位図】
以上、今回はレアアースの発光原理についてご紹介しました。
(日本アイアール株式会社 特許調査部 H・L)