【電気数学をシンプルに】複素数と微分・積分
本連載においては、複素数を使うことで計算が楽になるケースをいくつか説明してきました。
今回は、複素数と微分・積分との関係について解説します。
１．微分と積分
はじめに、微分と積分のイメージを確認しておきたいと思います。
微分（differential）とは、微分係数を求めることをいいます。つまり、図1左に示されるグラフ上の任意の点における接線の傾きを調べることが微分です。また、導関数を求めることも微分と呼ばれます。
一方、積分（Integral）とは、図1右に示されるように、曲線や曲面で囲まれる領域を細分化して領域の面積を近似することをいいます。
交流回路を解析するときには、微分と積分を含む式を解いていくことが必要になる場合があります。
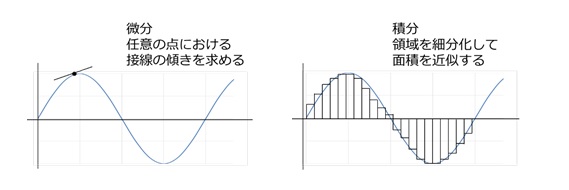
［図1 微分と積分のイメージ（左が微分、右が積分）］
２．複素数と微分の関係（RL直列回路）
図2は、抵抗Rと 自己インダクタンスLのコイルを、直列に接続したRL直列回路です。
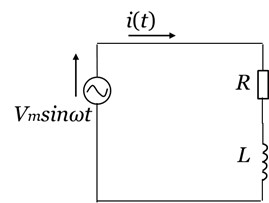
［図2 RL直列回路］
交流回路において、瞬時値である電圧や電流は以下の式で表すことができます。
オイラーの公式(*)より、
であるから、
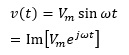
となります。
［(*)オイラーの公式に関する解説はこちらのページをご参照下さい。］
ここで、
![Im[e^jωt ]](https://engineer-education.com/wp/wp-content/uploads/2021/10/Eulerss-formula-3.jpg){kind=small}
は、Vmejωtの虚部のみをとりだすことを意味します。
また、抵抗Rに流れる電流i(t)は、オームの法則より
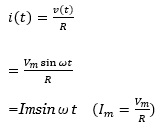
になります。
コイルの端子電圧vL(t)は、
になります。
RL直列回路においては、次式が成り立ちます。
ここで、
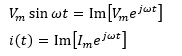
を代入すると、
また、
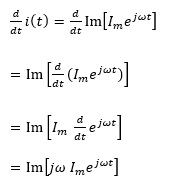
（↑ejωtを微分することは、jωをかけることに置き換えることが可能）
であるから、
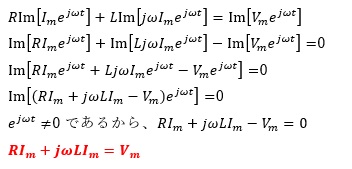
Imについて解くと、
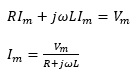
さて、先に記述した赤字で示した2式を比較してみると、
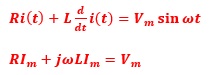
次のように置き換えが可能であることがわかります。
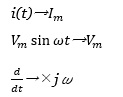
３. 複素数と積分の関係（RC直列回路）
積分についても微分のように式の置き換えができます。
図3は、抵抗Rと コンデンサCを直列に接続したRC直列回路を示します。
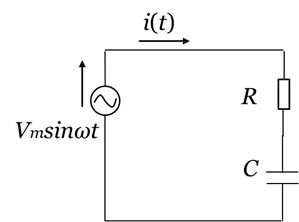
［図3 RC直列回路］
コンデンサの端子電圧vC(t)は、
になりますので、RC直列回路においては、次式が成り立ちます。
ここで、
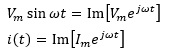
を代入すると、
また、
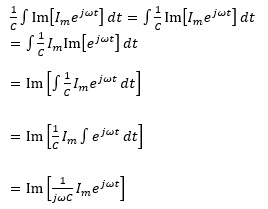
であるから、
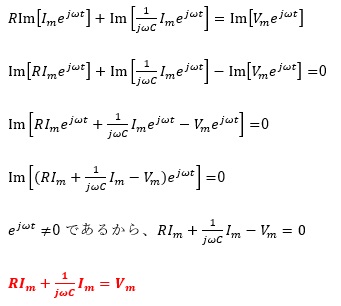
さて、先に記述した赤字で示した2式を比較してみると、
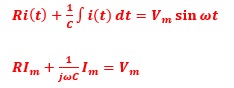
次のように置き換えが可能であることがわかります。
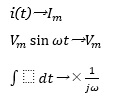
４．複素数を使ってラクに解く！
交流回路においては、未知数を求める場合に微分や積分を含む式を解く必要があります。
そのままでも解けないことはありませんが、複素数を使うことで微分方程式を代数方程式に置き換えることができ、楽に解いていくことができます。
本連載で紹介したことがきっかけとなり、少しでも電気回路・電子回路についての理解が深まれば幸いです。
（日本アイアール株式会社 N・S)
