【電気数学をシンプルに】電気回路の解析③ 逆行列と行列式
今回のコラムでは、行列を計算する方法として、逆行列について解説します。
行列では除算が定義されていません。
ただし、除算に相当する演算としてイメージできる「逆行列」が定義されています。
(*行列の加算、減算、乗算については「電気回路の解析② 行列の演算方法をチェック」をご覧ください。)
目次
1.逆行列とは?
「逆行列」とは、ある行列とかけ算すると単位行列Eになる行列です。
つまり、行列Aと逆行列A-1との関係は以下の式で表されます。
A-1A=AA-1=E
行列Aと行列Bの積は、一般に可換性がなくAB≠BAになりますが、ある行列Aとその逆行列A-1との積は可換性があります。
2.逆行列の求め方
(1)1×1行列の場合
逆行列A-1は、その成分とします。
A=(1)のとき、
A-1=(1)になります。
(2)2×2、3×3行列の場合
逆行列A-1は、行列式detAの逆数と余因子行列adjAの積になります。
そのため、行列式detAが0のときは、逆行列A-1が存在しません。
(行列式と余因子行列については後半で説明しています。)
![]() ただし、detA≠0
ただし、detA≠0
![]() のとき、
のとき、
detA=ad-bc、 adjA= ![]() を代入し、
を代入し、
![]() ただし、ad-bc≠0 となります。
ただし、ad-bc≠0 となります。
 のとき、
のとき、
detA = a11(a22a33 -a23a32) -a12(a21a33 -a23a31) +a13(a21a32 -a22a31)

を代入して計算します。
3.行列式(determinant)
先ほど、逆行列A-1を求める際に用いた「行列式」とは、行数と列数が等しいn×n行列において定義されるスカラです。ここでは、行列式の求め方について説明します。
(1)1×1行列の場合
行列式はその成分とします。
A=(1)のとき、
detA=1になります。
(2)2×2行列の場合
![]() のとき、
のとき、
![]()
= ad -bc
(3)3×3行列の場合
 のとき、
のとき、
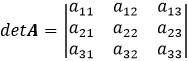
= a11A11 -a12A12 +a13 A13(A11、A12、A13は部分行列です。後ほど説明しています。)
![]()
= a11(a22a33 -a23a32) -a12(a21a33 -a23a31) +a13(a21a32 -a22a31)
4.余因子と余因子行列(adjoint matrix)
3×3行列の逆行列A-1を求める際に「部分行列を使いました。
「部分行列」とは、行列Aのi行またはj列以外の成分からなる行列をいいます。
また、行列Aのi行とj列以外の成分からなる部分行列Aijの行列式に (-1)i+j をかけたものを「余因子」といいます。
余因子 (-1)i+j ×detAij
この余因子を成分とする行列が「余因子行列(adjoint matrix)」になります。
余因子と余因子行列adjAの求め方は以下の通りです。
- 行列Aのi行とj列以外の成分からなる部分行列Aijをつくる
- 各部分行列Aijの行列式detAijを求める
- 求めた行列式detAijに(-1)i+jをかけて余因子を求める
- 余因子を成分とする行列(余因子行列)をつくる
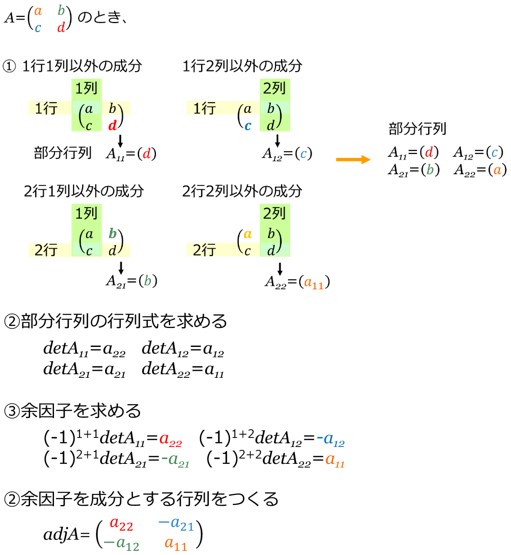
(1)2×2行列における余因子行列の求め方
図1に示したように、
![]() のとき、
のとき、
adjA=![]() になります。
になります。
(2)3×3行列における余因子行列の求め方
図2に示したように、
 のとき、
のとき、
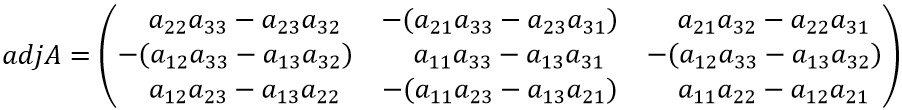
になります。



ということで今回のコラムでは、逆行列の求め方について解説しました。
3×3行列の逆行列の求め方については、ここで紹介した以外にもいくつかの方法がありますが、応用のしやすさを考慮して余因子を用いた方法を取り上げました。
次回の連載コラム「キルヒホッフの法則と行列法」では、実践的な問題も用意しています。
ぜひ取り組んでみてください。
(日本アイアール株式会社 N・S)













](https://engineer-education.com/wp/wp-content/uploads/2021/10/electric-circuit-dc0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2022/08/elearning_AC-circuit1_0-150x150.png)
](https://engineer-education.com/wp/wp-content/uploads/2022/08/elearning_AC-circuit_0-150x150.png)
































