【電気数学をシンプルに】電気回路の解析① 行列の基本《連立一次方程式を行列法で解く》

電気回路の解析では、未知数を求めるために連立方程式を解くことがあります。
本コラムでは、連立方程式を解く方法の1つである行列法について解説します。
1.行列の基本(行と列、単位行列、逆行列)
(1)行列の行と列、成分
「行列」とは、数などを縦と横に配列したものをいいます。
横の並びが行で、縦の並びが列になります。「行数×列数」で行列を呼ぶこともあります。
例えば、図1に示すように、2行で1列から成る行列は、「2×1行列」になります。

[図1 行列における行と列]
また、行列を構成している数字などを「成分」といいます。
図1の行列では、1行1列の成分がxで、2行1列の成分がyです。
(2)単位行列
「単位行列En」とは、行数と列数が等しいn×n行列(正方行列)において、n行n列成分が1であり、その他の成分が0である行列です。
n=2、すなわち、2×2行列の場合、単位行列は、
![]()
になります。
(3)逆行列
「逆行列」とは、ある行列とかけ算すると単位行列Enになる行列です。
つまり、行列Aと逆行列A-1との関係は以下の式で表されます。
A-1A=AA-1=En
例えば、![]() のとき、
のとき、
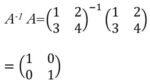
が成り立つ
![]()
が逆行列A-1です。
逆行列は、次のように求めることができます。
(※詳しくは、今後の当連載「電気回路の解析③ 行列の演算 逆行列と行列式」で解説予定です。)
![]()
ただし、detA≠0
ここで、detAは、行列式と呼ばれ以下のように計算します。(*)
![]()
=1×4-2×3
=-2
したがって、
![]()
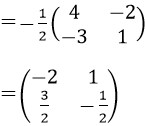
(*)行列式は、行数と列数が等しいn×n行列Aにおいて定義され、その行列式の値は、2×2行列の場合、次式で求めることができます。
![]()
=ad-bc
2.連立一次方程式と行列法
未知数を含む等式を方程式といい、複数の方程式の組み合わせたものを連立一次方程式といいます。
例えば、次式が連立一次方程式になります。
![]()
未知数x、yの求め方には、加減法や代入法と呼ばれる方法がありますが、ここでは、行列を用いた方法(行列法)を紹介します。
まず、連立一次方程式
![]()
を行列で表すと以下のようになります。
![]()
両辺に左から逆行列をかけます。
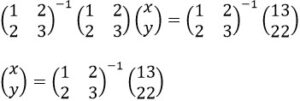
ここで、逆行列 ![]() を計算します。
を計算します。
まず、行列式の値を求めます。
![]()
=1×3-2×2
=-1
よって、
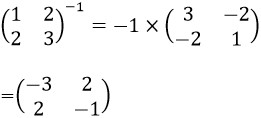
したがって、
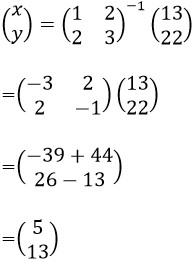
以上より、x=5、y=13の解が得られます。
3.まずは行列法に慣れること
連立方程式を解く方法の1つである行列法について解説しましたが、まずは、2×2行列を用いた方法に慣れることが必要です。行列法は未知数が多いときにその効果を発揮しますので、3×3行列を用いた行列法についても別途ご紹介する予定です。
次回の連載では、行列の演算方法の基本を解説します。
(日本アイアール株式会社 N・S)