デジタル回路のエンコーダとデコーダが基礎からわかる!

デジタル回路は、論理回路とも呼ばれていますが、論理回路のうち入力信号の組み合わせだけで出力が決まるような論理回路を「組み合わせ回路」と呼びます。
この「組み合わせ回路」のうち、今回は「エンコーダ」と「デコーダ」について説明します。
1.エンコーダとは? デコーダとは?
デコーダについては、当連載の「組み合わせ回路を基礎から学ぶ」の回でも取り上げましたが、エンコーダとデコーダは対になっていることが多いので、改めて説明します。
コンピュータで様々な処理をする場合、私達が日常使用している10進数のデータを2進数のデータに変換する必要があります。このような目的で使われる組み合わせ回路を「エンコーダ」(encoder:符号器)といいます。
逆に、コンピュータで処理された2進数のデータを10進数のデータへ変換する組み合わせ回路を「デコーダ」(decoder:復号器)といいます。

【図1 電源回路の分類(出力での分類)】
例えば、図1のようにコンピュータで情報処理する場合に、10進数の入力データをコンピュータで扱いやすい2進数に変換する部分が「エンコーダ」で、情報処理した後の2進数を人間が理解しやすい10進数に変換する部分が「デコーダ」となります。
2.エンコーダの回路
ここでは、エンコーダの例として、10進数を2進数に変換する回路を見てみましょう。
例えば、10進数の0から7の8つの数字について、8入力(A0、A1、A2、A3、A4、A5、A6、A7)のいずれか 1つが 値 1をとるものとして、それらの2進数に対応する3ビットの 出力(Z0、Z1、Z2)を生成するエンコーダを考えます。(図2)
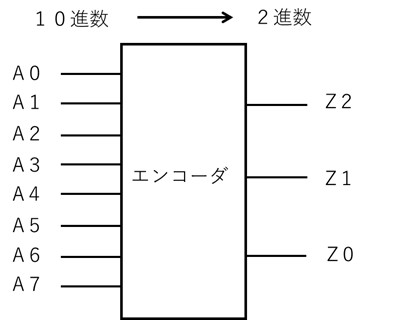
【図2 エンコーダのイメージ】
まず、8入力3出力の真理値表を作成してみます。
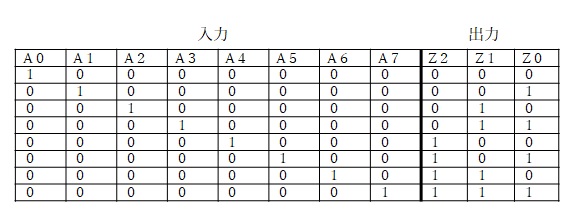
【図3 エンコーダの真理値表の例】
図3は、8入力3出力の真理値表を示す図です。
A0からA7に、10進数の0から7の8つの数字を当てはめると、出力に2進数の値が(Z2、Z1、Z0)で示されます。
例えば、A1=1ならば、(Z2、Z1、Z0)=(0、0、1)とか、A7=1ならば、(Z2、Z1、Z0)=(1、1、1)が得られます。これを回路図で示すと、図4になります。
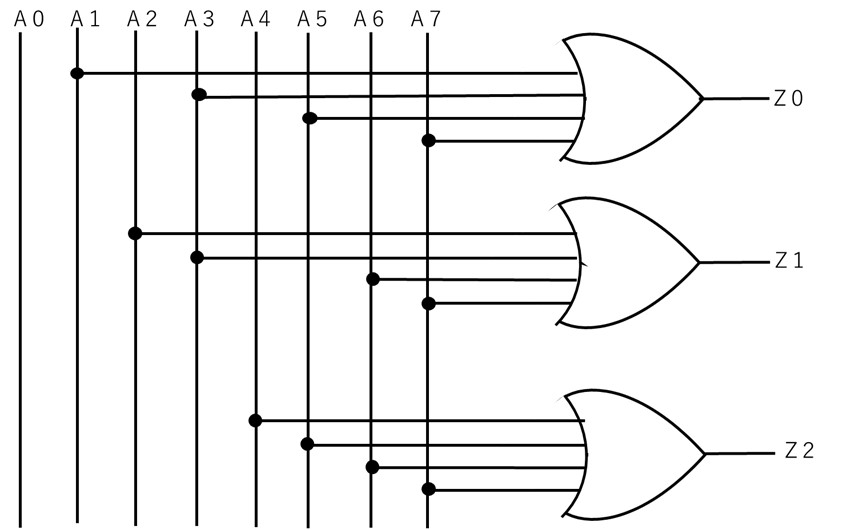
【図4 エンコーダの回路図の例】
すなわち、図2に示しているエンコーダの中は、図4のような回路になっています。
3.デコーダの回路
デコーダは、入力を判定して該当する出力を1にする「組み合わせ回路」です。
ここでは、エンコーダの反対に2進数を10進数に変換する回路を考えてみましょう。
まず、図2のエンコーダの逆で、2進数の入力(A2、A1、A0)から、10進数の0から7の8つの数字に対応する出力(Z0、Z1、Z2、Z3、Z4、Z5、Z6、Z7)のいずれか1つが、値 1をとるようなデコーダを考えます。
真理値表を作ってみると、図5のようになり、図3と逆の真理値表になります。
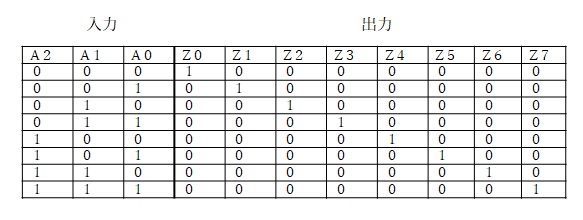
【図5 デコーダの真理値表の例】
図5の真理値表から3つの入力信号(A2、A1、A0)によって、8つの出力信号(Z0、Z1、Z2、Z3、Z4、Z5、Z6、Z7)のいずれかに1が出力されることがわかります。
Z0からZ7を10進数の0から7に対応させると、2進数を10進数に変換していることがわかります。
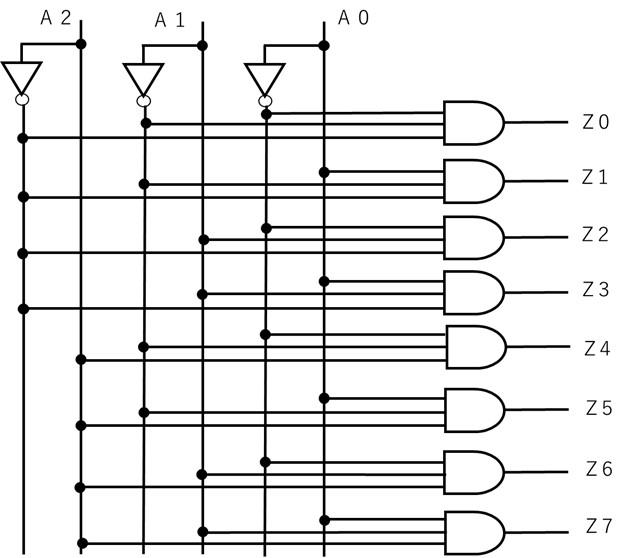
【図6 デコーダの回路図の例】
図6は、図5の真理値表を回路図にしたものです。
図6において、例えば、(A2、A1、A0)=(0、0、0)の時は、いずれもNOT回路を通って反転され1になり、AND回路を通っているのでZ0には1が出力されます。
そして、(A2、A1、A0)=(0、0、0)以外の時は、Z0には0が出力されます。
同様にして、図5の真理値表のような入力と出力の関係になります。
以上、今回はエンコーダとデコーダについて解説しましたが、これらの部分は、コンピュータと人間をつなぐ(マンマシンインターフェース)重要な回路といえます。
(日本アイアール株式会社 特許調査部 E・N)















](https://engineer-education.com/wp/wp-content/uploads/2021/10/Circuit-element0-150x150.png)































